Теорема Ролля

Если действительная функция $f$ непрерывна ( на замкнутом интервале $[a, b]$ , дифференцируема на открытом интервале $(a, b)$ и $f, то a) = f (b)$ существует $c$ на открытом интервале $(а, б)$ такой, что $ж'(c) знак равно 0$ .

В исчислении , теорема Ролля или лемма Ролля по существу утверждают, что любая вещественнозначная дифференцируемая функция которая достигает равных значений в двух различных точках, должна иметь по крайней мере одну точку где-то между ними, в которой наклон касательной линии равен нулю. Такая точка известна как стационарная точка . Это точка, в которой первая производная функции равна нулю. Теорема названа в честь Мишеля Ролля .

Стандартная версия теоремы

Если действительная a функция $f$ непрерывна ( собственном замкнутом интервале $[a, b]$ , дифференцируема на открытом интервале $(a, b)$ и $f, то на) = f (b)$ существует хотя бы один $c$ в открытый интервал $(a, b)$ такой, что $f'(c)=0.$

Эта версия теоремы Ролля используется для доказательства теоремы о среднем значении , частным случаем которой действительно является теорема Ролля. Это также является основой доказательства теоремы Тейлора .

История

Хотя теорема названа в честь Мишеля Ролля , доказательство Ролля 1691 года охватывало только случай полиномиальных функций. В его доказательстве не использовались методы дифференциального исчисления , которые на тот момент своей жизни он считал ошибочными. Теорема была впервые доказана Коши в 1823 году как следствие доказательства теоремы о среднем значении . ^{[ 1 ]} Название «теорема Ролля» впервые было использовано Морицем Вильгельмом Дробишем из Германии в 1834 году и Джусто Беллавитисом из Италии в 1846 году. ^{[ 2 ]}

Примеры

Первый пример

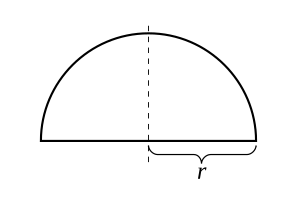
Для радиуса $r > 0$ рассмотрим функцию $f(x)={\sqrt {r^{2}-x^{2}}},\quad x\in [-r,r].$

Его график представляет собой верхний полукруг с центром в начале координат. Эта функция непрерывна на замкнутом интервале $[- r, r]$ и дифференцируема на открытом интервале $(- r, r)$ , но не дифференцируема в конечных точках $— r$ и $r$ . Поскольку $f (- r) = f (r)$ применима теорема Ролля, и действительно, существует точка, в которой производная $f$ равна нулю. Теорема применима даже тогда, когда функцию нельзя дифференцировать в конечных точках, поскольку она требует, чтобы функция была дифференцируемой только на открытом интервале.

Второй пример

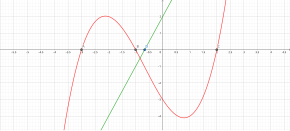
Если дифференцируемость невозможна во внутренней точке интервала, вывод теоремы Ролля может не выполняться. Рассмотрим абсолютного значения функцию $f(x)=|x|,\quad x\in [-1,1].$

Тогда $f (-1) = f (1)$ , но между −1 и 1 не существует $c,$ для которого $f'(c)$ равно нулю. Это связано с тем, что эта функция, хотя и непрерывна, не дифференцируема в точке $x = 0$ . Производная $f$ меняет знак при $x = 0$ , но не достигает значения 0. Теорема не может быть применена к этой функции, поскольку она не удовлетворяет условию, согласно которому функция должна быть дифференцируемой для каждого $x$ в открытом интервале. Однако, когда требование дифференцируемости исключено из теоремы Ролля, $f$ по-прежнему будет иметь критическое число в открытом интервале $(a, b)$ , но может не давать горизонтального тангенса (как в случае абсолютного значения, представленного на графике ).

Обобщение

Второй пример иллюстрирует следующее обобщение теоремы Ролля:

с действительным знаком $Рассмотрим непрерывную функцию f$ на замкнутом интервале $[a, b]$ с $f (a) = f (b)$ . Если для каждого $x$ в открытом интервале $(a, b)$ правый предел $f'(x^{+}):=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(x)}{h}}$ и левый предел $f'(x^{-}):=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(x)}{h}}$

существуют в расширенной вещественной прямой $[-\infty, \infty]$ существует некоторое число $c$ , то в открытом интервале $(a, b)$ такое, что один из двух пределов $f'(c^{+})\quad {\text{and}}\quad f'(c^{-})$ ≥ $0$ , а другой $\leq 0$ (в расширенной вещественной прямой). Если правый и левый пределы совпадают для каждого $x$ , то они совпадают, в частности, для $c$ , следовательно, производная $f$ существует в точке $c$ и равна нулю.

Примечания

Если $f$ выпуклое или вогнутое, то правая и левая производные существуют в каждой внутренней точке, следовательно, указанные выше пределы существуют и являются действительными числами.
Этой обобщенной версии теоремы достаточно, чтобы доказать выпуклость , когда односторонние производные монотонно возрастают : ^{[ 3 ]} $f'(x^{-})\leq f'(x^{+})\leq f'(y^{-}),\quad x<y.$

Доказательство обобщенной версии

Поскольку доказательство стандартной версии теоремы Ролля и ее обобщения очень похожи, мы докажем это обобщение.

Идея доказательства состоит в том, чтобы доказать, что если $f (a) = f (b)$ , то $f$ должна достигать либо максимума, либо минимума где-то между $a$ и $b$ , скажем, в точке $c$ , и функция должна измениться с возрастающей на убывающую ( или наоборот) в $c$ . В частности, если производная существует, она должна быть равна нулю в точке $c$ .

По предположению, $f$ непрерывен на $[a, b]$ и по теореме об экстремальных значениях достигает как максимума, так и минимума в $[a, b]$ . Если они оба достигаются в конечных точках $[a, b]$ , то $f$ является постоянным на $[a, b]$ и поэтому производная $f$ равна нулю в каждой точке из $(a, b)$ .

Предположим тогда, что максимум получен во внутренней точке $($ c $a, b) ($ аргументация минимума очень похожа, просто рассмотрим $- f$ ). Мы рассмотрим указанные выше правые и левые пределы отдельно.

Для реального $h$ такого, что $c + h$ находится в $[a, b]$ , значение $f (c + h)$ меньше или равно $f (c),$ потому что $f$ достигает своего максимума в $c$ . Следовательно, для каждого $h >$ 0 ${\frac {f(c+h)-f(c)}{h}}\leq 0,$ следовательно $f'(c^{+}):=\lim _{h\to 0^{+}}{\frac {f(c+h)-f(c)}{h}}\leq 0,$ где предел существует по предположению, он может быть минус бесконечность.

Аналогично, для каждого $h < 0$ неравенство меняется, потому что знаменатель теперь отрицательный, и мы получаем ${\frac {f(c+h)-f(c)}{h}}\geq 0,$ следовательно $f'(c^{-}):=\lim _{h\to 0^{-}}{\frac {f(c+h)-f(c)}{h}}\geq 0,$ где предел может быть плюс бесконечность.

Наконец, когда указанные выше правый и левый пределы совпадают (в частности, когда $f$ дифференцируема), тогда производная $f$ в точке $c$ должна быть равна нулю.

(В качестве альтернативы мы можем напрямую применить теорему Ферма о стационарной точке .)

Обобщение на высшие производные

Мы также можем обобщить теорему Ролля, потребовав, чтобы $f$ имело больше точек с одинаковыми значениями и большей регулярностью. В частности, предположим, что

функция $f$ n $на - 1$ раз непрерывно дифференцируема замкнутом интервале $[a, b]$ , и $n$ -я производная существует на открытом интервале $(a, b)$ , и
существует $n$ интервалов, заданных $a 1 < b 1 \leq a 2 < b 2 \leq \dots \leq a n < b n$ в $[a, b]$ таких, что $f (a k) = f (b k)$ для каждого $k$ от 1 до $н$ .

Тогда существует число $c$ в $(a, b)$ такое, что $n$ -я производная от $f$ в точке $c$ равна нулю.

Требования, касающиеся $n-$ й производной $f,$ можно ослабить, как в приведенном выше обобщении, давая соответствующие (возможно, более слабые) утверждения для правых и левых пределов, определенных выше с помощью $f (п - 1)$ вместо $ф$ .

В частности, эта версия теоремы утверждает, что если функция, дифференцируемая достаточное количество раз, имеет $n$ корней (поэтому они имеют одно и то же значение, то есть 0), то существует внутренняя точка, в которой $f (п - 1)$ исчезает.

Доказательство

В доказательстве используется математическая индукция . Случай $n = 1$ — это просто стандартная версия теоремы Ролля. Для $n > 1$ примем в качестве предположения индукции, что обобщение верно для $n - 1$ . Мы хотим доказать это для $n$ . Предположим, что функция $f$ удовлетворяет условиям теоремы. стандартной версии теоремы Ролля для каждого целого числа $k$ от 1 до $n$ существует $ck .$ открытом интервале $(ak По, bk 0)$ такой, что $f (ck в) =$ ′ Следовательно, первая производная удовлетворяет предположениям о $n - 1$ замкнутых интервалах $[c 1, c 2], \dots, [c n - 1, c n]$ . По предположению индукции существует $c$ такой, что $(n - 1)$ -я производная $f'$ в точке $c$ равна нулю.

Обобщения на другие области

Теорема Ролля — это свойство дифференцируемых функций по действительным числам, которые представляют собой упорядоченное поле . По существу, он не обобщается на другие поля , но делает следующее следствие: если действительный полином факторизуется (имеет все свои корни) по действительным числам, то его производная тоже делает это. Это свойство поля можно назвать свойством Ролля . ^{[ нужна ссылка ]} Более общие поля не всегда имеют дифференцируемые функции, но всегда имеют полиномы, которые можно дифференцировать символически. Точно так же более общие поля могут не иметь порядка, но существует понятие корня многочлена, лежащего в поле.

Таким образом, теорема Ролля показывает, что действительные числа обладают свойством Ролля. Любое алгебраически замкнутое поле, например комплексные числа, обладает свойством Ролля. Однако рациональные числа этого не делают – например, $x 3 - x = x (x - 1)(x + 1)$ факторизуется по рациональным числам , но его производная, $3x^{2}-1=3\left(x-{\tfrac {1}{\sqrt {3}}}\right)\left(x+{\tfrac {1}{\sqrt {3}}}\right),$ нет. Вопрос о том, какие поля удовлетворяют собственности Ролля, был поднят Каплански в 1972 году . ^{[ 4 ]} Для конечных полей ответ заключается в том, что только $F 2$ и $Ф 4$ иметь собственность Ролле. ^{[ 5 ]}^{[ 6 ]}

Сложную версию см. в индексе Вурхува .

См. также

Ссылки

^ Бесеньей А. (17 сентября 2012 г.). «Краткая история теоремы о среднем значении» (PDF) .
^ См. Каджори, Флориан (1999). История математики . Американское математическое соц. п. 224. ИСБН 9780821821022 .
^ Артин, Эмиль (1964) [1931], Гамма-функция , перевод Батлера, Майкла, Холта, Райнхарта и Уинстона , стр. 3–4 .
^ Каплански, Ирвинг (1972), Поля и кольца . ^{[ нужна полная цитата ]}
^ Крэйвен, Томас; Чордас, Джордж (1977), «Последовательности множителей для полей» , Illinois J. Math. , 21 (4): 801–817, doi : 10.1215/ijm/1256048929 .
^ Баллантайн, К.; Робертс, Дж. (январь 2002 г.), «Простое доказательство теоремы Ролля для конечных полей», The American Mathematical Monthly , 109 (1), Mathematical Association of America: 72–74, doi : 10.2307/2695770 , JSTOR 2695770 .

Дальнейшее чтение

Лейтольд, Луи (1972). Исчисление с аналитической геометрией (2-е изд.). Нью-Йорк: Харпер и Роу. стр. 201–207. ISBN 0-06-043959-9 .
Тейлор, Ангус Э. (1955). Продвинутое исчисление . Бостон: Джинн и компания. стр. 30–37.

Внешние ссылки

«Теорема Ролля» , Математическая энциклопедия , EMS Press , 2001 [1994]
Ролля и среднего Теоремы значения .
системы Mizar Доказательство : http://mizar.org/version/current/html/rolle.html#T2

[1] Бесеньей А. (17 сентября 2012 г.). «Краткая история теоремы о среднем значении» (PDF) .

[2] См. Каджори, Флориан (1999). История математики . Американское математическое соц. п. 224. ИСБН 9780821821022 .

[3] Артин, Эмиль (1964) [1931], Гамма-функция , перевод Батлера, Майкла, Холта, Райнхарта и Уинстона , стр. 3–4 .

[4] Каплански, Ирвинг (1972), Поля и кольца . ^{[ нужна полная цитата ]}

[5] Крэйвен, Томас; Чордас, Джордж (1977), «Последовательности множителей для полей» , Illinois J. Math. , 21 (4): 801–817, doi : 10.1215/ijm/1256048929 .

[6] Баллантайн, К.; Робертс, Дж. (январь 2002 г.), «Простое доказательство теоремы Ролля для конечных полей», The American Mathematical Monthly , 109 (1), Mathematical Association of America: 72–74, doi : 10.2307/2695770 , JSTOR 2695770 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]