Производная

Чтобы узнать о других значениях, см. Производная (значения) .

Производная , — это фундаментальный инструмент исчисления который количественно определяет чувствительность изменения выходного сигнала функции по отношению к ее входному значению. Производная функции одной переменной при выбранном входном значении, если она существует, представляет собой наклон к графику касательной функции в этой точке. Касательная линия является лучшим линейным приближением функции вблизи этого входного значения. По этой причине производную часто называют мгновенной скоростью изменения , отношением мгновенного изменения зависимой переменной к скорости изменения независимой переменной. Процесс нахождения производной называется дифференцированием .

Существует несколько различных обозначений дифференцирования, два из которых наиболее часто используются — это обозначение Лейбница и обозначение простых чисел. Обозначение Лейбница, названное в честь Готфрида Вильгельма Лейбница , представляется как отношение двух дифференциалов , тогда как обозначение простых чисел записывается путем добавления штрихового знака . Обозначения более высокого порядка представляют собой повторяющееся дифференцирование, и они обычно обозначаются в обозначениях Лейбница добавлением верхних индексов к дифференциалам, а в обозначениях простых чисел - добавлением дополнительных простых меток. Производные более высокого порядка могут применяться в физике; например, в то время как первая производная положения движущегося объекта по времени объекта — это скорость объекта , то, как положение меняется с течением времени, вторая производная — это ускорение , то, как скорость меняется с течением времени.

Производные можно обобщить на функции нескольких действительных переменных . В этом обобщении производная интерпретируется как линейное преобразование , график которого (после соответствующего перевода) является лучшим линейным приближением к графику исходной функции. Матрица Якобиана — это матрица , которая представляет это линейное преобразование относительно базиса, заданного выбором независимых и зависимых переменных. Его можно рассчитать через частные производные по независимым переменным. Для вещественной функции нескольких переменных матрица Якобиана сводится к вектору градиента .

Определение

В качестве ограничения

Функция действительной переменной $f(x)$ дифференцируема в точке $a$ своего домена , если его домен содержит открытый интервал , содержащий $a$, и предел

$$L=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$$

существует. Это означает, что для каждого положительного действительного числа $\varepsilon$, существует положительное действительное число $\delta$ такой, что для каждого $h$ такой, что $|h|<\delta$ и $h\neq 0$ затем $f(a+h)$ определяется, и

$$\left|L-{\frac {f(a+h)-f(a)}{h}}\right|<\varepsilon ,$$

где вертикальные полосы обозначают абсолютное значение . Это пример (ε, δ)-определения предела .

Если функция $f$ дифференцируема в $a$, то есть если предел $L$ называется производной существует, то этот предел $f$ в $a$. Существует несколько обозначений производной. Производная от $f$ в $a$ можно обозначить $f'(a)$, читай как " $f$ расцвет $a$"; или это можно обозначить ${\textstyle {\frac {df}{dx}}(a)}$читай как «производная от $f$ относительно $x$ в $a$" или " $df$ через (или более) $dx$ в $a$". См. § Обозначения ниже. Если $f$ — это функция, которая имеет производную в каждой точке своей области определения , то функцию можно определить, отобразив каждую точку $x$ к значению производной $f$ в $x$. Эта функция написана $f'$ и называется производной функцией или производной $f$. Функция $f$иногда имеет производную в большинстве, но не во всех точках своей области определения. Функция, значение которой в $a$ равно $f'(a)$ в любое время $f'(a)$ определено, а в других местах не определено, также называется производной от $f$. Это все еще функция, но ее область определения может быть меньше области определения $f$.

Например, пусть $f$ быть функцией возведения в квадрат: $f(x)=x^{2}$. Тогда частное в определении производной равно

$${\frac {f(a+h)-f(a)}{h}}={\frac {(a+h)^{2}-a^{2}}{h}}={\frac {a^{2}+2ah+h^{2}-a^{2}}{h}}=2a+h.$$

Деление на последнем шаге справедливо до тех пор, пока $h\neq 0$. Чем ближе $h$ это $0$, тем ближе это выражение становится к значению $2a$. Предел существует, и для каждого входа $a$ предел $2a$. Итак, производная функции возведения в квадрат – это функция удвоения: $f'(x)=2x$.

График функции , нарисованный черным цветом, и касательная линия к этому графику, нарисованная красным. Наклон . касательной равен производной функции в отмеченной точке

Производная в разных точках дифференцируемой функции. В этом случае производная равна $\sin \left(x^{2}\right)+2x^{2}\cos \left(x^{2}\right)$

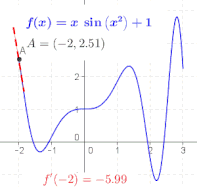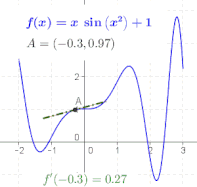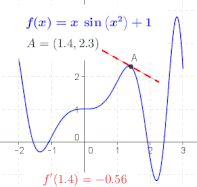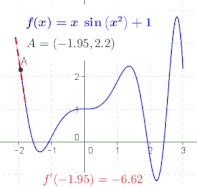
Отношение в определении производной – это наклон линии, проходящей через две точки на графике функции $f$, в частности точки $(a,f(a))$ и $(a+h,f(a+h))$. Как $h$ уменьшается, эти точки сближаются, а наклон этой линии приближается к предельному значению, наклон касательной к графику $f$ в $a$. Другими словами, производная — это наклон касательной.

Использование бесконечно малых

Один из способов думать о производной ${\textstyle {\frac {df}{dx}}(a)}$ представляет собой отношение бесконечно малого изменения выходного сигнала функции $f$ к бесконечно малому изменению входных данных. Чтобы сделать эту интуицию строгой, необходима система правил для манипулирования бесконечно малыми величинами. Система гипердействительных чисел — это способ рассмотрения бесконечных и бесконечно малых величин. Гиперреалистические числа являются расширением действительных чисел , которые содержат числа, большие, чем любые числа вида $1+1+\cdots +1$для любого конечного числа членов. Такие числа бесконечны, а их обратные величины бесконечно малы. Применение гипердействительных чисел к основам исчисления называется нестандартным анализом . Это дает возможность определить основные понятия исчисления, такие как производная и интеграл, в терминах бесконечно малых, тем самым придавая точное значение $d$в обозначениях Лейбница. Таким образом, производная от $f(x)$ становится

$$f'(x)=\operatorname {st} \left({\frac {f(x+dx)-f(x)}{dx}}\right)$$

для произвольного бесконечно малого $dx$, где $\operatorname {st}$ обозначает стандартную функцию части , которая «округляет» каждую конечную гиперреальную величину до ближайшей реальной. Взяв функцию возведения в квадрат $f(x)=x^{2}$ в качестве примера еще раз,

$${\begin{aligned}f'(x)&=\operatorname {st} \left({\frac {x^{2}+2x\cdot dx+(dx)^{2}-x^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx+(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left({\frac {2x\cdot dx}{dx}}+{\frac {(dx)^{2}}{dx}}\right)\\&=\operatorname {st} \left(2x+dx\right)\\&=2x.\end{aligned}}$$

Непрерывность и дифференцируемость

Эта функция не имеет производной в отмеченной точке, так как там функция не является непрерывной (в частности, имеет скачок разрыва ).

Функция абсолютного значения является непрерывной, но не может быть дифференцируемой при x = 0, поскольку наклоны касательных не приближаются к одному и тому же значению слева, как справа.

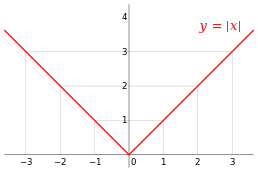
Если $f$ дифференцируема ​ в $a$, затем $f$ также должно быть непрерывным при $a$. В качестве примера выберите точку $a$ и разреши $f$ быть ступенчатой ​​функцией , которая возвращает значение 1 для всех $x$ меньше, чем $a$и возвращает разное значение 10 для всех $x$ больше или равно $a$. Функция $f$ не может иметь производную $a$. Если $h$ отрицательно, то $a+h$ находится в нижней части ступени, поэтому секущая линия от $a$ к $a+h$очень крутой; как $h$стремится к нулю, наклон стремится к бесконечности. Если $h$ положительно, то $a+h$ находится в верхней части ступени, поэтому секущая линия от $a$ к $a+h$имеет нулевой наклон. Следовательно, секущие линии не приближаются ни к одному наклону, поэтому предела разностного коэффициента не существует. Однако, даже если функция непрерывна в какой-то точке, она может быть там не дифференцируемой. Например, функция абсолютного значения , определяемая формулой $f(x)=|x|$ является непрерывным в $x=0$, но там оно не дифференцируемо. Если $h$ положительно, то наклон секущей от 0 до $h$это один; если $h$ отрицательно, то наклон секущей от $0$ к $h$ является $-1$. Графически это можно увидеть как «перегиб» или «перегиб» на графике. $x=0$. Даже функция с гладким графиком не является дифференцируемой в точке, где ее касательная вертикальна : например, функция, заданная формулой $f(x)=x^{1/3}$ не дифференцируема при $x=0$. Таким образом, функция, имеющая производную, является непрерывной, но существуют непрерывные функции, не имеющие производной.

Большинство функций, встречающихся на практике, имеют производные во всех или почти в каждой точке. На заре истории исчисления многие математики предполагали, что непрерывная функция дифференцируема в большинстве точек. В мягких условиях (например, если функция является монотонной или функцией Липшица ) это верно. Однако в 1872 году Вейерштрасс нашел первый пример функции, непрерывной всюду, но нигде не дифференцируемой. Этот пример теперь известен как функция Вейерштрасса . В 1931 году Стефан Банах доказал, что множество функций, имеющих производную в некоторой точке, является скудным множеством в пространстве всех непрерывных функций. Неформально это означает, что вряд ли какая-либо случайная непрерывная функция имеет производную хотя бы в одной точке.

Обозначения

Основная статья: Обозначения для дифференцирования

Одним из распространенных символов производной функции является обозначение Лейбница . Они записываются как частное двух дифференциалов $dy$ и $dx$, которые были введены Готфридом Вильгельмом Лейбницем в 1675 году. Оно до сих пор широко используется, когда уравнение $y=f(x)$рассматривается как функциональная связь между зависимыми и независимыми переменными . Первую производную обозначим через ${\textstyle {\frac {dy}{dx}}}$читай как «производная от $y$ относительно $x$". Эту производную можно альтернативно рассматривать как применение дифференциального оператора к функции: ${\textstyle {\frac {dy}{dx}}={\frac {d}{dx}}f(x).}$ Высшие производные выражаются с помощью обозначений ${\textstyle {\frac {d^{n}y}{dx^{n}}}}$ для $n$-я производная от $y=f(x)$. Это сокращения для многократного применения оператора производной; например, ${\textstyle {\frac {d^{2}y}{dx^{2}}}={\frac {d}{dx}}{\Bigl (}{\frac {d}{dx}}f(x){\Bigr )}.}$В отличие от некоторых альтернатив, нотация Лейбница предполагает явное указание переменной для дифференцирования в знаменателе, что устраняет неоднозначность при работе с несколькими взаимосвязанными величинами. Производную составной функции можно выразить с помощью правила цепочки : если $u=g(x)$ и $y=f(g(x))$ затем ${\textstyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}.}$

Другое распространенное обозначение дифференцирования — использование штриха в символе функции. $f(x)$. Это известно как простое обозначение , благодаря Жозефу-Луи Лагранжу . Первая производная записывается как $f'(x)$, читай как " $f$ расцвет $x$", или $y'$, читай как " $y$ основной". Аналогично вторую и третью производные можно записать как $f''$ и $f'''$, соответственно. Для обозначения количества высших производных за пределами этой точки некоторые авторы используют римские цифры в верхнем индексе , тогда как другие помещают число в круглые скобки, например: $f^{\mathrm {iv} }$ или $f^{(4)}.$ Последнее обозначение обобщается и дает обозначение $f^{(n)}$ для $n$-я производная от $f$.

В обозначениях Ньютона или точечной записи точка ставится над символом, обозначающим производную по времени. Если $y$ является функцией $t$, то первую и вторую производные можно записать как ${\dot {y}}$ и ${\ddot {y}}$, соответственно. Это обозначение используется исключительно для производных по времени или длине дуги . Обычно он используется в уравнениях физики дифференциальных и дифференциальной геометрии . Однако точечная запись становится неуправляемой для производных высокого порядка (порядка 4 и более) и не может работать с несколькими независимыми переменными.

Другое обозначение — D-нотация , которая представляет дифференциальный оператор символом $D.$ Первая производная записывается $Df(x)$ и высшие производные записываются с верхним индексом, поэтому $n$-я производная $D^{n}f(x).$ Это обозначение иногда называют обозначением Эйлера , хотя кажется, что Леонард Эйлер его не использовал, а обозначение было введено Луи Франсуа Антуаном Арбогастом . Чтобы указать частную производную, переменная, дифференцируемая по которой, обозначается индексом, например, для функции $u=f(x,y),$ его частная производная по $x$ можно написать $D_{x}u$ или $D_{x}f(x,y).$ Высшие частные производные могут обозначаться верхними индексами или несколькими индексами, например ${\textstyle D_{xy}f(x,y)={\frac {\partial }{\partial y}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$ и ${\textstyle D_{x}^{2}f(x,y)={\frac {\partial }{\partial x}}{\Bigl (}{\frac {\partial }{\partial x}}f(x,y){\Bigr )}}$.

Правила вычислений

Основная статья: Правила дифференциации

В принципе, производную функции можно вычислить на основе определения, рассмотрев разностный коэффициент и вычислив его предел. Если известны производные нескольких простых функций, производные других функций легче вычислить, используя правила получения производных более сложных функций из более простых. Этот процесс нахождения производной известен как дифференцирование .

Правила для основных функций

Ниже приведены правила для производных наиболее распространенных основных функций. Здесь, $a$ является действительным числом, и $e$ — математическая константа, равная приблизительно 2,71828 .

• Производные степени :

  ${\frac {d}{dx}}x^{a}=ax^{a-1}$

• Функции экспоненты , натурального логарифма и логарифма с общим основанием :

  ${\frac {d}{dx}}e^{x}=e^{x}$

  ${\frac {d}{dx}}a^{x}=a^{x}\ln(a)$, для $a>0$

  ${\frac {d}{dx}}\ln(x)={\frac {1}{x}}$, для $x>0$

  ${\frac {d}{dx}}\log _{a}(x)={\frac {1}{x\ln(a)}}$, для $x,a>0$

• Тригонометрические функции :

  ${\frac {d}{dx}}\sin(x)=\cos(x)$

  ${\frac {d}{dx}}\cos(x)=-\sin(x)$

  ${\frac {d}{dx}}\tan(x)=\sec ^{2}(x)={\frac {1}{\cos ^{2}(x)}}=1+\tan ^{2}(x)$

• Обратные тригонометрические функции :

  ${\frac {d}{dx}}\arcsin(x)={\frac {1}{\sqrt {1-x^{2}}}}$, для $-1<x<1$

  ${\frac {d}{dx}}\arccos(x)=-{\frac {1}{\sqrt {1-x^{2}}}}$, для $-1<x<1$

  ${\frac {d}{dx}}\arctan(x)={\frac {1}{1+x^{2}}}$

Правила для совмещенных функций

Учитывая, что $f$ и $g$это функции. Ниже приведены некоторые из самых основных правил вывода производной функции из производных основных функций.

• Постоянное правило : если $f$ постоянна, то для всех $x$,

  $f'(x)=0.$

• Правило суммы :

  $(\alpha f+\beta g)'=\alpha f'+\beta g'$ для всех функций $f$ и $g$ и все действительные числа $\alpha$ и $\beta$.

• Правило продукта :

  $(fg)'=f'g+fg'$ для всех функций $f$ и $g$. В качестве частного случая это правило включает в себя тот факт, что $(\alpha f)'=\alpha f'$ в любое время $\alpha$ является константой, потому что $\alpha 'f=0\cdot f=0$ по постоянному правилу.

• Правило частностей :

  $\left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}$ для всех функций $f$ и $g$ на всех входах, где g ≠ 0 .

• Цепное правило для составных функций : Если $f(x)=h(g(x))$, затем

  $f'(x)=h'(g(x))\cdot g'(x).$

Пример расчета

Производная функции, заданной выражением $f(x)=x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7$ является

$${\begin{aligned}f'(x)&=4x^{(4-1)}+{\frac {d\left(x^{2}\right)}{dx}}\cos \left(x^{2}\right)-{\frac {d\left(\ln {x}\right)}{dx}}e^{x}-\ln(x){\frac {d\left(e^{x}\right)}{dx}}+0\\&=4x^{3}+2x\cos \left(x^{2}\right)-{\frac {1}{x}}e^{x}-\ln(x)e^{x}.\end{aligned}}$$

Здесь второй член вычислялся с использованием правила цепочки , а третий член — с помощью правила произведения . Известные производные элементарных функций $x^{2}$, $x^{4}$, $\sin(x)$, $\ln(x)$, и $\exp(x)=e^{x}$, а также постоянная $7$, также использовались.

Производные высшего порядка

Производные более высокого порядка означают, что функция дифференцируется неоднократно. При условии $f$ дифференцируемая функция, производная $f$ – первая производная, обозначаемая как $f'$. Производная от $f'$ — вторая производная , обозначаемая как $f''$и производная от $f''$ — третья производная , обозначаемая как $f'''$. Продолжая этот процесс, если он существует, $n$-th производная как производная $(n-1)$- ая производная или производная порядка $n$. Как уже говорилось выше , обобщение производной функции $f$ может быть обозначен как $f^{(n)}$. Функция, имеющая $k$ последовательные производные называются $k$раз дифференцируемы . Если $k$- производная непрерывна, то говорят, что функция принадлежит классу дифференцируемости $C^{k}$. Функция, имеющая бесконечное число производных, называется бесконечно дифференцируемой или гладкой . Одним из примеров бесконечно дифференцируемой функции является полиномиальная ; дифференцирование этой функции многократно приводит к постоянной функции , а все бесконечно последующие производные этой функции равны нулю.

В одном из приложений производные более высокого порядка могут иметь специфическую интерпретацию в физике . Предположим, что функция представляет положение объекта в данный момент. Первая производная этой функции — это скорость объекта по времени, вторая производная функции — это ускорение объекта по времени. и третья производная – это рывок .

В других измерениях

См. Также: Векторное исчисление и многомерное исчисление.

Векторные функции

Векторнозначная функция $\mathbf {y}$ действительной переменной отправляет действительные числа в векторы в некотором векторном пространстве $\mathbb {R} ^{n}$. Вектор-функцию можно разбить на ее координатные функции. $y_{1}(t),y_{2}(t),\dots ,y_{n}(t)$, означающий, что $\mathbf {y} =(y_{1}(t),y_{2}(t),\dots ,y_{n}(t))$. Сюда входят, например, параметрические кривые в $\mathbb {R} ^{2}$ или $\mathbb {R} ^{3}$. Координатные функции являются вещественными функциями, поэтому к ним применимо приведенное выше определение производной. Производная от $\mathbf {y} (t)$определяется как вектор , называемый касательным вектором , координаты которого являются производными координатных функций. То есть,

$$\mathbf {y} '(t)=\lim _{h\to 0}{\frac {\mathbf {y} (t+h)-\mathbf {y} (t)}{h}},$$

если предел существует. Вычитание в числителе — это вычитание векторов, а не скаляров. Если производная от $\mathbf {y}$ существует для любого значения $t$, затем $\mathbf {y}$ — еще одна векторная функция.

Частные производные

Основная статья: Частная производная

Функции могут зависеть от более чем одной переменной . Частная производная функции нескольких переменных — это ее производная по одной из этих переменных, при этом остальные остаются постоянными. Частные производные используются в векторном исчислении и дифференциальной геометрии . Как и в случае с обычными производными, существует несколько обозначений: частная производная функции $f(x,y,\dots )$ относительно переменной $x$ по-разному обозначается

$f_{x}$, $f'_{x}$, $\partial _{x}f$, ${\frac {\partial }{\partial x}}f$, или ${\frac {\partial f}{\partial x}}$,

среди других возможностей. Его можно рассматривать как скорость изменения функции в $x$-направление. Здесь ∂ — это округленная цифра d , называемая символом частной производной . Чтобы отличить его от буквы d , ∂ иногда произносится как «der», «del» или «partial» вместо «dee». Например, пусть $f(x,y)=x^{2}+xy+y^{2}$, то частная производная функции $f$ по обеим переменным $x$ и $y$ соответственно:

$${\frac {\partial f}{\partial x}}=2x+y,\qquad {\frac {\partial f}{\partial y}}=x+2y.$$

В общем случае частная производная функции $f(x_{1},\dots ,x_{n})$ в направлении $x_{i}$ в точку $(a_{1},\dots ,a_{n})$ определяется как:

$${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{i},\ldots ,a_{n})}{h}}.$$

Это имеет основополагающее значение для изучения функций нескольких действительных переменных . Позволять $f(x_{1},\dots ,x_{n})$быть такой вещественной функцией . Если все частные производные $f$ относительно $x_{j}$ определены в точке $(a_{1},\dots ,a_{n})$, эти частные производные определяют вектор

$$\nabla f(a_{1},\ldots ,a_{n})=\left({\frac {\partial f}{\partial x_{1}}}(a_{1},\ldots ,a_{n}),\ldots ,{\frac {\partial f}{\partial x_{n}}}(a_{1},\ldots ,a_{n})\right),$$

называется градиентом который $f$ в $a$. Если $f$ дифференцируема в каждой точке некоторой области, то градиент является вектор-функцией $\nabla f$ это отображает точку $(a_{1},\dots ,a_{n})$ к вектору $\nabla f(a_{1},\dots ,a_{n})$. Следовательно, градиент определяет векторное поле .

Производные по направлению

Основная статья: Производная по направлению

Если $f$ является вещественной функцией на $\mathbb {R} ^{n}$, то частные производные $f$измерить ее изменение в направлении осей координат. Например, если $f$ является функцией $x$ и $y$, то его частные производные измеряют изменение $f$ в $x$ и $y$направление. Однако они не измеряют напрямую изменение $f$ в любом другом направлении, например, вдоль диагональной линии $y=x$. Они измеряются с использованием производных по направлению. Выберите вектор $\mathbf {v} =(v_{1},\ldots ,v_{n})$, то по направлению производная $f$ в направлении $\mathbf {v}$ в точку $\mathbf {x}$ является:

$$D_{\mathbf {v} }{f}(\mathbf {x} )=\lim _{h\rightarrow 0}{\frac {f(\mathbf {x} +h\mathbf {v} )-f(\mathbf {x} )}{h}}.$$

Если все частные производные $f$ существуют и непрерывны в $\mathbf {x}$, то определяют производную по направлению $f$ в направлении $\mathbf {v}$ по формуле:

$$D_{\mathbf {v} }{f}(\mathbf {x} )=\sum _{j=1}^{n}v_{j}{\frac {\partial f}{\partial x_{j}}}.$$

Полная производная, полный дифференциал и матрица Якобиана

Основная статья: Полная производная

Когда $f$ является функцией из открытого подмножества $\mathbb {R} ^{n}$ к $\mathbb {R} ^{m}$, то производная по направлению $f$ в выбранном направлении является лучшим линейным приближением к $f$в тот момент и в этом направлении. Однако, когда $n>1$, ни одна производная по направлению не может дать полную картину поведения $f$. Полная производная дает полную картину, рассматривая все направления одновременно. То есть для любого вектора $\mathbf {v}$ начинается с $\mathbf {a}$, справедлива формула линейной аппроксимации:

$$f(\mathbf {a} +\mathbf {v} )\approx f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {v} .$$

Аналогично с производной с одной переменной: $f'(\mathbf {a} )$выбирается так, чтобы ошибка в этом приближении была как можно меньше. Полная производная от $f$ в $\mathbf {a}$ — единственное линейное преобразование $f'(\mathbf {a} )\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}$ такой, что

$$\lim _{\mathbf {h} \to 0}{\frac {\lVert f(\mathbf {a} +\mathbf {h} )-(f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {h} )\rVert }{\lVert \mathbf {h} \rVert }}=0.$$

Здесь $\mathbf {h}$ является вектором в $\mathbb {R} ^{n}$, поэтому норма в знаменателе — это стандартная длина на $\mathbb {R} ^{n}$. Однако, $f'(\mathbf {a} )\mathbf {h}$ является вектором в $\mathbb {R} ^{m}$, а норма в числителе — это стандартная длина на $\mathbb {R} ^{m}$. Если $v$ вектор, начинающийся с $a$, затем $f'(\mathbf {a} )\mathbf {v}$ называется вперед продвижением $\mathbf {v}$ к $f$.

Если полная производная существует при $\mathbf {a}$, то все частные производные и производные по направлению $f$ существовать в $\mathbf {a}$, и для всех $\mathbf {v}$, $f'(\mathbf {a} )\mathbf {v}$ является производной по направлению $f$ в направлении $\mathbf {v}$. Если $f$ записывается с использованием координатных функций, так что $f=(f_{1},f_{2},\dots ,f_{m})$, то полную производную можно выразить с помощью частных производных в виде матрицы . Эта матрица называется Якобиана матрицей $f$ в $\mathbf {a}$:

$$f'(\mathbf {a} )=\operatorname {Jac} _{\mathbf {a} }=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{ij}.$$

Обобщения

Основная статья: Обобщения производной

Понятие дериватива можно распространить на многие другие ситуации. Общей нитью является то, что производная функции в точке служит линейным приближением функции в этой точке.

• Важное обобщение производной касается комплексных функций комплексных переменных , таких как функции из (области) комплексных чисел. $\mathbb {C}$ к $\mathbb {C}$. Понятие производной такой функции получается заменой в определении вещественных переменных комплексными. Если $\mathbb {C}$ отождествляется с $\mathbb {R} ^{2}$ написав комплексное число $z$ как $x+iy$, то дифференцируемая функция из $\mathbb {C}$ к $\mathbb {C}$ заведомо дифференцируема как функция от $\mathbb {R} ^{2}$ к $\mathbb {R} ^{2}$ (в том смысле, что все его частные производные существуют), но обратное в целом неверно: комплексная производная существует только в том случае, если действительная производная является комплексной линейной , и это накладывает отношения между частными производными, называемые уравнениями Коши – Римана - см. голоморфные функции .
• Другое обобщение касается функций между дифференцируемыми или гладкими многообразиями . Интуитивно говоря, такое многообразие $M$ это пространство, которое можно аппроксимировать вблизи каждой точки $x$ векторным пространством, называемым его касательным пространством : прототипным примером является гладкая поверхность в $\mathbb {R} ^{3}$. Производная (или дифференциал) (дифференцируемого) отображения $f:M\to N$ между многообразиями, в точке $x$ в $M$, тогда является линейным отображением касательного пространства $M$ в $x$ к касательному пространству $N$ в $f(x)$. Производная функция становится отображением между касательными расслоениями $M$ и $N$. Это определение используется в дифференциальной геометрии .
• Дифференциация также может быть определена для карт векторного пространства , такого как банахово пространство , в котором этими обобщениями являются производная Гато и производная Фреше .
• Одним из недостатков классической производной является то, что очень многие функции не дифференцируемы. Тем не менее, существует способ расширить понятие производной, чтобы все непрерывные функции и многие другие функции можно было дифференцировать, используя концепцию, известную как слабая производная . Идея состоит в том, чтобы встроить непрерывные функции в большее пространство, называемое пространством распределений , и потребовать, чтобы функция была дифференцируемой только «в среднем».
• Свойства производной вдохновили на введение и изучение многих подобных объектов в алгебре и топологии; примером является дифференциальная алгебра . Здесь он состоит из вывода некоторых тем абстрактной алгебры, таких как кольца , идеалы , поля и так далее.
• Дискретным эквивалентом дифференцирования являются конечные разности . Изучение дифференциального исчисления объединено с исчислением конечных разностей в исчислении шкалы времени .
• Арифметическая производная включает в себя функцию, которая определяется для целых чисел путем простой факторизации . Это аналогия с правилом продукта.

Смотрите также

• интеграл

Рекомендации

• Апостол, Том М. (июнь 1967 г.), Calculus, Vol. 1: Исчисление с одной переменной и введение в линейную алгебру , том. 1 (2-е изд.), Уайли, ISBN  978-0-471-00005-1
• Азегами, Хидеюки (2020), Проблемы оптимизации формы , Оптимизация Springer и ее приложения, том. 164, Спрингер, номер домена : 10.1007/978-981-15-7618-8 , ISBN.  978-981-15-7618-8 , S2CID   226442409
• Банах, Стефан (1931), «О категории Бэра некоторых наборов функций» , Studia Math. , 3 (3): 174–179, doi : 10.4064/sm-3-1-174-179 .
• Барбо, Э.Дж. (1961). «Замечания об арифметической производной» . Канадский математический бюллетень . 4 (2): 117–122. дои : 10.4153/CMB-1961-013-0 . Збл   0101.03702 .
• Бхардвадж, Р.С. (2005), Математика для экономики и бизнеса (2-е изд.), Excel Books India, ISBN  9788174464507
• Каджори, Флориан (1923), «История обозначений исчисления», Annals of Mathematics , 25 (1): 1–46, doi : 10.2307/1967725 , hdl : 2027/mdp.39015017345896 , JSTOR   1967725
• Каджори, Флориан (2007), История математических обозначений , том. 2, Классика Козимо, ISBN  978-1-60206-713-4
• Карозерс, Нидерланды (2000), Реальный анализ , Издательство Кембриджского университета
• Чоудари, АДР; Никулеску, Константин П. (2014), Реальный анализ интервалов , Springer India, doi : 10.1007/978-81-322-2148-7 , ISBN  978-81-322-2148-7
• Кристофер, Эссекс (2013), Исчисление: полный курс , Пирсон, с. 682, ISBN  9780321781079 , OCLC   872345701
• Курант, Ричард ; Джон, Фриц (22 декабря 1998 г.), Введение в исчисление и анализ, Vol. 1 , Springer-Verlag , doi : 10.1007/978-1-4613-8955-2 , ISBN  978-3-540-65058-4
• Дэвид, Клэр (2018), «Обход динамических систем: простой способ получить размерность графика функции Вейерштрасса», Труды Международного центра геометрии , 11 (2), Академия наук Украины: 53 –68, arXiv : 1711.10349 , doi : 10.15673/tmgc.v11i2.1028
• Давваз, Бижан (2023), Векторы и функции нескольких переменных , Springer, doi : 10.1007/978-981-99-2935-1 , ISBN  978-981-99-2935-1 , S2CID   259885793
• Дебнат, Локенат; Шах, Фирдоус Ахмад (2015), Вейвлет-преобразования и их приложения (2-е изд.), Birkhäuser, doi : 10.1007/978-0-8176-8418-1 , ISBN  978-0-8176-8418-1
• Эванс, Лоуренс (1999), Уравнения в частных производных , Американское математическое общество, ISBN  0-8218-0772-2
• Ивс, Ховард (2 января 1990 г.), Введение в историю математики (6-е изд.), Брукс Коул, ISBN  978-0-03-029558-4
• Фунаро, Даниэле (1992), Полиномиальная аппроксимация дифференциальных уравнений , Конспекты лекций в монографиях по физике, том. 8, Спрингер, номер домена : 10.1007/978-3-540-46783-0 , ISBN.  978-3-540-46783-0
• Гбур, Грег (2011), Математические методы оптической физики и техники , Издательство Кембриджского университета, Бибкод : 2011mmop.book.....G , ISBN  978-1-139-49269-0
• Георгиев, Светлин Г. (2018), Дробное динамическое исчисление и дробные динамические уравнения на временных масштабах , Springer, doi : 10.1007/978-3-319-73954-0 , ISBN  978-3-319-73954-0
• Гудман, AW (1963), Аналитическая геометрия и исчисление , The MacMillan Company
• Гоник, Ларри (2012), Мультяшное руководство по исчислению , Уильям Морроу, ISBN  978-0-06-168909-3
• Грей, Альфред; Аббена, Эльза; Саламон, Саймон (2006), Современная дифференциальная геометрия кривых и поверхностей с помощью Mathematica , CRC Press, ISBN  978-1-58488-448-4
• Гузман, Альберто (2003), Производные и интегралы функций многих переменных , Springer, doi : 10.1007/978-1-4612-0035-2 , ISBN  978-1-4612-0035-2
• Хенле, Джеймс М.; Кляйнберг, Юджин М. (2003), Исчисление бесконечно малых , Dover Publications, ISBN  978-0-486-42886-4
• Хьюитт, Эдвин ; Стромберг, Карл Р. (1965), Реальный и абстрактный анализ , Springer-Verlag, Теорема 17.8, doi : 10.1007/978-3-662-29794-0 , ISBN  978-3-662-28275-5
• Яшек, Мартин (1922), «Функция Бользановой» (PDF) , Журнал по развитию математики и физики (на чешском языке), 51 (2): 69–76, doi : 10.21136/CPMF.1922.121916
• Ярник, Войтех (1922), «О функции Больцано» (PDF) , Журнал по развитию математики и физики (на чешском языке), 51 (4): 248–264, doi : 10.21136/CPMF.1922.109021 . Смотрите английскую версию здесь .
• Кейслер, Х. Джером (2012) [1986], Элементарное исчисление: подход с использованием бесконечно малых (2-е изд.), Приндл, Вебер и Шмидт, ISBN  978-0-871-50911-6
• Колчин, Эллис (1973), Дифференциальная алгебра и алгебраические группы , Academic Press, ISBN  978-0-08-087369-5
• Крейциг, Эрвин (1991), Дифференциальная геометрия , Нью-Йорк: Дувр , ISBN  0-486-66721-9
• Ларсон, Рон; Хостетлер, Роберт П.; Эдвардс, Брюс Х. (28 февраля 2006 г.), Исчисление: ранние трансцендентные функции (4-е изд.), Houghton Mifflin Company, ISBN  978-0-618-60624-5
• Ли, Джон М. (2013), Введение в гладкие многообразия , Тексты для аспирантов по математике, том. 218, Спрингер, номер домена : 10.1007/978-0-387-21752-9 , ISBN.  978-0-387-21752-9
• Матай, AM; Хаубольд, Х.Дж. (2017), Дробное исчисление и многомерное исчисление: проблемы построения и оптимизации моделей , Springer, doi : 10.1007/978-3-319-59993-9 , ISBN  978-3-319-59993-9
• Мур, Уилл Х.; Сигел, Дэвид А. (2013), Математический курс политических и социальных исследований , Princeton University Press, ISBN  978-0-691-15995-9
• Руссос, Иоаннис М. (2014), Неправильный интеграл Римана , CRC Press , ISBN  978-1-4665-8807-3
• Рыхлик, Карел (1923), О функции из рукописных документов Больцано.
• Шварцман, Стивен (1994), Слова математики: этимологический словарь математических терминов, используемых на английском языке , Американская математическая ассоциация, ISBN  9781614445012
• Сильверман, Ричард А. (1989), Основы исчисления: с приложениями , Courier Corporation, ISBN  9780486660974
• Стюарт, Джеймс (24 декабря 2002 г.), Исчисление (5-е изд.), Брукс Коул, ISBN  978-0-534-39339-7
• Стрэнг, Гилберт ; и другие. (2023), Исчисление, том 1 , OpenStax, ISBN  978-1-947172-13-5
• Томпсон, Сильванус П. (8 сентября 1998 г.), Calculus Made Easy (пересмотренное, обновленное, расширенное издание), Нью-Йорк: St. Martin's Press, ISBN  978-0-312-18548-0
• Варберг, Дейл Э.; Перселл, Эдвин Дж.; Ригдон, Стивен Э. (2007), Исчисление (9-е изд.), Пирсон Прентис Холл , ISBN  978-0131469686
• Уорнер, Фрэнк В. (1983), Основы дифференцируемых многообразий и групп Ли , Springer, ISBN  978-0-387-90894-6

Внешние ссылки

• «Производная» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Академия Хана : «Ньютон, Лейбниц и Усэйн Болт»
• Вайсштейн, Эрик В. «Производная» . Математический мир .
• Онлайн-калькулятор производных от Wolfram Alpha .