Теория представлений

Эта статья посвящена теории представлений алгебраических структур линейными преобразованиями и матрицами. Для теории представления в других дисциплинах см. Представление (значения) .

Не путать с групповой презентацией .

Теория представлений изучает, как алгебраические структуры «действуют» на объекты. Простой пример — как симметрии правильных многоугольников , состоящие из отражений и вращений, преобразуют многоугольник.

Теория представлений — это раздел математики , который изучает абстрактные алгебраические структуры их , представляя элементы в виде линейных преобразований векторных пространств , и изучает модули над этими абстрактными алгебраическими структурами. По сути, представление делает абстрактный алгебраический объект более конкретным, описывая его элементы матрицами и их алгебраическими операциями (например, сложение матриц , умножение матриц ). Теория матриц и линейных операторов хорошо изучена. поэтому представление более абстрактных объектов в терминах знакомых объектов линейной алгебры помогает выявить свойства, а иногда и упростить вычисления по более абстрактным теориям.

К алгебраическим объектам, поддающимся такому описанию, относятся группы , ассоциативные алгебры и алгебры Ли . Наиболее известной из них (и исторически первой) является теория представления групп , в которой элементы группы представлены обратимыми матрицами, так что групповая операция представляет собой умножение матриц.

Теория представлений — полезный метод, поскольку она сводит проблемы абстрактной алгебры к задачам линейной алгебры — предмета, который хорошо изучен. Например, представление группы бесконечномерным гильбертовым пространством позволяет применять методы анализа к теории групп. Более того, теория представлений важна в физике, поскольку она может описать, как группа симметрии физической системы влияет на решения уравнений, описывающих эту систему.

Теория представлений широко распространена во всех областях математики. Приложения теории представлений разнообразны. Помимо влияния на алгебру, теория представлений

• обобщает анализ Фурье посредством гармонического анализа ,
• связан с геометрией через теорию инвариантов и программу Эрлангена ,
• оказывает влияние на теорию чисел через автоморфные формы и программу Ленглендса .

Существуют различные подходы к теории представлений. Одни и те же объекты можно изучать методами алгебраической геометрии , теории модулей , аналитической теории чисел , дифференциальной геометрии , теории операторов , алгебраической комбинаторики и топологии .

Успех теории представлений привел к многочисленным обобщениям. Один из наиболее общих — в теории категорий . Алгебраические объекты, к которым применяется теория представлений, можно рассматривать как особые виды категорий, а представления — как функторы из категории объектов в категорию векторных пространств . Это описание указывает на два очевидных обобщения: во-первых, алгебраические объекты можно заменить более общими категориями; во-вторых, целевую категорию векторных пространств можно заменить другими хорошо понятными категориями.

Определения и понятия

Позволять $V$ быть векторным пространством над полем $\mathbb {F}$. Например, предположим $V$ является $\mathbb {R} ^{n}$ или $\mathbb {C} ^{n}$, стандартное n -мерное пространство векторов-столбцов над действительными или комплексными числами соответственно. В этом случае идея теории представлений состоит в том, чтобы конкретно заниматься абстрактной алгеброй, используя $n\times n$ матрицы действительных или комплексных чисел.

Есть три основных типа алгебраических объектов, для которых это можно сделать: группы , ассоциативные алгебры и алгебры Ли .

• Набор всех обратимых $n\times n$ Матрицы — это группа при умножении матриц , а теория представлений групп анализирует группу, описывая («представляя») ее элементы в терминах обратимых матриц.
• Сложение и умножение матриц составляют набор всех $n\times n$ матрицы в ассоциативную алгебру, и, следовательно, существует соответствующая теория представлений ассоциативных алгебр .
• Если заменить матричное умножение $MN$ матричным коммутатором $MN-NM$, тогда $n\times n$ вместо этого матрицы становятся алгеброй Ли, что приводит к теории представлений алгебр Ли .

Это распространяется на любую область $\mathbb {F}$ и любое векторное пространство $V$ над $\mathbb {F}$, где линейные карты заменяют матрицы, а композиция заменяет умножение матриц: существует группа ${\text{GL}}(V,\mathbb {F} )$ автоморфизмов ​ ​ $V$, ассоциативная алгебра ${\text{End}}_{\mathbb {F} }(V)$ всех эндоморфизмов $V$и соответствующая алгебра Ли ${\mathfrak {gl}}(V,\mathbb {F} )$.

Определение

См. также: представление группы , представление алгебры и представление алгебры Ли.

Действие

Существует два способа определения представления. Первый использует идею действия , обобщая способ воздействия матриц на вектор-столбцы путем умножения матриц.

Представительство ​ группы ​ $G$ или (ассоциативная или лиева) алгебра $A$ в векторном пространстве $V$ это карта

$$\Phi \colon G\times V\to V\quad {\text{or}}\quad \Phi \colon A\times V\to V$$

с двумя свойствами.

1. Для любого $g$ в $G$ (или $a$ в $A$), карта
   $${\begin{aligned}\Phi (g)\colon V&\to V\\v&\mapsto \Phi (g,v)\end{aligned}}$$
   линейна (по $\mathbb {F}$).
2. Если ввести обозначение g · v для $\Phi$ ( g , v ), тогда для любых g ₁ , g ₂ в G и v в V :
   $$(2.1)\quad e\cdot v=v$$
   $$(2.2)\quad g_{1}\cdot (g_{2}\cdot v)=(g_{1}g_{2})\cdot v$$
   где e — единичный элемент G , а g ₁ g ₂ — групповое произведение G. в

Определение ассоциативных алгебр аналогично, за исключением того, что ассоциативные алгебры не всегда имеют единицу, и в этом случае уравнение (2.1) опускается. Уравнение (2.2) представляет собой абстрактное выражение ассоциативности умножения матриц. Это не относится к матричному коммутатору, а также для коммутатора не существует единичного элемента. для алгебр Ли единственное требование состоит в том, чтобы для x1 _любых , x2 _{Следовательно ,} в A и v в V :

$$(2.2')\quad x_{1}\cdot (x_{2}\cdot v)-x_{2}\cdot (x_{1}\cdot v)=[x_{1},x_{2}]\cdot v$$

где [ x1 _, обобщающая x2 _, ] — скобка Ли матричный коммутатор MN − NM .

Картирование

Второй способ определения представления фокусируется на отображении φ , отправляющем g в G в линейное отображение φ ( g ): V → V , которое удовлетворяет условию

$\varphi (g_{1}g_{2})=\varphi (g_{1})\circ \varphi (g_{2})\quad {\text{for all }}g_{1},g_{2}\in G$

и аналогично в остальных случаях. Этот подход является одновременно более кратким и более абстрактным. С этой точки зрения:

• представлением группы G в векторном пространстве V является гомоморфизм группы φ : G → GL( V , F );
• представлением ассоциативной алгебры A в векторном пространстве V является гомоморфизм алгебры φ : A → End _F ( V );
• представление алгебры Ли ${\mathfrak {a}}$ в векторном пространстве $V$ является гомоморфизмом алгебры Ли $\phi :{\mathfrak {a}}\to {\mathfrak {gl}}(V,\mathbb {F} )$.

Терминология

Векторное пространство V называется представления пространством φ , а его размерность (если конечная) называется размерностью представления (иногда степенью , как в ). Также общепринято называть само V представлением, когда гомоморфизм φ ясен из контекста; в противном случае обозначение ( V , φ ) может использоваться для обозначения представления.

Когда V имеет конечную размерность n , можно выбрать основу для V , чтобы отождествить V с F. ^н и, следовательно, восстановить матричное представление с записями в поле F .

Эффективное или точное представление — это представление ( V , φ которого гомоморфизм φ инъективен ), для .

Эквивариантные

См. Также: Эквивариантная карта.

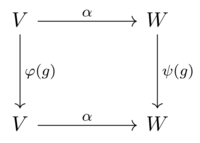
Если V и W — векторные пространства над F , снабженные представлениями φ и ψ группы G , то эквивариантное отображение из V в W — это линейное отображение α : V → W такое, что

$\alpha (g\cdot v)=g\cdot \alpha (v)$

для всех g в G и v в V . В терминах φ : G → GL( V ) и ψ : G → GL( W ) это означает

$\alpha \circ \varphi (g)=\psi (g)\circ \alpha$

для всех g в G следующая , то есть коммутирует диаграмма :

Аналогично определяются эквивариантные отображения представлений ассоциативной алгебры или алгебры Ли. Если α обратимо, то оно называется изоморфизмом , и в этом случае V и W (или, точнее, φ и ψ ) являются изоморфными представлениями , также называемыми эквивалентными представлениями . Эквивариантную карту часто называют картой переплетения представлений. Кроме того, в случае группы G ее иногда называют G -отображением.

Изоморфные представления для практических целей «одинаковы»; они предоставляют одну и ту же информацию о представляемой группе или алгебре. Поэтому теория представлений стремится классифицировать представления с точностью до изоморфизма .

, факторы и

См. Также: Неприводимое представление и простой модуль.

Если $(V,\psi )$ является представлением (скажем) группы $G$, и $W$ является линейным подпространством $V$ который сохраняется под действием $G$ в том смысле, что для всех $w\in W$ и $g\in G$, $g\cdot w\in W$ ( Серр называет это $W$ конюшня под $G$), затем $W$ называется подпредставлением : определяя

$$\phi :G\to {\text{Aut}}(W)$$

где $\phi (g)$ это ограничение $\psi (g)$ к $W$, $(W,\phi )$ является представлением $G$ и включение $W\hookrightarrow V$является эквивариантным отображением. Факторпространство ​ $V/W$ также может быть превращено в представление $G$. Если $V$ имеет ровно два подпредставления, а именно тривиальное подпространство {0} и $V$само по себе, то представление называется неприводимым ; если $V$ имеет собственное нетривиальное подпредставление, то представление называется приводимым .

Из определения неприводимого представления следует лемма Шура : эквивариантное отображение.

$$\alpha :(V,\psi )\to (V',\psi ')$$

между неприводимыми представлениями является либо нулевым отображением , либо изоморфизмом, поскольку его ядро ​​и образ являются подпредставлениями. В частности, когда $V=V'$ что эквивариантные эндоморфизмы , это показывает , $V$образуют ассоциативную алгебру с делением над основным полем F . Если F , алгебраически замкнуто единственными эквивариантными эндоморфизмами неприводимого представления являются скалярные кратные единицы.

Неприводимые представления являются строительными блоками теории представлений для многих групп: если представление $V$не является неприводимым, то оно построено из подпредставления и фактора, которые в некотором смысле «проще»; например, если $V$конечномерно, то и подпредставление, и фактор имеют меньшую размерность. Существуют контрпримеры, когда представление имеет подпредставление, но имеет только один нетривиальный неприводимый компонент. Например, аддитивная группа $(\mathbb {R} ,+)$ имеет двумерное представление

$$\phi (a)={\begin{bmatrix}1&a\\0&1\end{bmatrix}}$$

Эта группа имеет вектор ${\begin{bmatrix}1&0\end{bmatrix}}^{\mathsf {T}}$ фиксируется этим гомоморфизмом, но подпространство дополнения отображается в

$${\begin{bmatrix}0\\1\end{bmatrix}}\mapsto {\begin{bmatrix}a\\1\end{bmatrix}}$$

дающее только одно неприводимое подпредставление. Это справедливо для всех унипотентных групп .

Прямые суммы и неразложимые представления

См. также: Прямая сумма , неразложимый модуль и полупростой модуль.

Если ( V , φ ) и ( W , ψ ) являются представлениями (скажем) группы G , то прямая сумма V и W является представлением каноническим образом через уравнение

$g\cdot (v,w)=(g\cdot v,g\cdot w).$

Прямая сумма двух представлений несет в себе не больше информации о группе G , чем два представления по отдельности. Если представление является прямой суммой двух собственных нетривиальных подпредставлений, то оно называется разложимым. В противном случае говорят, что оно неразложимо.

Полная сводимость

При благоприятных обстоятельствах всякое конечномерное представление представляет собой прямую сумму неприводимых представлений: такие представления называются полупростыми . В этом случае достаточно понимать только неприводимые представления. Примеры явления « полной сводимости » включают конечные группы (см. теорему Машке ), компактные группы и полупростые алгебры Ли.

В случаях, когда полная сводимость не имеет места, необходимо понять, как неразложимые представления могут быть построены из неприводимых представлений как расширений фактора по подпредставлению.

Тензорные произведения представлений

Основная статья: Тензорное произведение представлений

Предполагать $\phi _{1}:G\rightarrow \mathrm {GL} (V_{1})$ и $\phi _{2}:G\rightarrow \mathrm {GL} (V_{2})$ являются представителями группы $G$. Тогда мы можем сформировать представление $\phi _{1}\otimes \phi _{2}$ группы G, действующей на тензорного произведения векторное пространство $V_{1}\otimes V_{2}$ следующее:

$(\phi _{1}\otimes \phi _{2})(g)=\phi _{1}(g)\otimes \phi _{2}(g)$.

Если $\phi _{1}$ и $\phi _{2}$ являются представлениями алгебры Ли, то правильная формула:

$(\phi _{1}\otimes \phi _{2})(X)=\phi _{1}(X)\otimes I+I\otimes \phi _{2}(X)$.

Это произведение можно признать копроизведением на коалгебре . В общем, тензорное произведение неприводимых представлений не является неприводимым; процесс разложения тензорного произведения в прямую сумму неприводимых представлений известен как теория Клебша – Гордана .

В случае теории представлений группы SU(2) (или, что то же самое, ее комплексифицированной алгебры Ли $\mathrm {sl} (2;\mathbb {C} )$), разложение легко провести. Неприводимые представления помечаются параметром $l$это неотрицательное целое число или полуцелое число; тогда представление имеет размерность $2l+1$. Предположим, мы берем тензорное произведение представления двух представлений с метками $l_{1}$ и $l_{2},$ где мы предполагаем $l_{1}\geq l_{2}$. Затем тензорное произведение разлагается как прямая сумма одной копии каждого представления с меткой $l$, где $l$ варьируется от $l_{1}-l_{2}$ к $l_{1}+l_{2}$ с шагом 1. Если, например, $l_{1}=l_{2}=1$, то значения $l$ которые встречаются, равны 0, 1 и 2. Таким образом, представление тензорного произведения размерности $(2l_{1}+1)\times (2l_{2}+1)=3\times 3=9$ разлагается как прямая сумма одномерного представления $(l=0),$ трехмерное представление $(l=1),$ и пятимерное представление $(l=2)$.

Отрасли и темы

См. также: Представление группы

Теория представлений отличается количеством разветвлений и разнообразием подходов к изучению представлений групп и алгебр. Хотя все теории имеют общие базовые концепции, которые уже обсуждались, они существенно различаются в деталях. Различия как минимум в 3 раза:

1. Теория представлений зависит от типа представляемого алгебраического объекта. Существует несколько различных классов групп, ассоциативных алгебр и алгебр Ли, и все их теории представлений имеют индивидуальный оттенок.
2. Теория представлений зависит от природы векторного пространства, в котором представлен алгебраический объект. Наиболее важное различие между конечномерными и бесконечномерными представлениями. В бесконечномерном случае важны дополнительные структуры (например, является ли пространство гильбертовым , банаховым и т. д.). Дополнительные алгебраические структуры могут быть наложены и в конечномерном случае.
3. Теория представлений зависит от типа поля , над которым определяется векторное пространство. Наиболее важными случаями являются поле комплексных чисел, поле действительных чисел, конечные поля и поля p-адических чисел . Дополнительные трудности возникают для полей положительной характеристики и для полей, не алгебраически незамкнутых .

Конечные группы

Основная статья: Представление конечной группы

Представления групп — очень важный инструмент в изучении конечных групп. Они также возникают в приложениях теории конечных групп к геометрии и кристаллографии . Представления конечных групп обладают многими чертами общей теории и указывают путь к другим разделам и темам теории представлений.

Над полем нулевой характеристики представление конечной группы G обладает рядом удобных свойств. Во-первых, представления группы G полупросты (вполне приводимы). Это следствие теоремы Машке , которая утверждает, что любое подпредставление V G - представления W имеет G -инвариантное дополнение. Одним из доказательств является выбор любой проекции π из W в V и замена ее средним значением π _G , определяемым формулой

$\pi _{G}(x)={\frac {1}{|G|}}\sum _{g\in G}g\cdot \pi (g^{-1}\cdot x).$

π _G эквивариантен, и его ядро ​​является искомым дополнением.

Конечномерные G- представления можно понять с помощью теории характеров : характер представления φ : G → GL( V ) — это функция класса χ _φ : G → F , определенная формулой

$\chi _{\varphi }(g)=\mathrm {Tr} (\varphi (g))$

где $\mathrm {Tr}$это след . Неприводимое представление группы G полностью определяется ее характером.

Теорема Машке в более общем смысле справедлива для полей p , таких как конечные поля , пока простое число p просто взаимно с порядком G. положительной характеристики Когда р и | г | имеют общий множитель , существуют G -представления, не являющиеся полупростыми, которые изучаются в подветви, называемой модулярной теорией представлений .

Методы усреднения также показывают, что если F — действительные или комплексные числа, то любое G -представление сохраняет скалярный продукт. $\langle \cdot ,\cdot \rangle$ на V в том смысле, что

$\langle g\cdot v,g\cdot w\rangle =\langle v,w\rangle$

для g в G и v , w в W. всех Следовательно, любое G -представление унитарно .

Унитарные представления автоматически полупросты, поскольку результат Машке можно доказать, взяв ортогональное дополнение к подпредставлению. При изучении представлений групп, которые не являются конечными, унитарные представления дают хорошее обобщение вещественных и комплексных представлений конечной группы.

Такие результаты, как теорема Машке и свойство унитарности, основанные на усреднении, можно обобщить на более общие группы, заменив среднее значение интегралом, при условии, что можно определить подходящее понятие интеграла. Это можно сделать для компактных топологических групп (включая компактные группы Ли), используя меру Хаара , и полученная теория известна как абстрактный гармонический анализ .

Над произвольными полями другим классом конечных групп, имеющим хорошую теорию представлений, являются конечные группы лиева типа . Важными примерами являются линейные алгебраические группы над конечными полями. Теория представлений линейных алгебраических групп и групп Ли распространяет эти примеры на бесконечномерные группы, причем последние тесно связаны с представлениями алгебры Ли . Важность теории характеров для конечных групп имеет аналог в теории весов для представлений групп и алгебр Ли.

Представления конечной группы G также напрямую связаны с представлениями алгебры через групповую алгебру F [ G ], которая представляет собой векторное пространство над F с элементами G в качестве базиса, оснащенное операцией умножения, определяемой групповой операцией линейности. и требование коммутации групповой операции и скалярного умножения.

Модульные представления

Основная статья: Модульная теория представлений

Модульные представления конечной группы G — это представления над полем, характеристика которого не взаимно проста с | G |, так что теорема Машке больше не справедлива (поскольку | G | не обратима в F и поэтому на нее нельзя делить). Тем не менее Рихард Брауэр распространил большую часть теории характеров на модульные представления, и эта теория сыграла важную роль на раннем этапе классификации конечных простых групп , особенно для простых групп, характеристика которых не поддавалась чисто теоретико-групповым методам, поскольку их силовские 2 -подгруппы были «слишком малы».

Помимо применения к теории групп, модульные представления естественным образом возникают в других разделах математики , таких как алгебраическая геометрия , теория кодирования , комбинаторика и теория чисел .

Унитарные представления

Основная статья: Унитарное представительство

Унитарное представление группы G — это линейное представление φ группы G в вещественном или (обычно) комплексном гильбертовом пространстве V такое, что ( g ) — унитарный оператор для каждого g ∈ G. φ Подобные представления стали широко применяться в квантовой механике с 1920-х годов, в частности, благодаря влиянию Германа Вейля , и это вдохновило развитие теории, в первую очередь благодаря анализу представлений группы Пуанкаре Юджином Вигнером . Одним из пионеров построения общей теории унитарных представлений (для любой группы G , а не только для конкретных групп, полезных в приложениях) был Джордж Макки , а обширная теория была разработана Хариш-Чандрой и другими в 1950-х и 1960-х годах.

Основная цель — описать « унитарно-двойственное , пространство неприводимых унитарных представлений G. » Теория наиболее развита в случае, когда G — локально компактная (хаусдорфова) топологическая группа и представления сильно непрерывны . Для G абелева унитарное двойственное представление - это просто пространство характеров , а для G компактного теорема Питера – Вейля показывает, что неприводимые унитарные представления конечномерны, а унитарное двойственное представление дискретно. Например, если G — группа окружностей S ¹ , тогда символы задаются целыми числами, а унитарным двойником является Z .

Для некомпактного G вопрос о том, какие представления являются унитарными, является тонким. Хотя неприводимые унитарные представления должны быть «допустимыми» (как модули Хариш-Чандры ) и легко определить, какие допустимые представления имеют невырожденную инвариантную полуторалинейную форму , трудно определить, когда эта форма является положительно определенной. Эффективное описание унитарно-двойственной группы, даже для относительно благополучных групп, таких как вещественные редуктивные группы Ли (обсуждаемые ниже), остается важной открытой проблемой теории представлений. Она была решена для многих конкретных групп, таких как SL(2, R ) и группа Лоренца .

Гармонический анализ

Основная статья: Абстрактный гармонический анализ

Двойственность между группой кругов S ¹ и целые числа Z или, в более общем смысле, между тором T ^н и З ^н хорошо известна в анализе как теория рядов Фурье , а преобразование Фурье аналогичным образом выражает тот факт, что пространство символов в реальном векторном пространстве является двойственным векторным пространством . Таким образом, теория унитарного представления и гармонический анализ тесно связаны, и абстрактный гармонический анализ использует эту связь, развивая анализ функций на локально компактных топологических группах и связанных с ними пространствах.

Основная цель состоит в том, чтобы предоставить общую форму преобразования Фурье и теоремы Планшереля . Это делается путем построения меры на унитарном двойственном элементе и изоморфизма между регулярным представлением группы G в пространстве L ² ( G ) функций , суммируемых с квадратом на G , и ее представление в пространстве L ² функции на унитарном двойственном. Двойственность Понтрягина и теорема Питера – Вейля достигают этого для абелевой и компактной G соответственно.

Другой подход предполагает рассмотрение всех унитарных представлений, а не только неприводимых. Они образуют категорию , а двойственность Таннаки–Крейна позволяет восстановить компактную группу из ее категории унитарных представлений.

Если группа не является ни абелевой, ни компактной, не известна общая теория с аналогом теоремы Планшереля или обращения Фурье, хотя Александр Гротендик расширил двойственность Таннаки-Крейна на связь между линейными алгебраическими группами и таннаковскими категориями .

Гармонический анализ также был расширен от анализа функций в группе G до функций в однородных пространствах для G . Теория особенно хорошо развита для симметричных пространств и дает теорию автоморфных форм (обсуждаемых ниже).

Группы лжи

Основная статья: Представление группы Ли

Группа Ли — это группа, которая также является гладким многообразием . Многие классические группы матриц над действительными или комплексными числами являются группами Ли. Многие из групп, важных в физике и химии, являются группами Ли, и их теория представлений имеет решающее значение для применения теории групп в этих областях.

Теорию представлений групп Ли можно сначала разработать, рассмотрев компактные группы, к которым применимы результаты теории компактных представлений. Эту теорию можно распространить на конечномерные представления полупростых групп Ли, используя унитарный прием Вейля : каждая полупростая вещественная группа Ли G имеет комплексификацию, которая представляет собой комплексную группу Ли G. ^с , и эта комплексная группа Ли имеет максимальную компактную подгруппу K . Конечномерные представления G близко соответствуют представлениям K .

Общая группа Ли — это полупрямое произведение и разрешимой группы Ли полупростой группы Ли ( разложение Леви ). Классификация представлений разрешимых групп Ли вообще сложна, но в практических случаях часто проста. Представления полупрямых произведений затем можно анализировать с помощью общих результатов, называемых теорией Макки , которая является обобщением методов, используемых в классификации Вигнером представлений группы Пуанкаре.

Алгебры Ли

Основная статья: Представление алгебры Ли

Алгебра Ли над полем F — это векторное пространство над F, снабженное кососимметричной билинейной операцией , называемой скобкой Ли , которая удовлетворяет тождеству Якоби . Алгебры Ли возникают, в частности, как касательные пространства к группам Ли в единичном элементе , что приводит к их интерпретации как «бесконечно-зимальные симметрии». Важным подходом к теории представлений групп Ли является изучение соответствующей теории представлений алгебр Ли, но представления алгебр Ли также представляют интерес.

Алгебры Ли, как и группы Ли, имеют разложение Леви на полупростые и разрешимые части, при этом теория представлений разрешимых алгебр Ли в целом трудноразрешима. Напротив, конечномерные представления полупростых алгебр Ли полностью поняты после работы Эли Картана . Представление полупростой алгебры Ли 𝖌 анализируется путем выбора подалгебры Картана , которая по существу является общей максимальной подалгеброй 𝖍 𝖌, на которой скобка Ли равна нулю («абелева»). Представление 𝖌 можно разложить на весовые пространства , которые являются собственными пространствами для действия 𝖍 и бесконечно малого аналога символов. Структура полупростых алгебр Ли тогда сводит анализ представлений к легко понимаемой комбинаторике возможных весов, которые могут возникнуть.

Бесконечномерные

Смотрите также: Аффинная алгебра Ли и алгебра Каца – Муди.

Существует много классов бесконечномерных алгебр Ли, представления которых изучены. Среди них важным классом являются алгебры Каца–Муди. Они названы в честь Виктора Каца и Роберта Муди , которые их независимо открыли. Эти алгебры образуют обобщение конечномерных полупростых алгебр Ли и разделяют многие из их комбинаторных свойств. Это означает, что у них есть класс представлений, которые можно понимать так же, как представления полупростых алгебр Ли.

Аффинные алгебры Ли — частный случай алгебр Каца–Муди, имеющих особое значение в математике и теоретической физике , особенно в конформной теории поля и теории точно решаемых моделей . Кац обнаружил элегантное доказательство некоторых комбинаторных тождеств, тождеств Макдональда , которое основано на теории представлений аффинных алгебр Каца – Муди.

Супералгебры Ли

Основная статья: Представление супералгебры Ли

Супералгебры Ли являются обобщениями алгебр Ли, в которых базовое векторное пространство имеет Z ₂ -градуировку, а свойства кососимметрии и тождества Якоби скобки Ли изменяются знаками. Их теория представлений аналогична теории представлений алгебр Ли.

Линейные алгебраические группы

Смотрите также: Линейная алгебраическая группа

Линейные алгебраические группы (или, в более общем смысле, аффинные групповые схемы ) являются аналогами в алгебраической геометрии групп Ли , но над более общими полями, чем R или C. просто В частности, над конечными полями они порождают конечные группы лиева типа . Хотя линейные алгебраические группы имеют классификацию, очень похожую на классификацию групп Ли, их теория представлений довольно отличается (и гораздо менее хорошо понята) и требует других методов, поскольку топология Зарисского относительно слаба, и методы анализа больше не используются. доступный.

Инвариантная теория

Основная статья: Теория инвариантов

Теория инвариантов изучает действия на алгебраических многообразиях с точки зрения их влияния на функции, образующие представления группы. Классически теория занималась вопросом явного описания полиномиальных функций , которые не изменяются или являются инвариантными при преобразованиях из заданной линейной группы . Современный подход анализирует разложение этих представлений на неприводимые.

Теория инвариантов бесконечных групп неразрывно связана с развитием линейной алгебры , особенно теорий квадратичных форм и определителей . Еще одним предметом с сильным взаимным влиянием является проективная геометрия , где для организации предмета может использоваться теория инвариантов, а в 1960-е годы новую жизнь в этот предмет вдохнул Дэвид Мамфорд в форме его геометрической теории инвариантов .

Теория представлений полупростых групп Ли уходит корнями в теорию инвариантов. а прочные связи между теорией представлений и алгебраической геометрией имеют множество параллелей в дифференциальной геометрии, начиная с Феликса Кляйна и Эрлангенской программы связей Картана , Эли которые помещают группы и симметрию в центр геометрии. Современные разработки связывают теорию представлений и теорию инвариантов с такими разнообразными областями, как голономия , дифференциальные операторы и теория нескольких комплексных переменных .

Автоморфные формы и теория чисел

Основная статья: Автоморфная форма

Автоморфные формы — это обобщение модульных форм на более общие аналитические функции , возможно, нескольких комплексных переменных , с аналогичными свойствами преобразования. Обобщение включает замену модулярной группы PSL ₂ ( R ) и выбранной конгруэнц-подгруппы полупростой группой Ли G и дискретной подгруппой Γ . Подобно тому, как модульные формы можно рассматривать как дифференциальные формы на факторе верхнего полупространства H = PSL ₂ ( R )/SO(2), автоморфные формы можно рассматривать как дифференциальные формы (или подобные объекты) на Γ \ G / K. , где K (обычно) максимальная компактная подгруппа группы G . Однако требуется некоторая осторожность, поскольку частное обычно имеет особенности. Фактор полупростой группы Ли по компактной подгруппе является симметрическим пространством , и поэтому теория автоморфных форм тесно связана с гармоническим анализом симметричных пространств.

До разработки общей теории были подробно разработаны многие важные частные случаи, в том числе модулярные формы Гильберта и модулярные формы Зигеля . Важные результаты в теории включают формулу следов Сельберга и осознание Робертом Ленглендсом того, что теорема Римана-Роха может быть применена для вычисления размерности пространства автоморфных форм. Последующее понятие «автоморфного представления» оказалось очень полезным для случая, когда G — алгебраическая группа , рассматриваемая как адельная алгебраическая группа . В результате целая философия программы Ленглендса сложилась вокруг связи между представлением и теоретико-числовыми свойствами автоморфных форм.

Ассоциативные алгебры

Основная статья: Алгебраическое представление

В каком-то смысле представления ассоциативной алгебры обобщают как представления групп, так и алгебр Ли. Представление группы индуцирует представление соответствующего группового кольца или групповой алгебры , а представления алгебры Ли биективно соответствуют представлениям ее универсальной обертывающей алгебры . Однако теория представлений общих ассоциативных алгебр не обладает всеми прекрасными свойствами теории представлений групп и алгебр Ли.

Теория модулей

Основная статья: Теория модулей

Рассматривая представления ассоциативной алгебры, можно забыть о базовом поле и просто рассматривать ассоциативную алгебру как кольцо, а ее представления как модули. Этот подход удивительно плодотворен: многие результаты теории представлений можно интерпретировать как частные случаи результатов о модулях над кольцом.

Алгебры Хопфа

Основная статья: Теория представлений алгебр Хопфа

Алгебры Хопфа позволяют улучшить теорию представлений ассоциативных алгебр, сохраняя при этом теорию представлений групп и алгебр Ли как особые случаи. В частности, тензорное произведение двух представлений является представлением, как и двойственное векторное пространство.

Алгебры Хопфа, связанные с группами, имеют структуру коммутативной алгебры, поэтому общие алгебры Хопфа известны как квантовые группы , хотя этот термин часто ограничивается некоторыми алгебрами Хопфа, возникающими как деформации групп или их универсальные обертывающие алгебры. Теория представлений квантовых групп добавила удивительные идеи к теории представлений групп Ли и алгебр Ли, например, благодаря кристаллическому базису Кашивары.

Обобщения

Теоретико-множественные представления

Основная статья: Групповое действие (математика)

Теоретико -множественное представление (также известное как групповое действие или представление перестановок ) группы G на множестве X задается функцией ρ из G в X. ^Икс , набор функций g от X до X , таких, что для всех 1 _, g 2 _в G и всех x в X :

$\rho (1)[x]=x$

$\rho (g_{1}g_{2})[x]=\rho (g_{1})[\rho (g_{2})[x]].$

Из этого условия и аксиом группы следует, что ( g ) является биекцией (или перестановкой ) для всех g в G. ρ Таким образом, мы можем эквивалентно определить представление перестановки как гомоморфизм группы из G в симметрическую группу S _X группы X .

Представительства в других категориях

См. Также: Теория категорий

Каждую группу G можно рассматривать как категорию с одним объектом; морфизмы в этой категории — это просто элементы G . произвольной C представление ​ G G в C является функтором из в категории C. Для Такой функтор выбирает объект в C и групповой гомоморфизм из G в Aut( X ), группу X. X автоморфизмов

В случае, когда C — это Vect _F , категория векторных пространств над полем F , это определение эквивалентно линейному представлению. Аналогично, теоретико-множественное представление — это просто представление G в категории множеств .

В качестве другого примера рассмотрим категорию топологических . Top пространств Представления в Top — это гомоморфизмы из G в группу гомеоморфизмов топологического X. пространства

Три типа представлений, тесно связанных с линейными представлениями:

• Проективные представления : в категории проективных пространств . Их можно описать как «линейные представления с точностью до скалярных преобразований».
• аффинные представления : в категории аффинных пространств . Например, евклидова группа действует аффинно в евклидовом пространстве .
• копредставления унитарных и антиунитарных групп : в категории комплексных векторных пространств с морфизмами, являющимися линейными или антилинейными преобразованиями.

Представления категорий

Смотрите также: Колчан (математика)

Поскольку группы являются категориями, можно также рассмотреть представление других категорий. Простейшее обобщение относится к моноидам , которые представляют собой категории с одним объектом. Группы — это моноиды, для которых любой морфизм обратим. Общие моноиды имеют представления в любой категории. В категории множеств это моноидные действия , но можно изучать моноидные представления на векторных пространствах и других объектах.

В более общем плане можно ослабить предположение, что представляемая категория имеет только один объект. В полной общности это просто теория функторов между категориями, и мало что можно сказать.

Один особый случай оказал существенное влияние на теорию представлений, а именно теорию представлений колчанов. Колчан — это просто ориентированный граф (с разрешенными петлями и несколькими стрелками), но его можно превратить в категорию (а также в алгебру), рассматривая пути в графе. Представления таких категорий/алгебр пролили свет на некоторые аспекты теории представлений, например, позволив в некоторых случаях свести неполупростые вопросы теории представлений о группе к полупростым вопросам теории представлений о колчане.

См. также

• Представление Галуа
• Глоссарий теории представлений
• Представительство группы
• Это теория
• Список тем теории представлений
• Список тем гармонического анализа
• Численный анализ
• Философия форм возврата
• Представление (математика)
• Теорема о представлении
• Универсальная алгебра

Ссылки

• Альперин, Дж. Л. (1986), Теория локальных представлений: модульные представления как введение в локальную теорию представлений конечных групп , Cambridge University Press, ISBN  978-0-521-44926-7 .
• Баргманн, В. (1947), «Неприводимые унитарные представления группы Лоренца», Annals of Mathematics , 48 ​​(3): 568–640, doi : 10.2307/1969129 , JSTOR   1969129 .
• Борель, Арманд (2001), Очерки истории групп Ли и алгебраических групп , Американское математическое общество, ISBN  978-0-8218-0288-5 .
• Борель, Арманд; Кассельман, В. (1979), Автоморфные формы, представления и L-функции , Американское математическое общество, ISBN  978-0-8218-1435-2 .
• Кертис, Чарльз В .; Райнер, Ирвинг (1962), Теория представлений конечных групп и ассоциативных алгебр , John Wiley & Sons (переиздание 2006 г., книжный магазин AMS), ISBN  978-0-470-18975-7 .
• Фолланд, Джеральд Б. (1995), Курс абстрактного гармонического анализа , CRC Press, ISBN  978-0-8493-8490-5 .
• Фултон, Уильям ; Харрис, Джо (1991). Теория представлений. Первый курс . Тексты для аспирантов по математике , Чтения по математике. Том. 129. Нью-Йорк: Springer-Verlag. дои : 10.1007/978-1-4612-0979-9 . ISBN  978-0-387-97495-8 . МР   1153249 . OCLC   246650103 . .
• Гелбарт, Стивен (1984), «Элементарное введение в программу Ленглендса», Бюллетень Американского математического общества , 10 (2): 177–219, doi : 10.1090/S0273-0979-1984-15237-6 .
• Гудман, Роу; Уоллах, Нолан Р. (1998), Представления и инварианты классических групп , Cambridge University Press, ISBN  978-0-521-66348-9 .
• Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для аспирантов по математике, том. 222 (2-е изд.), Спрингер, ISBN  978-3319134666
• Хельгасон, Сигурдур (1978), Дифференциальная геометрия, группы Ли и симметричные пространства , Academic Press, ISBN  978-0-12-338460-7
• Хамфрис, Джеймс Э. (1972a), Введение в алгебры Ли и теорию представлений , Биркхойзер, ISBN  978-0-387-90053-7 .
• Хамфрис, Джеймс Э. (1972b), Линейные алгебраические группы , Тексты для аспирантов по математике, том. 21, Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-0-387-90108-4 , МР   0396773
• Джеймс, Гордон; Либек, Мартин (1993), Представления и характеры групп , Кембридж: Издательство Кембриджского университета, ISBN  978-0-521-44590-0 .
• Янцен, Йенс Карстен (2003), Представления алгебраических групп , Американское математическое общество, ISBN  978-0-8218-3527-2 .
• Кац, Виктор Г. (1977), «Супералгебры Ли», Успехи в математике , 26 (1): 8–96, doi : 10.1016/0001-8708(77)90017-2 .
• Кац, Виктор Г. (1990), Бесконечномерные алгебры Ли (3-е изд.), Cambridge University Press, ISBN  978-0-521-46693-6 .
• Ким, Шун Кён (1999), Теоретико-групповые методы и приложения к молекулам и кристаллам: и приложения к молекулам и кристаллам , Cambridge University Press, ISBN  978-0-521-64062-6 .
• Кнапп, Энтони В. (2001), Теория представлений полупростых групп: обзор, основанный на примерах , Princeton University Press, ISBN  978-0-691-09089-4 .
• Кострикин А.И. ; Манин, Юрий И. (1997), Линейная алгебра и геометрия , Тейлор и Фрэнсис, ISBN  978-90-5699-049-7 .
• Лам, Тай (1998), «Представления конечных групп: сто лет», Уведомления AMS , 45 (3, 4): 361–372 (Часть I) , 465–474 (Часть II) .
• Любич, Юрий И. (1988). Введение в теорию банаховых представлений групп . Теория операторов: достижения и приложения. Том. 30. Базель: Биркхаузер. ISBN  978-3-7643-2207-6 .
• Мамфорд, Дэвид ; Фогарти, Дж.; Кирван, Ф. (1994), Геометрическая теория инвариантов , Результаты по математике и смежным областям (2) [Результаты по математике и смежным областям (2)], том. 34 (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN  978-3-540-56963-3 , МР   0214602 ; МИСТЕР 0719371 (2-е изд.); МИСТЕР 1304906 (3-е изд.)
• Олвер, Питер Дж. (1999), Классическая теория инвариантов , Кембридж: Издательство Кембриджского университета, ISBN  978-0-521-55821-1 .
• Питер, Ф.; Вейль, Герман (1927), «Полнота примитивных представлений замкнутой непрерывной группы», Mathematical Annals , 97 (1): 737–755, doi : 10.1007/BF01447892 , S2CID   120013521 .
• Понтрягин, Лев С. (1934), «Теория топологических коммутативных групп», Annals of Mathematics , 35 (2): 361–388, doi : 10.2307/1968438 , JSTOR   1968438 .
• Салли, Пол ; Воган, Дэвид А. (1989), Теория представлений и гармонический анализ полупростых групп Ли , Американское математическое общество, ISBN  978-0-8218-1526-7 .
• Серр, Жан-Пьер (1977), Линейные представления конечных групп , Springer-Verlag, ISBN  978-0387901909 .
• Шарп, Ричард В. (1997), Дифференциальная геометрия: обобщение Картаном программы Эрлангена Кляйна , Springer, ISBN  978-0-387-94732-7 .
• Симсон, Дэниел; Сковронский, Анджей; Асем, Ибрагим (2007), Элементы теории представлений ассоциативных алгебр , Cambridge University Press, ISBN  978-0-521-88218-7 .
• Штернберг, Шломо (1994), Теория групп и физика , издательство Кембриджского университета, ISBN  978-0-521-55885-3 .
• Тунг, Ву-Ки (1985). Теория групп в физике (1-е изд.). Нью-Джерси·Лондон·Сингапур·Гонконг: World Scientific . ISBN  978-9971966577 .
• Вейль, Герман (1928), Теория групп и квантовая механика (Теория групп и квантовая механика, перевод HP Робертсона, изд. 1931 г.), С. Хирцель, Лейпциг (перепечатано в 1950 г., Дувр), ISBN  978-0-486-60269-1 .
• Вейль, Герман (1946), Классические группы: их инварианты и представления (2-е изд.), Princeton University Press (перепечатано в 1997 г.), ISBN  978-0-691-05756-9 .
• Вигнер, Юджин П. (1939), «Об унитарных представлениях неоднородной группы Лоренца», Annals of Mathematics , 40 (1): 149–204, Бибкод : 1939AnMat..40..149W , doi : 10.2307/1968551 , JSTOR   1968551 , S2CID   121773411 .

Внешние ссылки

• «Теория представлений» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Александр Кириллов-младший , Введение в группы Ли и алгебры Ли (2008). Учебник, предварительную версию pdf можно скачать с домашней страницы автора.
• Кевин Хартнетт (2020), статья о теории представлений в журнале Quanta