Аффинная алгебра Ли

В математике аффинная алгебра Ли — это бесконечномерная алгебра Ли , построенная каноническим образом из конечномерной простой алгебры Ли . Учитывая аффинную алгебру Ли, можно также сформировать связанную с ней аффинную алгебру Каца-Муди, как описано ниже. С чисто математической точки зрения аффинные алгебры Ли интересны тем, что их теория представлений , как и теория представлений конечномерных полупростых алгебр Ли , гораздо лучше понятна, чем теория общих алгебр Каца – Муди. Как заметил Виктор Кац , формула характера для представлений аффинных алгебр Ли подразумевает определенные комбинаторные тождества, тождества Макдональда .

Аффинные алгебры Ли играют важную роль в теории струн и двумерной конформной теории поля благодаря способу их построения: начиная с простой алгебры Ли. ${\mathfrak {g}}$, рассматривается алгебра петель , $L{\mathfrak {g}}$, образованный ${\mathfrak {g}}$-значные функции на окружности (интерпретируемой как замкнутая струна) с поточечным коммутатором. Аффинная алгебра Ли ${\hat {\mathfrak {g}}}$ получается добавлением к петлевой алгебре одного дополнительного измерения и нетривиальной модификацией коммутатора, который физики называют квантовой аномалией (в данном случае аномалией модели WZW ), а математики — центральным расширением . В более общем смысле, если σ — автоморфизм простой алгебры Ли ${\mathfrak {g}}$ ассоциированная с автоморфизмом ее диаграммы Дынкина , алгебра витых петель $L_{\sigma }{\mathfrak {g}}$ состоит из ${\mathfrak {g}}$-значные функции f на вещественной прямой, удовлетворяющиеусловие скрученной периодичности ж ( Икс + 2 π ) знак равно σ ж ( Икс ) . Их центральными расширениями являются в точности скрученные аффинные алгебры Ли . Точка зрения теории струн помогает понять многие глубокие свойства аффинных алгебр Ли, такие как тот факт, что характеры их представлений преобразуются между собой под действием модулярной группы .

Аффинные алгебры Ли из простых алгебр Ли

Определение

Если ${\mathfrak {g}}$ — конечномерная простая алгебра Ли, соответствующая аффинная алгебра Ли ${\hat {\mathfrak {g}}}$ строится как центральное расширение алгебры петель ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$, с одномерным центром $\mathbb {\mathbb {C} } c.$В качестве векторного пространства

${\widehat {\mathfrak {g}}}={\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]\oplus \mathbb {\mathbb {C} } c,$

где $\mathbb {\mathbb {C} } [t,t^{-1}]$ — комплексное векторное пространство полиномов Лорана от неопределенного t . Скобка Ли определяется по формуле

$[a\otimes t^{n}+\alpha c,b\otimes t^{m}+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta _{m+n,0}c$

для всех $a,b\in {\mathfrak {g}},\alpha ,\beta \in \mathbb {\mathbb {C} }$ и $n,m\in \mathbb {Z}$, где $[a,b]$ — скобка Ли в алгебре Ли ${\mathfrak {g}}$ и $\langle \cdot |\cdot \rangle$ это форма Картана-Киллинга на ${\mathfrak {g}}.$

Аффинная алгебра Ли, соответствующая конечномерной полупростой алгебре Ли, представляет собой прямую сумму аффинных алгебр Ли, соответствующих ее простым слагаемым. Существует выдающийся вывод аффинной алгебры Ли, определяемой формулой

$\delta (a\otimes t^{m}+\alpha c)=t{d \over dt}(a\otimes t^{m}).$

Соответствующая аффинная алгебра Каца – Муди определяется как полупрямое произведение путем добавления дополнительного генератора d, который удовлетворяет условию [ d , A ] = δ ( A ).

Построение диаграмм Дынкина

Диаграмма Дынкина каждой аффинной алгебры Ли состоит из диаграммы соответствующей простой алгебры Ли плюс дополнительный узел, который соответствует добавлению мнимого корня. Конечно, такой узел не может быть присоединен к диаграмме Дынкина в любом месте, но для каждой простой алгебры Ли существует число возможных присоединений, равное мощности группы внешних автоморфизмов алгебры Ли. В частности, эта группа всегда содержит единицу, а соответствующая аффинная алгебра Ли называется раскрученной аффинной алгеброй Ли. Когда простая алгебра допускает автоморфизмы, не являющиеся внутренними автоморфизмами, можно получить другие диаграммы Дынкина, соответствующие скрученным аффинным алгебрам Ли.

Диаграммы Дынкина для аффинных алгебр Ли

Набор расширенных (раскрученных) аффинных диаграмм Дынкина с добавленными узлами, выделенными зеленым цветом.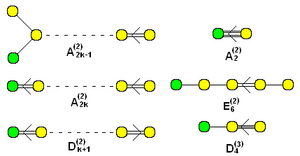

«Искаженные» аффинные формы имеют надстрочные индексы (2) или (3). ( k — количество узлов в графе)

Классификация центральных расширений

Присоединение дополнительного узла к диаграмме Дынкина соответствующей простой алгебры Ли соответствует следующей конструкции. Аффинную алгебру Ли всегда можно построить как центральное расширение алгебры петель соответствующей простой алгебры Ли. Если вместо этого кто-то хочет начать с полупростой алгебры Ли, то необходимо централизованно расширить его на количество элементов, равное числу простых компонентов полупростой алгебры. Вместо этого в физике часто рассматривают прямую сумму полупростой алгебры и абелевой алгебры. $\mathbb {\mathbb {C} } ^{n}$. В этом случае также необходимо добавить еще n центральных элементов для n абелевых образующих.

Вторая целая когомология группы петель соответствующей простой компактной группы Ли изоморфна целым числам. Центральные расширения аффинной группы Ли с помощью одного образующего представляют собой топологически расслоения окружностей над этой группой свободных петель, которые классифицируются по двум классам, известным как первый Черна расслоения класс . Поэтому центральные расширения аффинной группы Ли классифицируются по одному параметру k называется уровнем , который в физической литературе, где он впервые появился, . Унитарные представления аффинных компактных групп со старшим весом существуют только тогда, когда k — натуральное число. В более общем смысле, если рассматривать полупростую алгебру, у каждого простого компонента есть центральный заряд.

Структура

Базис Картана – Вейля

Как и в конечном случае, определение базиса Картана–Вейля является важным шагом в определении структуры аффинных алгебр Ли.

Исправьте конечномерную простую комплексную алгебру Ли. ${\mathfrak {g}}$ с подалгеброй Картана ${\mathfrak {h}}$ и особая корневая система $\Delta$. Знакомство с обозначениями $X_{n}=X\otimes t^{n},$, можно попытаться расширить базис Картана–Вейля $\{H^{i}\}\cup \{E^{\alpha }|\alpha \in \Delta \}$ для ${\mathfrak {g}}$ единице для аффинной алгебры Ли, заданной формулой $\{H_{n}^{i}\}\cup \{c\}\cup \{E_{n}^{\alpha }\}$, с $\{H_{0}^{i}\}\cup \{c\}$ образуя абелеву подалгебру.

Собственные значения $ad(H_{0}^{i})$ и $ad(c)$ на $E_{n}^{\alpha }$ являются $\alpha ^{i}$ и $0$ соответственно и независимо от $n$. Поэтому корень $\alpha$ бесконечно вырождена относительно этой абелевой подалгебры. Добавление описанного выше вывода к абелевой подалгебре превращает абелеву подалгебру в подалгебру Картана для аффинной алгебры Ли с собственными значениями $(\alpha ^{1},\cdots ,\alpha ^{dim{\mathfrak {h}}},0,n)$ для $E_{n}^{\alpha }.$

Убийственная форма

Форму Киллинга можно почти полностью определить, используя ее свойство инвариантности. Используя обозначения $B$ для формы убийства на ${\mathfrak {g}}$ и ${\hat {B}}$ для формы Киллинга на аффинной алгебре Каца – Муди $${\hat {B}}(X_{n},Y_{m})=B(X,Y)\delta _{n+m,0},$$$${\hat {B}}(X_{n},c)=0,{\hat {B}}(X_{n},d)=0$$$${\hat {B}}(c,c)=0,{\hat {B}}(c,d)=1,{\hat {B}}(d,d)=0,$$где только последнее уравнение не фиксировано инвариантно, а выбрано по соглашению. Примечательно, что ограничение ${\hat {B}}$ к $c,d$ подпространство дает билинейную форму с сигнатурой $(+,-)$.

Напишите аффинный корень, связанный с $E_{n}^{\alpha }$ как ${\hat {\alpha }}=(\alpha ;0;n)$. Определение $\delta =(0,0,1)$, это можно переписать $${\hat {\alpha }}=\alpha +n\delta .$$

Полный набор корней $${\hat {\Delta }}=\{\alpha +n\delta |n\in \mathbb {Z} ,\alpha \in \Delta \}\cup \{n\delta |n\in \mathbb {Z} ,n\neq 0\}.$$Затем $\delta$ необычно, поскольку имеет нулевую длину: $(\delta ,\delta )=0$ где $(\cdot ,\cdot )$ – билинейная форма на корнях, индуцированная формой Киллинга.

Аффинный простой корень

Чтобы получить основу простых корней для аффинной алгебры, необходимо добавить дополнительный простой корень, который определяется выражением $$\alpha _{0}=-\theta +\delta$$где $\theta$ является высшим корнем ${\mathfrak {g}}$, используя обычное понятие высоты корня. Это позволяет определить расширенную матрицу Картана и расширенные диаграммы Дынкина .

Теория представлений

Теория представлений аффинных алгебр Ли обычно разрабатывается с использованием модулей Верма . Как и в случае полупростых алгебр Ли, это модули старшего веса . Конечномерных представлений не существует; это следует из того, что нулевые векторы конечномерного модуля Верма обязательно равны нулю; тогда как для аффинных алгебр Ли это не так. Грубо говоря, это следует из того, что форма Киллинга лоренцева в $c,\delta$ направления, таким образом $(z,{\bar {z}})$ иногда называются «координатами светового конуса» на строке. «Радиально упорядоченные» продукты текущего оператора можно понимать как нормально упорядоченные по времени, если принять $z=\exp(\tau +i\sigma )$ с $\tau$ времяподобное направление вдоль струнного мира и $\sigma$ пространственное направление.

Вакуумное представление ранга k

Более детально представления строятся следующим образом.

Исправить алгебру Ли ${\mathfrak {g}}$ и основа $\{J^{\rho }\}$. Затем $\{J_{n}^{\rho }\}=\{J^{\rho }\otimes t^{n}\}$ является базисом соответствующей алгебры петель, а $\{J_{n}^{\rho }\}\cup \{c\}$ является базисом аффинной алгебры Ли ${\hat {\mathfrak {g}}}$.

Вакуумное представление ранга $k$, обозначенный $V_{k}({\mathfrak {g}})$ где $k\in \mathbb {C}$ это комплексное представление с базисом $$\{v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}:n_{1}\geq \cdots \geq n_{m}\geq 1,\rho _{1}\leq \cdots \leq \rho _{m}\}\cup \{\Omega \}$$и определить действие ${\hat {\mathfrak {g}}}$ на $V=V_{k}({\mathfrak {g}})$ по (с $n>0$) $$c=k{\text{id}}_{V},\,J_{n}^{\rho }\Omega =0,$$$$J_{-n}^{\rho }\Omega =v_{n}^{\rho }\,J_{-n}^{\rho }v_{n_{1}\cdots n_{m}}^{\rho _{1}\cdots \rho _{m}}=v_{nn_{1}\cdots n_{m}}^{\rho \rho _{1}\cdots \rho _{m}}.$$

Аффинная вершинная алгебра

См. Также: Алгебра вершинных операторов § Пример: вакуумные модули WZW

Вакуумное представление фактически может быть оснащено структурой вершинной алгебры, и в этом случае оно называется аффинной вершинной алгеброй ранга $k$. Аффинная алгебра Ли естественным образом расширяется до алгебры Каца – Муди с дифференциалом $d$ в лице оператора перевода $T$ в вершинной алгебре.

Группа Вейля и персонажи

Основная статья: формула характера Вейля-Каца

Группу Вейля аффинной алгебры Ли можно записать как полупрямое произведение группы Вейля алгебры нулевой моды (алгебры Ли, используемой для определения алгебры петель ) и решетки кокорней .

Формула характера Вейля алгебраических характеров аффинных алгебр Ли обобщается до формулы характера Вейля-Каца . Из них следует ряд интересных конструкций. Можно построить обобщения тэта-функции Якоби . Эти тэта-функции преобразуются в модульную группу . Обычные тождества знаменателя полупростых алгебр Ли также обобщают; поскольку символы могут быть записаны как «деформации» или q-аналоги высших весов, это привело ко многим новым комбинаторным тождествам, включая многие ранее неизвестные тождества для эта-функции Дедекинда . Эти обобщения можно рассматривать как практический пример программы Ленглендса .

Приложения

Благодаря конструкции Сугавары универсальная обертывающая алгебра любой аффинной алгебры Ли имеет алгебру Вирасоро в качестве подалгебры. Это позволяет аффинным алгебрам Ли служить алгебрами симметрии конформных теорий поля, таких как модели WZW или модели смежных классов. Как следствие, аффинные алгебры Ли также появляются в описании теории струн на мировом листе .

Пример

Алгебра Гейзенберга определяется генераторами $a_{n},n\in \mathbb {Z}$ удовлетворяющие коммутационным соотношениям $$[a_{m},a_{n}]=m\delta _{m+n,0}c$$может быть реализована как аффинная алгебра Ли ${\hat {\mathfrak {u}}}(1)$.

Ссылки

• Фукс, Юрген (1992), Аффинные алгебры Ли и квантовые группы , Cambridge University Press, ISBN  0-521-48412-Х
• Годдард, Питер ; Олив, Дэвид (1988), Алгебры Каца-Муди и Вирасоро: Переиздание для физиков , Расширенная серия по математической физике, том. 3, Всемирный научный, ISBN  9971-5-0419-7
• Кац, Виктор (1990), Бесконечномерные алгебры Ли (3-е изд.), Cambridge University Press, ISBN  0-521-46693-8
• Коно, Тошитаке (1998), Конформная теория поля и топология , Американское математическое общество, ISBN  0-8218-2130-Х
• Прессли, Эндрю; Сигал, Грэм (1986), Группы циклов , Oxford University Press, ISBN  0-19-853535-Х