Модуль Верма

Модули Вермы , названные в честь Дайя-Нанда Вермы , — объекты теории представлений алгебр Ли , раздела математики .

Модули Вермы можно использовать при классификации неприводимых представлений комплексной полупростой алгебры Ли. В частности, хотя модули Верма сами по себе являются бесконечномерными, их факторы можно использовать для построения конечномерных представлений с наибольшим весом. $\lambda$ , где $\lambda$ является доминирующим и целостным. ^[1] Их гомоморфизмы соответствуют инвариантным дифференциальным операторам над многообразиями флагов .

Неформальное строительство [ править ]

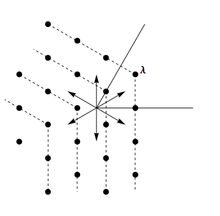
Мы можем объяснить идею модуля Verma следующим образом. ^[2] Позволять ${\mathfrak {g}}$ — полупростая алгебра Ли (над $\mathbb {C}$ , для простоты). Позволять ${\mathfrak {h}}$ — фиксированная подалгебра Картана в ${\mathfrak {g}}$ и пусть $R$ быть связанной корневой системой. Позволять $R^{+}$ — фиксированный набор положительных корней. Для каждого $\alpha \in R^{+}$ , выберите ненулевой элемент $X_{\alpha }$ для соответствующего корневого пространства ${\mathfrak {g}}_{\alpha }$ и ненулевой элемент $Y_{\alpha }$ в корневом пространстве ${\mathfrak {g}}_{-\alpha }$ . Мы думаем о $X_{\alpha }$ 's как "повышение операторов" и $Y_{\alpha }$ как "опускание операторов".

Теперь позвольте $\lambda \in {\mathfrak {h}}^{*}$ быть произвольным линейным функционалом, не обязательно доминирующим или целым. Наша цель — построить представление $W_{\lambda }$ из ${\mathfrak {g}}$ с наибольшим весом $\lambda$ который генерируется одним ненулевым вектором $v$ с весом $\lambda$ . Модуль Верма — это один из таких модулей с наибольшим весом, который является максимальным в том смысле, что любой другой модуль с наибольшим весом $\lambda$ является фактором модуля Верма. Окажется, что модули Верма всегда бесконечномерны; если $\lambda$ является доминантным интегралом, однако можно построить конечномерный фактормодуль модуля Вермы. Таким образом, модули Верма играют важную роль в классификации конечномерных представлений ${\mathfrak {g}}$ . В частности, они являются важным инструментом в сложной части теоремы о наибольшем весе , а именно показывают, что каждый доминирующий целочисленный элемент фактически возникает как наивысший вес конечномерного неприводимого представления ${\mathfrak {g}}$ .

Теперь мы попытаемся интуитивно понять, что такое модуль Верма с наибольшим весом. $\lambda$ должно выглядеть так. С $v$ должен быть вектором с наибольшим весом с весом $\lambda$ , мы, конечно, хотим

H\cdot v=\lambda (H)v,\quad H\in {\mathfrak {h}}

и

X_{\alpha }\cdot v=0,\quad \alpha \in R^{+}

.

Затем $W_{\lambda }$ должно быть охвачено элементами, полученными понижением $v$ действием $Y_{\alpha }$ х:

Y_{\alpha _{i_{1}}}\cdots Y_{\alpha _{i_{M}}}\cdot v

.

Теперь мы наложим только те отношения между векторами указанного выше вида, которые требуются коммутационными соотношениями между векторами $Y$ х. В частности, модуль Верма всегда бесконечномерен. Вес модуля Verma с наибольшим весом $\lambda$ будет состоять из всех элементов $\mu$ который можно получить из $\lambda$ путем вычитания целых комбинаций положительных корней. На рисунке показан вес модуля Verma для ${\mathfrak {sl}}(3;\mathbb {C} )$ .

Простой аргумент переупорядочения показывает, что существует только один возможный способ, которым полная алгебра Ли ${\mathfrak {g}}$ может действовать в этом пространстве. В частности, если $Z$ это любой элемент ${\mathfrak {g}}$ , то с помощью простой части теоремы Пуанкаре–Биркгофа–Витта мы можем переписать

ZY_{\alpha _{i_{1}}}\cdots Y_{\alpha _{i_{M}}}

как линейная комбинация произведений элементов алгебры Ли с повышающими операторами $X_{\alpha }$ первыми действуют элементы подалгебры Картана, а в последнюю очередь понижающие операторы $Y_{\alpha }$ . Применяя эту сумму слагаемых к $v$ , любой член с повышающим оператором равен нулю, любые множители Картана действуют как скаляры, и, таким образом, мы получаем элемент исходной формы.

Чтобы лучше понять структуру модуля Верма, мы можем выбрать порядок положительных корней следующим образом: $\alpha _{1},\ldots \alpha _{n}$ и соответствующие понижающие операторы обозначим через $Y_{1},\ldots Y_{n}$ . Затем с помощью простого аргумента переупорядочения каждый элемент приведенной выше формы можно переписать как линейную комбинацию элементов с $Y$ в определенном порядке:

Y_{1}^{k_{1}}\cdots Y_{n}^{k_{n}}v

,

где $k_{j}$ 's - неотрицательные целые числа. Собственно, такие векторы и составляют основу модуля Вермы.

Хотя данное описание модуля Verma дает интуитивное представление о том, что $W_{\lambda }$ Похоже, осталось еще дать его строгую конструкцию. В любом случае модуль Верма дает — для любого $\lambda$ , не обязательно доминантное или целочисленное — представление с наибольшим весом $\lambda$ . Цена, которую мы платим за эту относительно простую конструкцию, заключается в том, что $W_{\lambda }$ всегда бесконечномерен. В случае, когда $\lambda$ является доминантным и целым, можно построить конечномерный неприводимый фактор модуля Вермы. ^[3]

Случай sl(2; C) [ править ]

Позволять ${X,Y,H}$ быть обычной основой для $\mathrm {sl} (2;\mathbb {C} )$ :

X={\begin{pmatrix}0&1\\0&0\end{pmatrix}}\qquad Y={\begin{pmatrix}0&0\\1&0\end{pmatrix}}\qquad H={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}~,

при этом подалгебра Картана является промежутком $H$ . Позволять $\lambda$ определяться $\lambda (H)=m$ для произвольного комплексного числа $m$ . Тогда модуль Вермы с наибольшим весом $\lambda$ натянут линейно независимыми векторами $v_{0},v_{1},v_{2},\dots$ а действие базовых элементов заключается в следующем: ^[4]

Y\cdot v_{j}=v_{j+1};\quad X\cdot v_{j}=j(m-(j-1))v_{j-1};\quad H\cdot v_{j}=(m-2j)v_{j}

.

(Это означает, в частности, что $H\cdot v_{0}=mv_{0}$ и это $X\cdot v_{0}=0$ .) Эти формулы мотивированы тем, как базисные элементы действуют в конечномерных представлениях $\mathrm {sl} (2;\mathbb {C} )$ , за исключением того, что мы больше не требуем, чтобы «цепочка» собственных векторов для $H$ должен прекратиться.

В этой конструкции $m$ — произвольное комплексное число, не обязательно вещественное, положительное или целое. Тем не менее, случай, когда $m$ является неотрицательным целым числом, является особенным. В этом случае размах векторов $v_{m+1},v_{m+2},\ldots$ легко видеть, что оно инвариантно, поскольку $X\cdot v_{m+1}=0$ . Тогда фактор-модуль представляет собой конечномерное неприводимое представление $\mathrm {sl} (2;\mathbb {C} )$ размера $m+1.$

Определение модулей Verma [ править ]

Существует две стандартные конструкции модуля Верма, обе из которых включают концепцию универсальной обертывающей алгебры . Продолжим обозначения предыдущего раздела: ${\mathfrak {g}}$ — комплексная полупростая алгебра Ли, ${\mathfrak {h}}$ — фиксированная подалгебра Картана, $R$ — ассоциированная корневая система с фиксированным набором $R^{+}$ положительных корней. Для каждого $\alpha \in R^{+}$ , выбираем ненулевые элементы $X_{\alpha }\in {\mathfrak {g}}_{\alpha }$ и $Y_{\alpha }\in {\mathfrak {g}}_{-\alpha }$ .

Как частное обертывающей алгебры [ править ]

Первое строительство ^[5] модуля Верма является фактором универсальной обертывающей алгебры $U({\mathfrak {g}})$ из ${\mathfrak {g}}$ . Поскольку модуль Verma должен быть ${\mathfrak {g}}$ -модуль, это тоже будет $U({\mathfrak {g}})$ -модуль по универсальному свойству обертывающей алгебры. Таким образом, если у нас есть модуль Верма $W_{\lambda }$ с вектором наибольшего веса $v$ , будет линейная карта $\Phi$ от $U({\mathfrak {g}})$ в $W_{\lambda }$ данный

\Phi (x)=x\cdot v,\quad x\in U({\mathfrak {g}})

.

С $W_{\lambda }$ предполагается, что он генерируется $v$ , карта $\Phi$ должно быть сюръективным. С $v$ Предполагается, что это вектор с наибольшим весом, ядро $\Phi$ должен включать все корневые векторы $X_{\alpha }$ для $\alpha$ в $R^{+}$ . Поскольку также $v$ должен быть весовым вектором с весом $\lambda$ , ядро $\Phi$ должен включать все векторы формы

H-\lambda (H)1,\quad H\in {\mathfrak {h}}

.

Наконец, ядро $\Phi$ должен быть левый идеал в $U({\mathfrak {g}})$ ; в конце концов, если $x\cdot v=0$ затем $(yx)\cdot v=y\cdot (x\cdot v)=0$ для всех $y\in U({\mathfrak {g}})$ .

Предыдущее обсуждение мотивирует следующую конструкцию модуля Вермы. Мы определяем $W_{\lambda }$ как фактор-векторное пространство

W_{\lambda }=U({\mathfrak {g}})/I_{\lambda }

,

где $I_{\lambda }$ — левый идеал, порожденный всеми элементами формы

X_{\alpha },\quad \alpha \in R^{+},

и

H-\lambda (H)1,\quad H\in {\mathfrak {h}}

.

Потому что $I_{\lambda }$ — левый идеал, естественное левое действие $U({\mathfrak {g}})$ на себе переходит в частное. Таким образом, $W_{\lambda }$ это $U({\mathfrak {g}})$ -модуль и, следовательно, также ${\mathfrak {g}}$ -модуль.

Расширением скаляров [ править ]

Процедура « расширения скаляров » — это метод замены левого модуля. $V$ над одной алгеброй $A_{1}$ (не обязательно коммутативный) в левый модуль над большей алгеброй $A_{2}$ который содержит $A_{1}$ как подалгебра. Мы можем подумать о $A_{2}$ как право $A_{1}$ -модуль, где $A_{1}$ действует на $A_{2}$ умножением справа. С $V$ это левый $A_{1}$ -модуль и $A_{2}$ это право $A_{1}$ -модуля, мы можем сформировать тензорное произведение этих двух над алгеброй $A_{1}$ :

A_{2}\otimes _{A_{1}}V

.

Теперь, поскольку $A_{2}$ это левый $A_{2}$ -модуля над собой, вышеуказанное тензорное произведение несет структуру левого модуля над большей алгеброй $A_{2}$ , однозначно определяемое требованием, чтобы

a_{1}\cdot (a_{2}\otimes v)=(a_{1}a_{2})\otimes v

для всех $a_{1}$ и $a_{2}$ в $A_{2}$ . Таким образом, начиная слева $A_{1}$ -модуль $V$ , мы создали левую $A_{2}$ -модуль $A_{2}\otimes _{A_{1}}V$ .

Теперь мы применим эту конструкцию в случае полупростой алгебры Ли. Мы позволяем ${\mathfrak {b}}$ быть подалгеброй ${\mathfrak {g}}$ охватываемый ${\mathfrak {h}}$ и корневые векторы $X_{\alpha }$ с $\alpha \in R^{+}$ . (Таким образом, ${\mathfrak {b}}$ является «борелевской подалгеброй» ${\mathfrak {g}}$ .) Можем сформировать левый модуль $F_{\lambda }$ над универсальной обертывающей алгеброй $U({\mathfrak {b}})$ следующее:

$F_{\lambda }$ - это одномерное векторное пространство, натянутое одним вектором $v$ вместе с ${\mathfrak {b}}$ - модуля такая, что структура ${\mathfrak {h}}$ действует как умножение на $\lambda$ и пространства положительных корней действуют тривиально:

\quad H\cdot v=\lambda (H)v,\quad H\in {\mathfrak {h}};\quad X_{\alpha }\cdot v=0,\quad \alpha \in R^{+}

.

Смысл этой формулы в том, что она описывает, как $U({\mathfrak {b}})$ предполагается, что он действует на вектор с наибольшим весом в модуле Verma.

следует, Теперь из теоремы Пуанкаре–Биркгофа–Витта что $U({\mathfrak {b}})$ является подалгеброй $U({\mathfrak {g}})$ . Таким образом, мы можем применить расширение скалярной техники для преобразования $F_{\lambda }$ слева $U({\mathfrak {b}})$ -модуль влево $U({\mathfrak {g}})$ -модуль $W_{\lambda }$ следующим образом:

W_{\lambda }:=U({\mathfrak {g}})\otimes _{U({\mathfrak {b}})}F_{\lambda }

.

С $W_{\lambda }$ это левый $U({\mathfrak {g}})$ -модуль, это, в частности, модуль (представление) для ${\mathfrak {g}}$ .

Структура модуля Verma [ править ]

Какая бы конструкция модуля Верма ни использовалась, необходимо доказать, что она нетривиальна, т. е. не является нулевым модулем. На самом деле можно использовать теорему Пуанкаре–Биркгофа–Витта, чтобы показать, что лежащее в основе векторное пространство $W_{\lambda }$ изоморфен

U({\mathfrak {g}}_{-})

где ${\mathfrak {g}}_{-}$ — подалгебра Ли, порожденная пространствами отрицательных корней ${\mathfrak {g}}$ (то есть, $Y_{\alpha }$ х). ^[6]

Основные свойства [ править ]

Модули Верма, рассматриваемые как ${\mathfrak {g}}$ -модули с наибольшим являются модулями с наибольшим весом , т.е. они генерируются вектором весом . Этот вектор с наибольшим весом $1\otimes 1$ (первый $1$ это единица в ${\mathcal {U}}({\mathfrak {g}})$ и второйотряд в поле $F$ , рассматриваемый как ${\mathfrak {b}}$ - модуль $F_{\lambda }$ ) и имеет вес $\lambda$ .

Множественность [ править ]

Модули Верма являются весовыми модулями , т.е. $W_{\lambda }$ является прямой суммой всех своих весовых пространств . Каждое весовое место в $W_{\lambda }$ конечномерен, а размерность $\mu$ - весовое пространство $W_{\mu }$ это количество способов выражения $\lambda -\mu$ как сумма положительных корней (это тесно связано с так называемой статистической суммой Костанта ). Это утверждение следует из предыдущего утверждения о том, что модуль Верма изоморфен как векторное пространство $U({\mathfrak {g}}_{-})$ , а также теорему Пуанкаре–Биркгофа–Витта для $U({\mathfrak {g}}_{-})$ .

Универсальная собственность [ править ]

Модули Verma обладают очень важным свойством: если $V$ любое представление, порожденное вектором с наибольшим весом веса $\lambda$ , есть сюръектив ${\mathfrak {g}}$ - гомоморфизм $W_{\lambda }\to V.$ То есть все представления с наибольшим весом $\lambda$ которые генерируются вектором с наибольшим весом (так называемые модули с наибольшим весом , являются частными ) $W_{\lambda }.$

Неприводимый модуль частного [ править ]

$W_{\lambda }$ содержит единственный максимальный подмодуль , а его фактор является единственным (с точностью до изоморфизма ) неприводимым представлением со старшим весом $\lambda .$ ^[7] Если наибольший вес $\lambda$ является доминантным и целым, то затем доказывается, что этот неприводимый фактор на самом деле конечномерен. ^[8]

В качестве примера рассмотрим случай ${\mathfrak {g}}=\operatorname {sl} (2;\mathbb {C} )$ обсуждалось выше. Если наибольший вес $m$ является «доминирующим целым» — это просто означает, что это неотрицательное целое число — тогда $Xv_{m+1}=0$ и размах элементов $v_{m+1},v_{m+2},\ldots$ является инвариантным. Тогда факторпредставление неприводимо с размерностью $m+1$ . Факторпредставление натянуто на линейно независимые векторы $v_{0},v_{1},\ldots ,v_{m}$ . Действие $\operatorname {sl} (2;\mathbb {C} )$ то же самое, что и в модуле Verma, за исключением того, что $Yv_{m}=0$ в частном, по сравнению с $Yv_{m}=v_{m+1}$ в модуле Верма.

Модуль Верма $W_{\lambda }$ сам по себе неприводим тогда и только тогда, когда $\lambda$ является антидоминантным. ^[9] Следовательно, когда $\lambda$ является целостным, $W_{\lambda }$ неприводима тогда и только тогда, когда ни одна из координат $\lambda$ в базисе фундаментальных весов находится из множества $\{0,1,2,\ldots \}$ , хотя в общем случае это условие необходимо, но недостаточно для $W_{\lambda }$ быть нередуцируемым.

Другая недвижимость [ править ]

Модуль Верма $W_{\lambda }$ называется регулярным , если его старший вес λ находится на аффинной орбите Вейля доминантного веса ${\tilde {\lambda }}$ . Другими словами, существует элемент w группы Вейля W такой, что

\lambda =w\cdot {\tilde {\lambda }}

где $\cdot$ — аффинное действие группы Вейля .

Модуль Верма $W_{\lambda }$ называется сингулярным , если на аффинной орбите λ нет доминирующего веса. В этом случае существует вес ${\tilde {\lambda }}$ так что ${\tilde {\lambda }}+\delta$ находится на стенке фундаментальной камеры Вейля (δ — сумма всех фундаментальных весов ).

Гомоморфизмы модулей Вермы [ править ]

Для любых двух весов $\lambda ,\mu$ нетривиальный гомоморфизм

W_{\mu }\rightarrow W_{\lambda }

может существовать только в том случае, если $\mu$ и $\lambda$ связаны с аффинным действием группы Вейля $W$ алгебры Ли ${\mathfrak {g}}$ . Это легко следует из теоремы Хариш-Чандры о бесконечно малых центральных характерах .

Каждый гомоморфизм модулей Верма инъективен и размерность

\dim(\operatorname {Hom} (W_{\mu },W_{\lambda }))\leq 1

для любого $\mu ,\lambda$ . Итак, существует ненулевое $W_{\mu }\rightarrow W_{\lambda }$ тогда и только тогда, когда $W_{\mu }$ изоморфен (единственному ) подмодулю модуля $W_{\lambda }$ .

Полную классификацию гомоморфизмов модулей Вермы выполнил Бернштейн – Гельфанд – Гельфанд. ^[10] и Верма ^[11] и можно резюмировать в следующем утверждении:

Существует ненулевой гомоморфизм $W_{\mu }\rightarrow W_{\lambda }$ тогда и только тогда, когда существует
последовательность весов
$\mu =\nu _{0}\leq \nu _{1}\leq \ldots \leq \nu _{k}=\lambda$
такой, что $\nu _{i-1}+\delta =s_{\gamma _{i}}(\nu _{i}+\delta )$ для некоторых положительных корней $\gamma _{i}$ (и $s_{\gamma _{i}}$ – соответствующее корневое отражение и $\delta$ представляет собой сумму всех фундаментальных весов ) и для каждого $1\leq i\leq k,(\nu _{i}+\delta )(H_{\gamma _{i}})$ это натуральное число ( $H_{\gamma _{i}}$ это корень, связанный с корнем $\gamma _{i}$ ).

Если модули Verma $M_{\mu }$ и $M_{\lambda }$ регулярны , то существует единственный доминирующий вес ${\tilde {\lambda }}$ и единственные элементы w , w ′ группы Вейля W такие, что

\mu =w'\cdot {\tilde {\lambda }}

и

\lambda =w\cdot {\tilde {\lambda }},

где $\cdot$ — аффинное действие группы Вейля. Если веса далее целые , то существует ненулевой гомоморфизм

W_{\mu }\to W_{\lambda }

тогда и только тогда, когда

w\leq w'

в порядке Брюа группы Вейля.

Джордана Серия – Гельдера

Позволять

0\subset A\subset B\subset W_{\lambda }

быть последовательностью ${\mathfrak {g}}$ -модулей так, что фактор B/A неприводим со старшим весом µ. Тогда существует ненулевой гомоморфизм $W_{\mu }\to W_{\lambda }$ .

Легким следствием этого является то, что для любых модулей с наибольшим весом $V_{\mu },V_{\lambda }$ такой, что

V_{\mu }\subset V_{\lambda }

существует ненулевой гомоморфизм $W_{\mu }\to W_{\lambda }$ .

Резолюция Бернштейна–Гельфанда–Гельфанда [ править ]

Позволять $V_{\lambda }$ — конечномерное неприводимое представление алгебры Ли ${\mathfrak {g}}$ с наибольшим весом λ. Из раздела о гомоморфизмах модулей Вермы мы знаем, что существует гомоморфизм

W_{w'\cdot \lambda }\to W_{w\cdot \lambda }

тогда и только тогда, когда

w\leq w'

в порядке Брюа группы Вейля . Следующая теорема описывает разрешение проективное $V_{\lambda }$ в терминах модулей Верма (доказано Бернштейном – Гельфандом – Гельфандом в 1975 г.) ^[12]) :

Существует точная последовательность ${\mathfrak {g}}$ -гомоморфизмы
$0\to \oplus _{w\in W,\,\,\ell (w)=n}W_{w\cdot \lambda }\to \cdots \to \oplus _{w\in W,\,\,\ell (w)=2}W_{w\cdot \lambda }\to \oplus _{w\in W,\,\,\ell (w)=1}W_{w\cdot \lambda }\to W_{\lambda }\to V_{\lambda }\to 0$
где n — длина наибольшего элемента группы Вейля.

Аналогичное решение существует для обобщенных модулей Вермы и . Кратко это обозначается как резолюция BGG .

См. также [ править ]

Примечания [ править ]

^ Например, Холл 2015, глава 9.
^ Зал 2015 г., раздел 9.2.
^ Зал 2015 г., разделы 9.6 и 9.7.
^ Зал 2015 г., разделы 9.2.
^ Зал 2015 г., раздел 9.5.
^ Холл, 2015 г., Теорема 9.14.
^ Зал 2015 г., раздел 9.6.
^ Зал 2015 г., раздел 9.7.
^ Хамфрис, Джеймс (22 июля 2008 г.). Представления полупростых алгебр Ли в категории BGG 𝒪 . Аспирантура по математике. Том. 94. Американское математическое общество. дои : 10.1090/gsm/094 . ISBN 978-0-8218-4678-0 .
^ Бернштейн И.Н., Гельфанд И.М., Гельфанд С.И., Структура представлений, порожденных векторами старшего веса, Функционал. Анальный. Прил. 5 (1971)
^ Верма Н., Структура некоторых индуцированных представлений комплексных полупростых алгебр Ли, Bull. амер. Математика. Соц. 74 (1968)
^ Бернштейн И.Н., Гельфанд И.М., Гельфанд С.И., Дифференциальные операторы в базовом аффинном пространстве и исследование g-модулей, групп Ли и их представлений , И.М. Гельфанд, Ред., Адам Хильгер, Лондон, 1975.

Ссылки [ править ]

Бауэрле, GGA; де Керф, Э.А.; тен Кроуд, APE (1997). А. ван Грозен; Э.М. де Ягер (ред.). Конечно- и бесконечномерные алгебры Ли и их применение в физике . Исследования по математической физике. Том. 7. Северная Голландия. Глава 20. ISBN 978-0-444-82836-1 – через ScienceDirect .
Картер, Р. (2005), Алгебры Ли конечного и аффинного типа , Cambridge University Press, ISBN 978-0-521-85138-1 .
Диксмье, Дж. (1977), Обертывающие алгебры , Амстердам, Нью-Йорк, Оксфорд: Северная Голландия, ISBN 978-0-444-11077-0 .
Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для аспирантов по математике, том. 222 (2-е изд.), Спрингер, ISBN 978-3319134666
Хамфрис, Дж. (1980), Введение в алгебры Ли и теорию представлений , Springer Verlag, ISBN 978-3-540-90052-8 .
Кнапп, AW (2002), Группы лжи за пределами введения (2-е изд.), Birkhäuser, стр. 285, ISBN 978-0-8176-3926-6 .
Роча, Альвани (2001) [1994], «Разрешение BGG» , Энциклопедия математики , EMS Press
Роггенкамп, К.; Стефанеску, М. (2002), Алгебра — теория представлений , Springer, ISBN 978-0-7923-7114-4 .

В эту статью включены материалы из модуля Verma на PlanetMath , который распространяется по лицензии Creative Commons Attribution/Share-Alike License .

[1] Например, Холл 2015, глава 9.

[2] Зал 2015 г., раздел 9.2.

[3] Зал 2015 г., разделы 9.6 и 9.7.

[4] Зал 2015 г., разделы 9.2.

[5] Зал 2015 г., раздел 9.5.

[6] Холл, 2015 г., Теорема 9.14.

[7] Зал 2015 г., раздел 9.6.

[8] Зал 2015 г., раздел 9.7.

[9] Хамфрис, Джеймс (22 июля 2008 г.). Представления полупростых алгебр Ли в категории BGG 𝒪 . Аспирантура по математике. Том. 94. Американское математическое общество. дои : 10.1090/gsm/094 . ISBN 978-0-8218-4678-0 .

[10] Бернштейн И.Н., Гельфанд И.М., Гельфанд С.И., Структура представлений, порожденных векторами старшего веса, Функционал. Анальный. Прил. 5 (1971)

[11] Верма Н., Структура некоторых индуцированных представлений комплексных полупростых алгебр Ли, Bull. амер. Математика. Соц. 74 (1968)

[12] Бернштейн И.Н., Гельфанд И.М., Гельфанд С.И., Дифференциальные операторы в базовом аффинном пространстве и исследование g-модулей, групп Ли и их представлений , И.М. Гельфанд, Ред., Адам Хильгер, Лондон, 1975.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]