Корневая система

Эта статья о корневых системах в математике. О растений корневых системах см. Корень .

В математике корневая система — это конфигурация векторов в евклидовом пространстве, удовлетворяющая определённым геометрическим свойствам. Это понятие является фундаментальным в теории групп Ли и алгебр Ли , особенно в теории классификации и представлений полупростых алгебр Ли . Поскольку группы Ли (и некоторые аналоги, такие как алгебраические группы ) и алгебры Ли стали важными во многих областях математики в течение двадцатого века, кажущаяся особая природа корневых систем скрывает количество областей, в которых они применяются. Кроме того, схема классификации корневых систем с помощью диаграмм Дынкина встречается в разделах математики, не имеющих явной связи с теорией Ли (например, в теории особенностей ). Наконец, корневые системы важны сами по себе, как и в теории спектральных графов .

Определения и примеры

Шесть векторов корневой системы A ₂

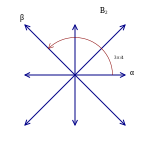
примера рассмотрим шесть векторов в двумерном евклидовом пространстве R В качестве первого ² , как показано на изображении справа; назовите их корнями . Эти векторы охватывают все пространство. Если рассматривать линию, перпендикулярную любому корню, скажем β , то отражение R ² в этой строке отправляет любой другой корень, скажем α , в другой корень. При этом корень, которому оно отправляется, равен α + nβ , где n — целое число (в данном случае n равно 1). Эти шесть векторов удовлетворяют следующему определению и, следовательно, образуют корневую систему; этот известен как A ₂ .

Определение

Пусть E — конечномерное евклидово векторное пространство со стандартным евклидовым скалярным произведением , обозначаемым $(\cdot ,\cdot )$. Корневая система $\Phi$ в E — это конечное множество ненулевых векторов (называемых корнями ), которые удовлетворяют следующим условиям:

1. Корни простираются Е. на
2. Единственные скалярные кратные корня $\alpha \in \Phi$ которые принадлежат $\Phi$ являются $\alpha$ себя и $-\alpha$.
3. Для каждого корня $\alpha \in \Phi$, набор $\Phi$ замкнут при отражении через гиперплоскость, перпендикулярную $\alpha$.
4. ( Целостность ) Если $\alpha$ и $\beta$ корни в $\Phi$, то проекция $\beta$ на линию через $\alpha$ является целым числом или полуцелым кратным $\alpha$.

Эквивалентный способ записи условий 3 и 4 следующий:

3. Для любых двух корней $\alpha ,\beta \in \Phi$, набор $\Phi$ содержит элемент $\sigma _{\alpha }(\beta ):=\beta -2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\alpha .$
4. Для любых двух корней $\alpha ,\beta \in \Phi$, число $\langle \beta ,\alpha \rangle :=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}$ является целым числом .

Некоторые авторы включают в определение корневой системы только условия 1–3. В этом контексте корневая система, которая также удовлетворяет условию целостности, известна как кристаллографическая корневая система . Другие авторы опускают условие 2; тогда корневые системы, удовлетворяющие условию 2, называют редуцированными . В данной статье все корневые системы предполагаются редуцированными и кристаллографическими.

Ввиду свойства 3 условие целочисленности эквивалентно утверждению, что β и его отражение σ _α ( β ) отличаются на целое число, кратное α . Обратите внимание, что оператор $$\langle \cdot ,\cdot \rangle \colon \Phi \times \Phi \to \mathbb {Z}$$ определяемый свойством 4, не является внутренним продуктом. Оно не обязательно симметрично и линейно только по первому аргументу.

Корневые системы ранга 2

Корневая система $A_{1}\times A_{1}$	Корневая система $D_{2}$
Корневая система $A_{2}$	Корневая система $G_{2}$
Корневая система $B_{2}$	Корневая система $C_{2}$

Ранг корневой системы это размерность E. Φ — Две корневые системы можно объединить, рассматривая евклидовы пространства, которые они охватывают, как взаимно ортогональные подпространства общего евклидова пространства. , например системы A2 _, , B2 _{Корневая система ,} и G2 _{которая не возникает в результате такой комбинации} изображенные справа, называется неприводимой .

системы корней ( E1 _если , Φ1 ₎ и ( E2 _→ , Φ2 ₎ называются изоморфными, существует обратимое линейное преобразование Две _E1 E2 , _{переводящее} Φ1 _в Φ2 _такое , что для каждой пары корней число $\langle x,y\rangle$ сохраняется.

The корневая решетка системы корней Φ — это Z -подмодуль модуля E, порожденный Φ. Это решетка в E .

Группа Вейля

Основная статья: Группа Вейля

Группа Вейля $A_{2}$ корневая система - группа симметрии равностороннего треугольника

Группа группой изометрий , E порожденная отражениями через гиперплоскости , связанные с корнями Φ, называется Вейля Φ. Поскольку группа Вейля действует точно на конечном множестве Φ, она всегда конечна. Плоскости отражения — это гиперплоскости, перпендикулярные корням, обозначенные для $A_{2}$ пунктирными линиями на рисунке ниже. Группа Вейля — это группа симметрии равностороннего треугольника, состоящего из шести элементов. В этом случае группа Вейля не является полной группой симметрии корневой системы (например, поворот на 60 градусов является симметрией корневой системы, но не является элементом группы Вейля).

Оцените один пример

Существует только одна корневая система ранга 1, состоящая из двух ненулевых векторов. $\{\alpha ,-\alpha \}$. Эта корневая система называется $A_{1}$.

Расположите два примера

В ранге 2 имеются четыре возможности, соответствующие $\sigma _{\alpha }(\beta )=\beta +n\alpha$, где $n=0,1,2,3$. На рисунке справа показаны эти возможности, но с некоторыми дублированиями: $A_{1}\times A_{1}$ изоморфен $D_{2}$ и $B_{2}$ изоморфен $C_{2}$.

Обратите внимание, что корневая система не определяется решеткой, которую она порождает: $A_{1}\times A_{1}$ и $B_{2}$ оба создают квадратную решетку, а $A_{2}$ и $G_{2}$ оба порождают шестиугольную решетку .

Если Φ — система корней в E , а S — подпространство в E, на Ψ = Φ ∩ S , то Ψ — система корней в S. натянутое Таким образом, исчерпывающий список четырех корневых систем ранга 2 показывает геометрические возможности любых двух корней, выбранных из корневой системы произвольного ранга. В частности, два таких корня должны встретиться под углом 0, 30, 45, 60, 90, 120, 135, 150 или 180 градусов.

Системы корней, возникающие из полупростых алгебр Ли

См. также: Полупростая алгебра Ли § Подалгебры Картана и системы корней и Система корней полупростой алгебры Ли.

Если ${\mathfrak {g}}$ — комплексная полупростая алгебра Ли и ${\mathfrak {h}}$ является подалгеброй Картана , мы можем построить систему корней следующим образом. Мы говорим, что $\alpha \in {\mathfrak {h}}^{*}$ является корнем ​ ${\mathfrak {g}}$ относительно ${\mathfrak {h}}$ если $\alpha \neq 0$ и существует некоторый $X\neq 0\in {\mathfrak {g}}$ такой, что $$[H,X]=\alpha (H)X$$ для всех $H\in {\mathfrak {h}}$. Можно показать что существует внутренний продукт, для которого набор корней образует корневую систему. Корневая система ${\mathfrak {g}}$ является основным инструментом анализа структуры ${\mathfrak {g}}$ и классифицировать его представления. (См. раздел ниже, посвященный системам корней и теории Ли.)

История

Понятие корневой системы было первоначально введено Вильгельмом Киллингом примерно в 1889 году (на немецком языке Wurzelsystem ). Он использовал их в своей попытке классифицировать все простые алгебры Ли над полем комплексных чисел . Киллинг первоначально допустил ошибку в классификации, перечислив две исключительные корневые системы 4-го ранга, хотя на самом деле существует только одна, теперь известная как F ₄ . Позже Картан исправил эту ошибку, показав, что две корневые системы Киллинга изоморфны.

Киллинг исследовал структуру алгебры Ли. $L$, рассматривая то, что сейчас называется подалгеброй Картана ${\mathfrak {h}}$. Затем он изучил корни характеристического многочлена $\det(\operatorname {ad} _{L}x-t)$, где $x\in {\mathfrak {h}}$. Здесь корень рассматривается как функция ${\mathfrak {h}}$, или даже как элемент двойственного векторного пространства ${\mathfrak {h}}^{*}$. Этот набор корней образует корневую систему внутри ${\mathfrak {h}}^{*}$, как определено выше, где внутренний продукт представляет собой форму Киллинга .

Элементарные следствия аксиом корневой системы

Условие целочисленности $\langle \beta ,\alpha \rangle$ выполняется только для β на одной из вертикальных прямых, а условие целости для $\langle \alpha ,\beta \rangle$ выполняется только для β на одном из красных кружков. Любой β, перпендикулярный α (на оси Y ), тривиально удовлетворяет обоим значениям 0, но не определяет неприводимую систему корней.
По модулю отражения для данного α существует только 5 нетривиальных возможностей для β и 3 возможных угла между α и β в наборе простых корней. Буквы в нижнем индексе соответствуют ряду корневых систем, для которых данное β может служить первым корнем, а α — вторым корнем (или в F ₄ — средними 2 корнями).

Косинус угла между двумя корнями ограничивается половиной квадратного корня из положительного целого числа. Это потому, что $\langle \beta ,\alpha \rangle$ и $\langle \alpha ,\beta \rangle$ оба являются целыми числами, по предположению, и $${\begin{aligned}\langle \beta ,\alpha \rangle \langle \alpha ,\beta \rangle &=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\cdot 2{\frac {(\alpha ,\beta )}{(\beta ,\beta )}}\\&=4{\frac {(\alpha ,\beta )^{2}}{\vert \alpha \vert ^{2}\vert \beta \vert ^{2}}}\\&=4\cos ^{2}(\theta )=(2\cos(\theta ))^{2}\in \mathbb {Z} .\end{aligned}}$$

С $2\cos(\theta )\in [-2,2]$, единственно возможные значения для $\cos(\theta )$ являются $0,\pm {\tfrac {1}{2}},\pm {\tfrac {\sqrt {2}}{2}},\pm {\tfrac {\sqrt {3}}{2}}$ и $\pm {\tfrac {\sqrt {4}}{2}}=\pm 1$, что соответствует углам 90°, 60° или 120°, 45° или 135°, 30° или 150° и 0° или 180°. Условие 2 гласит, что никакие скалярные числа α, кроме 1 и −1, не могут быть корнями, поэтому 0 или 180 °, которые соответствовали бы 2 α или −2 α , отсутствуют. На диаграмме справа показано, что угол 60° или 120° соответствует корням одинаковой длины, а угол 45° или 135° соответствует соотношению длин ${\sqrt {2}}$ а угол 30° или 150° соответствует соотношению длин ${\sqrt {3}}$.

Таким образом, вот единственные возможности для каждой пары корней.

• Угол 90 градусов; в этом случае соотношение длин не ограничено.
• Угол 60 или 120 градусов, с коэффициентом длины 1.
• Угол 45 или 135 градусов, с соотношением длин ${\sqrt {2}}$.
• Угол 30 или 150 градусов, с соотношением длин ${\sqrt {3}}$.

Положительные корни и простые корни

Помеченные корни представляют собой набор положительных корней для $G_{2}$ корневая система, с $\alpha _{1}$ и $\alpha _{2}$ это простые корни

Имея корневую систему $\Phi$ мы всегда можем выбрать (разными способами) набор положительных корней . Это подмножество $\Phi ^{+}$ из $\Phi$ такой, что

• Для каждого корня $\alpha \in \Phi$ ровно один из корней $\alpha$, $-\alpha$ содержится в $\Phi ^{+}$.
• Для любых двух различных $\alpha ,\beta \in \Phi ^{+}$ такой, что $\alpha +\beta$ это корень, $\alpha +\beta \in \Phi ^{+}$.

Если множество положительных корней $\Phi ^{+}$ выбраны элементы $-\Phi ^{+}$ называются отрицательными корнями . Набор положительных корней можно построить, выбрав гиперплоскость $V$ не содержащий никакого корня и настроек $\Phi ^{+}$ чтобы все корни лежали на фиксированной стороне $V$. Более того, таким образом возникает любое множество положительных корней.

Элемент $\Phi ^{+}$ называется простым корнем (также фундаментальным корнем ), если его нельзя записать в виде суммы двух элементов $\Phi ^{+}$. (Набор простых корней также называют базой для $\Phi$.) Набор $\Delta$ простых корней является основой $E$ со следующими дополнительными специальными свойствами:

• Каждый корень $\alpha \in \Phi$ представляет собой линейную комбинацию элементов $\Delta$ с целыми коэффициентами.
• Для каждого $\alpha \in \Phi$, коэффициенты в предыдущем пункте либо все неотрицательные, либо все неположительные.

Для каждой корневой системы $\Phi$ существует много различных вариантов выбора набора положительных корней - или, что то же самое, простых корней - но любые два набора положительных корней различаются действием группы Вейля.

Двойная корневая система, корни и цельные элементы

Смотрите также: двойная группа Ленглендса

Двойная корневая система

Если Φ — система корней в E , то корень α ^∨ корня α определяется формулой $$\alpha ^{\vee }={2 \over (\alpha ,\alpha )}\,\alpha .$$

Множество кокорней также образует корневую систему Φ ^∨ в E , называемой двойной корневой системой (или иногда обратной корневой системой ). По определению, α ^{∨ ∨} = α, так что Φ — двойственная система корней к Φ ^∨ . Решетка в E, натянутая на Φ ^∨ называется решеткой кокорней . И Φ, и Φ ^∨ имеют одну и ту же группу Вейля W и для s из W , $$(s\alpha )^{\vee }=s(\alpha ^{\vee }).$$

Если ∆ — множество простых корней для Φ, то ∆ ^∨ есть набор простых корней для Φ ^∨ .

В описанной ниже классификации корневые системы типа $A_{n}$ и $D_{n}$ наряду с исключительной корневой системой $E_{6},E_{7},E_{8},F_{4},G_{2}$ все самодвойственны, что означает, что двойственная корневая система изоморфна исходной корневой системе. Напротив, $B_{n}$ и $C_{n}$ корневые системы двойственны друг другу, но не изоморфны (за исключением случаев, когда $n=2$).

Неотъемлемые элементы

См. также: Вес (теория представлений) § Веса в теории представлений полупростых алгебр Ли.

Вектор $\lambda$ в E называется интегралом если его внутренний продукт с каждым кокорнем является целым числом: $$2{\frac {(\lambda ,\alpha )}{(\alpha ,\alpha )}}\in \mathbb {Z} ,\quad \alpha \in \Phi .$$ Поскольку набор $\alpha ^{\vee }$ с $\alpha \in \Delta$ формирует основу для двойной корневой системы, чтобы убедиться, что $\lambda$ является целым, то достаточно проверить приведенное выше условие для $\alpha \in \Delta$.

Множество целых элементов называется решеткой весов, ассоциированной с данной корневой системой. Этот термин происходит из теории представлений полупростых алгебр Ли , где целые элементы образуют возможные веса конечномерных представлений.

Определение корневой системы гарантирует, что сами корни являются целостными элементами. Таким образом, всякая целочисленная линейная комбинация корней также является целой. Однако в большинстве случаев будут целые элементы, которые не являются целочисленными комбинациями корней. То есть в общем случае решетка весов не совпадает с решеткой корней.

Классификация корневых систем по диаграммам Дынкина

См. Также: Диаграмма Дынкина.

Изображения всех связанных диаграмм Дынкина

Корневая система неприводима, если ее нельзя разбить на объединение двух собственных подмножеств. $\Phi =\Phi _{1}\cup \Phi _{2}$, такой, что $(\alpha ,\beta )=0$ для всех $\alpha \in \Phi _{1}$ и $\beta \in \Phi _{2}$ .

Неприводимым корневым системам соответствуют определенные графы — диаграммы Дынкина имени Евгения Дынкина . Классификация этих графов является простым вопросом комбинаторики и приводит к классификации неприводимых корневых систем.

Построение диаграммы Дынкина

Учитывая систему корней, выберите набор простых корней Δ , как в предыдущем разделе. Вершины соответствующей диаграммы Дынкина соответствуют корням из Δ. Ребра между вершинами рисуются следующим образом, в соответствии с углами. (Обратите внимание, что угол между простыми корнями всегда не менее 90 градусов.)

• Нет края, если векторы ортогональны,
• Ненаправленное одиночное ребро, если они составляют угол 120 градусов,
• Направленное двойное ребро, если они составляют угол 135 градусов, а
• Направленное тройное ребро, если они составляют угол 150 градусов.

Термин «направленное ребро» означает, что двойные и тройные ребра отмечены стрелкой, указывающей в сторону более короткого вектора. (Представление о стрелке как о знаке «больше» проясняет, в какую сторону должна указывать стрелка.)

Заметим, что исходя из отмеченных выше элементарных свойств корней, правила построения диаграммы Дынкина можно описать и следующим образом. Нет ребра, если корни ортогональны; для неортогональных корней - одинарное, двойное или тройное ребро в зависимости от того, равно ли отношение длин более длинного к более короткому 1, ${\sqrt {2}}$, ${\sqrt {3}}$. В случае $G_{2}$ корневая система, например, имеется два простых корня под углом 150 градусов (с соотношением длин ${\sqrt {3}}$). Таким образом, диаграмма Дынкина имеет две вершины, соединенные тройным ребром, со стрелкой, указывающей от вершины, связанной с более длинным корнем, к другой вершине. (В этом случае стрелка немного избыточна, поскольку диаграмма эквивалентна независимо от направления стрелки.)

Классификация корневых систем

Хотя данная корневая система имеет более одного возможного набора простых корней, группа Вейля действует транзитивно при таком выборе. Следовательно, диаграмма Дынкина не зависит от выбора простых корней; это определяется самой корневой системой. И наоборот, имея две корневые системы с одинаковой диаграммой Дынкина, можно сопоставить корни, начиная с корней в основании, и показать, что эти системы на самом деле одинаковы.

Таким образом, проблема классификации корневых систем сводится к проблеме классификации возможных диаграмм Дынкина. Корневая система неприводима тогда и только тогда, когда ее диаграммы Дынкина связны. Возможные схемы подключения указаны на рисунке. Нижние индексы указывают количество вершин диаграммы (а значит, и ранг соответствующей неприводимой корневой системы).

Если $\Phi$ — корневая система, диаграмма Дынкина для двойной корневой системы $\Phi ^{\vee }$ получается из диаграммы Дынкина $\Phi$ сохраняя все те же вершины и ребра, но меняя направления всех стрелок на противоположные. Таким образом, из их диаграмм Дынкина мы видим, что $B_{n}$ и $C_{n}$ двойственны друг другу.

Вейль Чемберс и группа Вейля

Смотрите также: группа Кокстера § Аффинные группы Кокстера

Заштрихованная область представляет собой основную камеру Вейля для основания. $\{\alpha _{1},\alpha _{2}\}$

Если $\Phi \subset E$ является корневой системой, мы можем рассматривать гиперплоскость, перпендикулярную каждому корню $\alpha$. Напомним, что $\sigma _{\alpha }$ обозначает отражение относительно гиперплоскости и что группа Вейля — это группа преобразований $E$ созданный всеми $\sigma _{\alpha }$х. Дополнение множества гиперплоскостей несвязно, и каждая компонента связности называется камерой Вейля . Если мы зафиксировали определенный набор простых корней Δ, мы можем определить фундаментальную камеру Вейля, связанную с Δ, как набор точек $v\in E$ такой, что $(\alpha ,v)>0$ для всех $\alpha \in \Delta$.

Поскольку размышления $\sigma _{\alpha },\,\alpha \in \Phi$ сохранять $\Phi$, они также сохраняют множество гиперплоскостей, перпендикулярных корням. Таким образом, каждый элемент группы Вейля переставляет местами камеры Вейля.

На рисунке показан случай $A_{2}$ корневая система. «Гиперплоскости» (в данном случае одномерные), ортогональные корням, обозначены пунктирными линиями. Шесть секторов по 60 градусов — это камеры Вейля, а заштрихованная область — это основная камера Вейля, связанная с указанным основанием.

Основная общая теорема о камерах Вейля такова:

Теорема : Группа Вейля действует свободно и транзитивно в камерах Вейля. Таким образом, порядок группы Вейля равен числу камер Вейля.

В $A_{2}$ Например, группа Вейля состоит из шести элементов и шести камер Вейля.

Связанный результат:

Теорема : Зафиксируйте камеру Вейля. $C$. Тогда для всех $v\in E$, орбита Вейля $v$ содержит ровно одну точку замыкания ${\bar {C}}$ из $C$.

Корневые системы и теория Ли

Неприводимые корневые системы классифицируют ряд связанных объектов теории Ли, в частности следующие:

• простые комплексные алгебры Ли (см. обсуждение систем корней, возникающих из полупростых алгебр Ли выше),
• односвязные комплексные группы Ли, которые являются простыми по модулю центрами, и
• односвязные компактные группы Ли , являющиеся простыми по модулю центрами.

В каждом случае корни — это ненулевые веса присоединенного представления .

Теперь мы дадим краткое указание на то, как неприводимые системы корней классифицируют простые алгебры Ли над $\mathbb {C}$, следуя аргументам Хамфриса. Предварительный результат гласит, что полупростая алгебра Ли является простой тогда и только тогда, когда соответствующая система корней неприводима. Поэтому мы ограничим внимание неприводимыми системами корней и простыми алгебрами Ли.

• Прежде всего, мы должны установить, что для каждой простой алгебры ${\mathfrak {g}}$ имеется только одна корневая система. Это утверждение следует из того, что подалгебра Картана в ${\mathfrak {g}}$ единственна с точностью до автоморфизма, откуда следует, что любые две подалгебры Картана дают изоморфные корневые системы.
• Далее нам нужно показать, что для каждой неприводимой системы корней может существовать не более одной алгебры Ли, т. е. что система корней определяет алгебру Ли с точностью до изоморфизма.
• Наконец, мы должны показать, что каждой неприводимой системе корней соответствует соответствующая простая алгебра Ли. Это утверждение очевидно для систем корней типов A, B, C и D, для которых ассоциированные алгебры Ли являются классическими алгебрами Ли . Тогда можно будет анализировать исключительные алгебры в индивидуальном порядке. В качестве альтернативы можно разработать систематическую процедуру построения алгебры Ли из корневой системы, используя соотношения Серра .

О связях между исключительными системами корней и их группами Ли и алгебрами Ли см. E ₈ , E ₇ , E ₆ , F ₄ и G ₂ .

Свойства неприводимых корневых систем

Ф	| Ф |	| Ф < |	я	Д	| В |
А н ( п ≥ 1)	п ( п + 1)			п + 1	( п + 1)!
Бн ≥ ( n 2)	22н 2	22н	2	2	2 н н !
С н ( п ≥ 3)	22н 2	2n - 1 ( п )	2 п -1	2	2 н н !
Д н ( п ≥ 4)	2n - 1 ( п )			4	2 п -1 н !
EЕ6	72			3	51840
E 7	126			2	2903040
EЕ8	240			1	696729600
FF4	48	24	4	1	1152
Г 2	12	6	3	1	12

Неприводимые корневые системы названы в соответствии с соответствующими связными диаграммами Дынкина. Существует четыре бесконечных семейства (An _, Bn _, Cn _и Dn _, называемые классическими корневыми системами ) и пять исключительных случаев ( исключительные корневые системы ). Нижний индекс указывает ранг корневой системы.

В неприводимой корневой системе может быть не более двух значений длины ( α , α ) ^1/2 , соответствующие коротким и длинным корням. Если все корни имеют одинаковую длину, они по определению считаются длинными, а корневая система называется просто ажурной ; это происходит в случаях A, D и E. Любые два корня одинаковой длины лежат в одной и той же орбите группы Вейля. В непростых случаях B, C, G и F решетка корней натянута на короткие корни, а длинные корни натянуты на подрешетку, инвариантную относительно группы Вейля, равную r ² /2 раза больше решетки кокорней, где r — длина длинного корня.

В соседней таблице | Φ ^< | обозначает количество коротких корней, I обозначает индекс в решетке корней подрешетки, порожденной длинными корнями, D обозначает определитель матрицы Картана и | Вт | обозначает порядок группы Вейля .

Явное построение неприводимых корневых систем.

н _​

Модель $A_{3}$ корневая система в системе Zometool

Простые корни в A ₃

	и 1	eе2	3 ​	4 ​
1 ​	1	−1	0	0
2 ​	0	1	−1	0
3 ​	0	0	1	−1

Пусть E — подпространство в R ^{п +1} для которых сумма координат равна 0, и пусть Φ - набор векторов в E длины √ 2 , которые являются целыми векторами, т. е. имеют целые координаты в R ^{п +1} . Такой вектор должен иметь все координаты, кроме двух, равных 0, одну координату, равную 1, и одну, равную -1, поэтому существует n ² + n корней всего. Одним из вариантов простых корней, выраженных в стандартном базисе, является α _i = e _i − e _{i +1} для 1 ≤ i ≤ n .

Отражение аналогично σi _{перпендикулярную} через гиперплоскость, αi , _-й перестановке соседних i - й и ( i +1) координат . Такой транспозиции генерируют полную группу перестановок . Для соседних простых корней σ _i ( α _{i +1} ) = α _{i +1} + α _i = σ _{i +1} ( α _i ) = α _i + α _{i +1} , то есть отражение эквивалентно добавлению числа, кратного 1; но отражение простого корня перпендикулярно несмежному простому корню оставляет его неизменным, отличаясь кратно 0.

Решетку корней An _An , то есть решетку, порожденную корнями проще _, всего описать как набор целочисленных векторов в R ^{п +1} сумма компонентов которого равна нулю.

Корневая решетка A ₂ представляет собой расположение вершин треугольной мозаики .

Корневая решетка А 3 _{гранецентрированная} известна кристаллографам как кубическая (или кубическая плотноупакованная ) решетка. Это расположение вершин тетраэдрически-октаэдрических сот .

Корневую систему А ₃ (как и другие корневые системы третьего ранга) можно смоделировать в конструкторе Zometool .

В общем, An _{корневая решетка} — это расположение вершин n -мерной симплициальной соты .

Б _н

Простые корни в B ₄

	и 1	eе2	3 ​	4 ​
1 ​	1	−1	0	0
2 ​	0	1	−1	0
3 ​	0	0	1	−1
4 ​	0	0	0	1

Пусть Е = R ^н , и пусть Φ состоит из всех целых векторов из E длины 1 или √ 2 . Общее число корней равно 2 n ² . Одним из вариантов простых корней является α _i = e _i – e _{i +1} для 1 ≤ i ≤ n – 1 (вышеупомянутый выбор простых корней для A _{n −1} ) и более короткий корень α _n = e _n .

Отражение σ _n через гиперплоскость, перпендикулярную короткому корню α _n, является, конечно, просто отрицанием n- й координаты. длинного простого корня αn _{− 1} σn _{− 1} ( αn _Для ) = + ₎ αn − _{1 ,} но для отражения, перпендикулярного короткому корню, σn ₌ ( αn _{− 1} αn αn _{− 1} + 2 α _n , разница кратна 2 вместо 1.

Решетка корней Bn _Bn , то есть решетка, порожденная корнями , _{состоит} из всех целочисленных векторов.

B ₁ изоморфен A ₁ посредством масштабирования на √ 2 и, следовательно, не является отдельной корневой системой.

С _н

Корневая система B ₃ , C ₃ и A ₃ = D ₃ как точки внутри куба и октаэдра.

Простые корни в C ₄

	и 1	eе2	3 ​	4 ​
1 ​	1	−1	0	0
2 ​	0	1	−1	0
3 ​	0	0	1	−1
4 ​	0	0	0	2

Пусть Е = R ^н , и пусть Φ состоит из всех целых векторов из E длины √ 2 вместе со всеми векторами вида 2 λ , где λ — целочисленный вектор длины 1. Общее число корней равно 2 n ² . Один из вариантов простых корней: α _i = e _i − e _{i +1} для 1 ≤ i ≤ n − 1 (вышеупомянутый выбор простых корней для A _{n −1} ), и более длинный корень α _n = 2 e _n . Отражение σ _n ( α _{n −1} ) = α _{n −1} + α _n , но σ _{n −1} ( α _n ) = α _n + 2 α _{n −1} .

Решетка корней C _n , то есть решетка, порожденная корнями C _n , состоит из всех целочисленных векторов, сумма компонентов которых дает четное целое число.

C ₂ изоморфен B ₂ посредством масштабирования на √ 2 и поворота на 45 градусов и, следовательно, не является отдельной корневой системой.

Д _н

Простые корни в D ₄

	и 1	eе2	3 ​	4 ​
1 ​	1	−1	0	0
2 ​	0	1	−1	0
3 ​	0	0	1	−1
4 ​	0	0	1	1

Пусть Е = R ^н , и пусть Φ состоит из всех целых векторов из E длины √ 2 . Общее количество корней равно 2 n ( n − 1) . Одним из вариантов простых корней является α _i = e _i − e _{i +1} для 1 ≤ i ≤ n − 1 (вышеупомянутый выбор простых корней для A _{n −1} ) вместе с α _n = e _{n −1} + e _n .

Отражение через гиперплоскость, перпендикулярную α _n, аналогично транспонированию и отрицанию соседних n -й и ( n − 1)-й координат. Любой простой корень и его отражение, перпендикулярное другому простому корню, отличаются от второго корня кратным 0 или 1, а не большим кратным.

Решетка корней D _n , то есть решетка, порожденная корнями D _n , состоит из всех целочисленных векторов, сумма компонентов которых дает четное целое число. Это то же самое, что корней Cn _{решетка} .

Корни Dn _{диаграммы} выражаются как вершины выпрямленного n - ортоплекса , Кокстера-Дынкина : ... . 2 − n ( n 1) вершин находятся в середине ребер n -ортоплекса.

D ₃ совпадает с A ₃ и поэтому не является отдельной корневой системой. Двенадцать корневых векторов D ₃ выражаются как вершины , конструкция более низкой симметрии кубооктаэдра .

D ₄ обладает дополнительной симметрией, называемой тройственностью . Двадцать четыре корневых вектора D ₄ выражаются как вершины , конструкция с более низкой симметрией 24-элементного .

E ₆ , E ₇ , E ₈

72 вершины из 1 22 представляют корневые векторы E 6 (Зеленые узлы удвоены в этой проекции плоскости Кокстера E6)	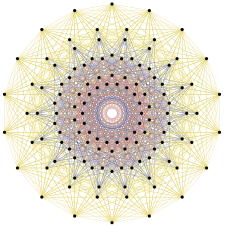126 вершин из 2 31 представляют собой корневые векторы E 7.	240 вершин из 4 21 представляют корневые векторы E 8

• Корневая система E ₈ — это любой набор векторов из R ⁸ что соответствует следующему набору: $$D_{8}\cup \left\{{\frac {1}{2}}\left(\sum _{i=1}^{8}\varepsilon _{i}\mathbf {e} _{i}\right):\varepsilon _{i}=\pm 1,\,\varepsilon _{1}\cdots \varepsilon _{8}=+1\right\}.$$

Корневая система насчитывает 240 корней. Только что перечисленный набор представляет собой набор векторов длины √ 2 в корневой решетке E8, также известной как решетка E8 или Γ ₈ . Это набор точек в R ⁸ такой, что:

1. все координаты являются целыми числами или все координаты являются полуцелыми числами (смесь целых и полуцелых чисел не допускается), и
2. сумма восьми координат является четным целым числом .

Таким образом, $$E_{8}=\left\{\alpha \in \mathbb {Z} ^{8}\cup \left(\mathbb {Z} +{\tfrac {1}{2}}\right)^{8}:|\alpha |^{2}=\sum \alpha _{i}^{2}=2,\,\sum \alpha _{i}\in 2\mathbb {Z} .\right\}$$

• Корневая система E7 _{перпендикулярных} — это набор векторов из , _E8 фиксированному корню E8 _из . Корневая система Е ₇ насчитывает 126 корней.
• Корневая система E ₆ не является набором векторов из E ₇ , перпендикулярных фиксированному корню из E ₇ , действительно, можно получить D ₆ таким образом . Однако E6 _, подсистемой E8 _корням перпендикулярной двум соответствующим образом выбранным E8 _{является} . Корневая система Е ₆ имеет 72 корня.

Простые корни из E ₈ : четные координаты

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	1	1	0
− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠

Альтернативное описание решетки E8 _, которое иногда бывает удобным, состоит в том, что множество Γ'8 _всех точек в R ⁸ такой, что

• все координаты целые числа, а сумма координат четная, или
• все координаты полуцелые, а сумма координат нечетная.

Решетки _Г8 Г'8 _​ изоморфны ; и от одной к другой можно перейти, меняя знаки любого нечетного числа координат. Решетку Г8 _иногда называют четной системой координат для Е8 _, а решетку Г'8 _{называют} нечетной системой координат .

Один из вариантов простых корней для E ₈ в четной системе координат со строками, упорядоченными по порядку узлов в альтернативных (неканонических) диаграммах Дынкина (выше):

α _i = e _i − e _{i +1} , для 1 ≤ i ≤ 6, и

α ₇ = е ₇ + е ₆

(вышеупомянутый выбор простых корней для D ₇ ) вместе с $${\boldsymbol {\alpha }}_{8}={\boldsymbol {\beta }}_{0}=-{\frac {1}{2}}\sum _{i=1}^{8}\mathbf {e} _{i}=(-1/2,-1/2,-1/2,-1/2,-1/2,-1/2,-1/2,-1/2).$$

Простые корни в E ₈ : нечетные координаты

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	0	1	−1
− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	⁠ 1 / 2 ⁠	⁠ 1 / 2 ⁠	⁠ 1 / 2 ⁠

Один из вариантов простых корней для E ₈ в нечетной системе координат со строками, упорядоченными по порядку узлов в альтернативных (неканонических) диаграммах Дынкина (выше)

α _я знак равно е _я - е _{я +1} , для 1 ≤ я ≤ 7

(вышеупомянутый выбор простых корней для A ₇ ) вместе с

α ₈ = β ₅ , где

${\textstyle {\boldsymbol {\beta }}_{j}={\frac {1}{2}}\left(-\sum _{i=1}^{j}e_{i}+\sum _{i=j+1}^{8}e_{i}\right).}$

(Использование β ₃ дало бы изоморфный результат. Использование β _1,7 или β _2,6 просто дало бы A ₈ или D ₈ . Что касается β ₄ , его сумма координат равна 0, и то же самое верно для α _{1.. .7} , поэтому они охватывают только 7-мерное подпространство, для которого сумма координат равна 0, на самом деле −2 β ₄ имеет координаты (1,2,3,4,3,2,1) в базисе ( α _i ) .)

Поскольку перпендикулярность к α ₁ означает, что первые две координаты равны, E ₇ тогда является подмножеством E ₈ , где первые две координаты равны, и аналогично E ₆ является подмножеством E ₈ , где первые три координаты равны. Это облегчает явное определение E ₇ и E ₆ как

E ₇ = { α ∈ Z ⁷ ∪ ( Z +1/2) ⁷ : Сай я _​ ² + 1 _​ ² = 2, Σ α _i + α ₁ ∈ 2 Z },

E ₆ = { α ∈ Z ⁶ ∪ ( Z +1/2) ⁶ : Сай я _​ ² + 2 а ₁ ² знак равно 2, Σ α _я + 2 α ₁ ∈ 2 Z }

удаление α1 _, а затем α2 _, дает наборы простых корней для E7 _{Обратите внимание} и E6 _что . множества простых корней находятся в других E7 _{подпространствах} и E6 _эти пространства E8 _, написанные выше, поскольку они не ортогональны α1 _Однако или α2 _чем .

F_F4

Простые корни в F ₄

	и 1	eе2	3 ​	4 ​
1 ​	1	−1	0	0
2 ​	0	1	−1	0
3 ​	0	0	1	0
4 ​	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠	− ⁠ 1 / 2 ⁠

48-корневые векторы F4, определяемые вершинами 24-ячейки и ее двойственной ячейки, рассматриваемые в плоскости Кокстера.

Для F ₄ пусть E = R ⁴ и пусть Φ обозначает набор векторов α длины 1 или √ 2 таких, что все координаты 2α являются целыми числами и либо все четные, либо все нечетные. В этой системе 48 корней. Один из вариантов простых корней: выбор простых корней, указанный выше для B ₃ , плюс ${\textstyle {\boldsymbol {\alpha }}_{4}=-{\frac {1}{2}}\sum _{i=1}^{4}e_{i}}$.

Корневая решетка F ₄ , то есть решетка, порожденная корневой системой F ₄ , представляет собой множество точек в R ⁴ так, что либо все координаты являются целыми числами , либо все координаты являются полуцелыми числами (смесь целых и полуцелых чисел не допускается). Эта решетка изоморфна решетке кватернионов Гурвица .

Г ₂

Простые корни из G ₂

	и 1	eе2	3 ​
1 ​	1	−1	0
б	−1	2	−1

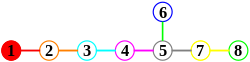
Корневая система G ₂ имеет 12 корней, образующих вершины гексаграммы . Смотрите картинку выше .

Один из вариантов простых корней: ( α ₁ , β = α ₂ − α ₁ ), где α _i = e _i − e _{i +1} для i = 1, 2 — это указанный выше выбор простых корней для A ₂ .

Решетка корней G2 _G2 решетка, порожденная корнями , _{аналогична} решетке корней A2 _{, т. е .} .

Корневой посет

Диаграмма Хассе E6 корневого ЧУМ с метками ребер, обозначающими добавленное простое положение корня

Множество положительных корней естественным образом упорядочивается, говоря, что $\alpha \leq \beta$ тогда и только тогда, когда $\beta -\alpha$ является неотрицательной линейной комбинацией простых корней. Этот посет оценивается ​ по ${\textstyle \deg \left(\sum _{\alpha \in \Delta }\lambda _{\alpha }\alpha \right)=\sum _{\alpha \in \Delta }\lambda _{\alpha }}$, и обладает многими замечательными комбинаторными свойствами, одно из которых состоит в том, что по этому ЧУ можно определить степени фундаментальных инвариантов соответствующей группы Вейля. Граф Хассе представляет собой визуализацию упорядочения корневого ЧУУ.

См. также

• Классификация ADE
• Аффинная корневая система
• Диаграмма Кокстера – Дынкина
• Группа Коксетера
• Матрица Кокстера
• Диаграмма Дынкина
• корневая дата
• Полупростая алгебра Ли
• Веса в теории представлений полупростых алгебр Ли
• Система корней полупростой алгебры Ли
• Группа Вейля

Ссылки

• Адамс, Дж. Ф. (1983), Лекции о группах лжи , University of Chicago Press, ISBN  0-226-00530-5
• Бурбаки, Николя (2002), Группы Ли и алгебры Ли, главы 4–6 (перевод с французского оригинала 1968 года Эндрю Прессли) , Элементы математики, Springer-Verlag, ISBN  3-540-42650-7 . Классический справочник по корневым системам.
• Бурбаки, Николя (1998). Элементы истории математики . Спрингер. ISBN  3540647678 .
• Коулман, AJ (лето 1989 г.), «Величайшая математическая статья всех времен», The Mathematical Intelligencer , 11 (3): 29–38, doi : 10.1007/bf03025189 , S2CID   35487310
• Холл, Брайан К. (2015), Группы Ли, алгебры Ли и представления: элементарное введение , Тексты для выпускников по математике, том. 222 (2-е изд.), Спрингер, ISBN  978-3319134666
• Хамфрис, Джеймс (1972). Введение в алгебры Ли и теорию представлений . Спрингер. ISBN  0387900535 .
• Хамфрис, Джеймс (1992). Группы отражения и группы Кокстера . Издательство Кембриджского университета. ISBN  0521436133 .
• Киллинг, Вильгельм (июнь 1888 г.). «Композиция непрерывных конечных групп преобразований» . Математические летописи . 31 (2): 252–290. дои : 10.1007/BF01211904 . S2CID   120501356 . Архивировано из оригинала 05 марта 2016 г.
  • - (март 1888 г.). «Часть 2» . Математика. Энн . 33 (1): 1–48. дои : 10.1007/BF01444109 . S2CID   124198118 .
  • - (март 1889 г.). «Часть 3» . Математика. Энн . 34 (1): 57–122. дои : 10.1007/BF01446792 . S2CID   179177899 . Архивировано из оригинала 21 февраля 2015 г.
  • - (июнь 1890 г.). «Часть 4» . Математика. Энн . 36 (2): 161–189. дои : 10.1007/BF01207837 . S2CID   179178061 .
• Кац, Виктор Г. (1990). Бесконечномерные алгебры Ли (3-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-46693-6 .
• Спрингер, Т.А. (1998). Линейные алгебраические группы (2-е изд.). Биркхойзер. ISBN  0817640215 .

Дальнейшее чтение

• Дынкин, Е.Б. (1947). «Строение полупростых алгебр» . Успехи мат. Наук . 2 (на русском языке). 4 (20): 59–127. МР   0027752 .