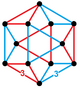
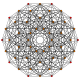
Симплициальные соты

${\tilde {A}}_{2}$	${\tilde {A}}_{3}$
Треугольная плитка	Тетраэдрально-октаэдрические соты
С красными и желтыми равносторонними треугольниками.	С голубыми и желтыми тетраэдрами , а также красными выпрямленными тетраэдрами ( октаэдрами ).

В геометрии симплициальные соты (или $n$ -симплексные соты ) представляют собой размерную бесконечную серию сот , основанную на ${\tilde {A}}_{n}$ Симметрия аффинной группы Кокстера . Он представлен диаграммой Кокстера-Динкина в виде циклического графа из $n + 1$ узлов с одним окольцованным узлом. Он состоит из $n$ - симплексных граней вместе со всеми выпрямленными $n$ -симплексами. Его можно рассматривать как $n$ - мерную гиперкубическую соту , разделенную по всем гиперплоскостям. $x+y+\cdots \in \mathbb {Z}$ , затем растягивается вдоль его главной диагонали до тех пор, пока симплексы на концах гиперкуба не станут правильными. Вершинная фигура представляет $n$ - симплексных сот собой расширенный $n$ - симплекс .

В двух измерениях соты представляют собой треугольную мозаику с графом Коксетера. заполнение плоскости треугольниками поочередного цвета. В трех измерениях он представляет собой тетраэдрически-октаэдрические соты с графом Коксетера. заполнение пространства попеременно тетраэдрическими и октаэдрическими ячейками. В 4-х измерениях это называется 5-ячеечной сотой с графом Кокстера. , с 5-клеточными и выпрямленными 5-клеточными гранями. В пяти измерениях это называется 5-симплексными сотами с графом Коксетера. , заполнение пространства 5-симплексными , выпрямленными 5-симплексными и двуисправленными 5-симплексными гранями. В шести измерениях это называется 6-симплексными сотами с графом Коксетера. , заполняя пространство 6-симплексными , выпрямленными 6-симплексными и биректифицированными 6-симплексными гранями.

По размеру

н	${\tilde {A}}_{2+}$	Тесселяция	Вершинная фигура	Фасетов на фигуру вершины	Вершин на фигуру вершины	Краевая фигура
1	${\tilde {A}}_{1}$	Апейрогон	Отрезок линии	2	2	Точка
2	${\tilde {A}}_{2}$	Треугольная плитка 2-симплекс сотовый	Шестиугольник (усеченный треугольник)	3+3 треугольника	6	Отрезок линии
3	${\tilde {A}}_{3}$	Тетраэдрально-октаэдрические соты 3-симплексные соты	Кубооктаэдр (Скантелляционный тетраэдр)	4+4 тетраэдра 6 выпрямленных тетраэдров	12	Прямоугольник
4	${\tilde {A}}_{4}$	4-симплексные соты	Ранцинированный 5-клеточный	5+5 5-клеток 10+10 выпрямленные 5-клеточные	20	Треугольная антипризма
5	${\tilde {A}}_{5}$	5-симплексные соты	Стерический 5-симплекс	6+6 5-симплекс 15+15 выпрямленный 5-симплекс 20 биректифицированных 5-симплексных	30	Тетраэдрическая антипризма
6	${\tilde {A}}_{6}$	6-симплексные соты	Пятеричный 6-симплекс	7+7 6-симплекс 21+21 выпрямленный 6-симплекс 35+35 биректифицированный 6-симплекс	42	4-симплексная антипризма
7	${\tilde {A}}_{7}$	7-симплексные соты	Шестигранный 7-симплекс	8+8 7-симплекс 28+28 выпрямленный 7-симплекс 56+56 биректифицированный 7-симплекс 70 триректифицированных 7-симплексных	56	5-симплексная антипризма
8	${\tilde {A}}_{8}$	8-симплексные соты	Гептеллированный 8-симплекс	9+9 8-симплекс 36+36 выпрямленный 8-симплекс 84+84 биректифицированный 8-симплекс 126+126 триректифицированный 8-симплекс	72	6-симплексная антипризма
9	${\tilde {A}}_{9}$	9-симплексные соты	Восьмеричный 9-симплекс	10+10 9-симплекс 45+45 выпрямленный 9-симплекс 120+120 биректифицированный 9-симплексный 210+210 триректифицированный 9-симплекс 252 четырехнаправленный 9-симплексный	90	7-симплексная антипризма
10	${\tilde {A}}_{10}$	10-симплексные соты	Объединенный 10-симплекс	11+11 10-симплекс 55+55 выпрямленный 10-симплекс 165+165 биректифицированный 10-симплекс 330+330 триректифицированный 10-симплекс 462+462 четырехнаправленный 10-симплексный	110	8-симплексная антипризма
11	${\tilde {A}}_{11}$	11-симплексные соты	...	...	...	...

Проекция путем складывания

(2n-1)-симплексные соты и 2n-симплексные соты можно спроецировать в n-мерные гиперкубические соты с помощью операции геометрического складывания , которая отображает две пары зеркал друг в друга, имеющих одинаковое расположение вершин :

${\tilde {A}}_{2}$	${\tilde {A}}_{4}$	${\tilde {A}}_{6}$	${\tilde {A}}_{8}$	${\tilde {A}}_{10}$	...
${\tilde {A}}_{3}$	${\tilde {A}}_{3}$	${\tilde {A}}_{5}$	${\tilde {A}}_{7}$	${\tilde {A}}_{9}$	...
${\tilde {C}}_{1}$	${\tilde {C}}_{2}$	${\tilde {C}}_{3}$	${\tilde {C}}_{4}$	${\tilde {C}}_{5}$	...

Поцелуйный номер

Эти соты, рассматриваемые как касательные n-сферы, расположенные в центре каждой вершины сот, имеют фиксированное количество контактирующих сфер и соответствуют количеству вершин на рисунке вершин . Это представляет собой наибольшее количество поцелуев для 2-го и 3-го измерений, но не соответствует более высоким измерениям. В двухмерном измерении треугольная мозаика определяет круговую упаковку из 6 касательных сфер, расположенных в правильном шестиугольнике, а в трех измерениях имеется 12 касательных сфер, расположенных в кубооктаэдрической конфигурации. Для измерений от 4 до 8 числа поцелуев составляют 20 , 30 , 42 , 56 и 72 сферы, а наибольшие решения — 24, 40, 72, 126 и 240 сфер соответственно.

См. также

Ссылки

Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Бранко Грюнбаум , Равномерные разбиения трехмерного пространства. Геомбинаторика 4 (1994), 49–56.
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10] (1.9 Равномерные пространственные заполнения)
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	0 _[3]	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	0 _[4]	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	0 _[5]	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	0 _[6]	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	0 _[7]	д ₇	hδ ₇	квартал ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	0 _[8]	д ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	0 _[9]	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	0 _[10]	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	0 _[11]	д ₁₁	HD ₁₁	11 _{квартал}
И ^{п -1}	Равномерный ( n -1)- сотовый	0 _{[ н ]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁