Кубические соты

Кубические соты

Тип	Обычные соты
Семья	Гиперкубические соты
Индексирование ^[1]	Дж _11,15 , А ₁ В ₁ , Г ₂₂
Символ Шлефли	{4,3,4}
Диаграмма Кокстера
Тип ячейки	{4,3}
Тип лица	квадрат {4}
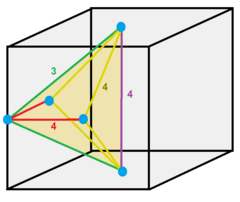
Вершинная фигура	октаэдр
Космическая группа Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Группа Коксетера	${\tilde {C}}_{3}$ , [4,3,4]
Двойной	самодвойственный Клетка:
Характеристики	Вершинно-транзитивный , регулярный

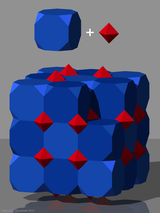
Кубические соты или кубическая ячейка — единственная правильная правильная мозаика , заполняющая пространство (или соты ), в евклидовом трехмерном пространстве, состоящем из кубических ячеек. Он имеет по 4 куба вокруг каждого ребра и по 8 кубов вокруг каждой вершины. Его вершинная фигура — правильный октаэдр . Это самодвойственная мозаика с символом Шлефли {4,3,4}. Джон Хортон Конвей назвал эти соты кубилью .

Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Связанные соты

Это часть многомерного семейства сот гиперкуба с символами Шлефли формы {4,3,...,3,4}, начиная с квадратной мозаики {4,4} на плоскости.

Это одна из 28 однородных сот, в которых используются выпуклые однородные многогранные ячейки.

Изометрии простых кубических решеток

Простые кубические решетки могут быть искажены до более низких симметрий, представленных более низкими кристаллическими системами:

Кристаллическая система	Моноклиника Триклиника	орторомбический	четырехугольный	Ромбоэдрический	Кубический
Элементарная ячейка	Параллелепипед	Прямоугольный кубоид	Квадратный кубоид	Треугольный трапецоэдр	Куб
Группа точек Заказ Подгруппа вращения	[ ], (*) Заказ 2 [ ] ⁺, (1)	[2,2], (*222) Заказать 8 [2,2] ⁺, (222)	[4,2], (*422) Заказ 16 [4,2] ⁺, (422)	[3], (*33) Заказ 6 [3] ⁺, (33)	[4,3], (*432) Заказ 48 [4,3] ⁺, (432)
Диаграмма
Космическая группа Подгруппа вращения	Вечер (6) П1 (1)	Пммм (47) П222 (16)	П4/ммм (123) П422 (89)	3 миллиона рэндов (160) Р3 (146)	ПМ 3 м (221) П432 (207)
Обозначение Кокстера	-	[∞] _а ×[∞] _б ×[∞] _c	[4,4] _а ×[∞] _в	-	[4,3,4] _а
Диаграмма Кокстера	-			-

Равномерные раскраски

Существует большое количество однородных раскрасок , полученных из разных симметрий. К ним относятся:

Обозначение Кокстера Космическая группа	Диаграмма Кокстера	Символ Шлефли	Цвета по буквам
[4,3,4] ПМ 3 м (221)	=	{4,3,4}	1: аааа/аааа
[4,3 ^1,1] = [4,3,4,1 ⁺] Фм 3 м (225)	=	{4,3 ^1,1}	2: отец/отец
[4,3,4] ПМ 3 м (221)		т _0,3 {4,3,4}	4: АБВ/BCCD
[[4,3,4]] ПМ 3 м (229)		т _0,3 {4,3,4}	4: абб/ббба
[4,3,4,2,∞]	или	{4,4}×t{∞}	2: аааа/бббб
[4,3,4,2,∞]		т ₁ {4,4}×{∞}	2: в/в
[∞,2,∞,2,∞]		т{∞}×t{∞}×{∞}	4: абкд/абкд
[∞,2,∞,2,∞] = [4,(3,4) ^*]	=	т{∞}×t{∞}×t{∞}	8: abcd/efgh

Прогнозы

Кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии. Форма высшей (шестиугольной) симметрии образует треугольную мозаику . Проекция квадратной симметрии образует квадратную мозаику .

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Связанные многогранники и соты

Он связан с правильным 4-многогранным тессерактом , символом Шлефли {4,3,3}, который существует в 4-мерном пространстве и имеет только 3 куба вокруг каждого края. Это также связано с кубическими сотами пятого порядка , символом Шлефли {4,3,5}, гиперболического пространства с пятью кубами вокруг каждого края.

Он представляет собой последовательность полихор и сот с восьмигранными вершинными фигурами .

{p,3,4} обычные соты
Space	S³	E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Это последовательность правильных многогранников и сот с кубическими ячейками .

{4,3,p} обычные соты
Space	S³	E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{p,3,p} обычные соты
Space	S³	Euclidean E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Связанные многогранники

Кубические соты имеют более низкую симметрию, чем сморщенные кубические соты, с кубиками двух размеров . Конструкцию с двойной симметрией можно построить, поместив маленький куб в каждый большой куб, в результате чего получатся неоднородные соты с кубами , квадратными призмами и прямоугольными трапециями (куб с D _2d симметрией ). Его вершинная фигура представляет собой треугольную пирамиду, боковые грани которой дополнены тетраэдрами.

Двойная ячейка

Полученные соты можно чередовать, чтобы получить еще одну неоднородную соту с правильными тетраэдрами , двумя видами тетрагональных дисфеноидов, треугольными пирамидами и клиноидами. Его вершинная фигура имеет симметрию C _3v и имеет 26 треугольных граней, 39 ребер и 15 вершин.

Связанные евклидовы мозаики

[4,3,4], генерирует Группа Коксетера 15 перестановок однородных мозаик, 9 из которых имеют четкую геометрию, включая чередующиеся кубические соты. Расширенные кубические соты (также известные как продолговатые кубические соты) геометрически идентичны кубическим сотам.

Соты C3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

[4,3 ^1,1], генерирует Группа Коксетера 9 перестановок однородных мозаик, 4 из которых имеют четкую геометрию, включая чередующиеся кубические соты.

Соты B3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

Эти соты являются одними из пяти различных однородных сот. ^[2] построенный ${\tilde {A}}_{3}$ Группа Кокстера . Симметрию можно умножить на симметрию колец в диаграммах Кокстера – Дынкина :

Соты А3
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

Ректифицированный кубический сот

Ректифицированные кубические соты
Тип	Равномерные соты
Символ Шлефли	r{4,3,4} или t ₁ {4,3,4} г{4,3 ^1,1} 2r{4,3 ^1,1} г{3 ^[4]}
Диаграммы Кокстера	= = = = =
Клетки	г{4,3} {3,4}
Лица	треугольник {3} квадрат {4}
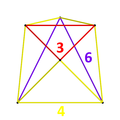
Вершинная фигура	квадратная призма
Космическая группа Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Группа Коксетера	${\tilde {C}}_{3}$ , [4,3,4]
Двойной	сплюснутый октаэдрилл Клетка:
Характеристики	Вершинно-транзитивный , реберно-транзитивный

Выпрямленные кубические соты или выпрямленные кубические ячейки представляют собой однородную мозаику , заполняющую пространство (или соты ) в евклидовом трехмерном пространстве. Он состоит из октаэдров и кубооктаэдров в соотношении 1:1, с квадратной фигурой вершины призмы .

Джон Хортон Конвей называет эту соту кубооктаэдрилом , а ее двойник — сплюснутым октаэдрилем .

Прогнозы

Выпрямленные кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Существует четыре однородные раскраски ячеек этой соты с отражательной симметрией, перечисленные по их группе Кокстера и конструкции Витхоффа названию , а также диаграмме Кокстера ниже.

Симметрия	[4,3,4] ${\tilde {C}}_{3}$	[1 ⁺,4,3,4] [4,3 ^1,1], ${\tilde {B}}_{3}$	[4,3,4,1 ⁺] [4,3 ^1,1], ${\tilde {B}}_{3}$	[1 ⁺,4,3,4,1 ⁺] [3 ^[4]], ${\tilde {A}}_{3}$
Космическая группа	ТЧ 3 м (221)	FM 3 м (225)	FM 3 м (225)	Ф 4 3м (216)
Раскраска
Коксетер диаграмма
Коксетер диаграмма
Вершинная фигура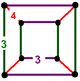
Вертекс фигура симметрия	Д _{4 часа} [4,2] (*224) заказать 16	Д _{2 часа} [2,2] (*222) заказать 8	С _4В [4] (*44) заказать 8	С _{2 в} [2] (*22) заказать 4

Эти соты можно разделить на тригексагональные плоскости мозаики, используя шестиугольные центры кубооктаэдров, создавая два треугольных купола . Эти чешуйчатые соты представлены диаграммой Кокстера. и символ s ₃ {2,6,3} с симметрией обозначений Кокстера [2 ⁺,6,3].

.

Связанные многогранники

Конструкцию с двойной симметрией можно создать, поместив октаэдры на кубооктаэдры, в результате чего получатся неоднородные соты с двумя видами октаэдров (правильные октаэдры и треугольные антипризмы). Вершинная фигура представляет собой квадратный бифрустум . Двойная состоит из вытянутых квадратных бипирамид .

Двойная ячейка

Усеченные кубические соты

Усеченные кубические соты
Тип	Равномерные соты
Символ Шлефли	t{4,3,4} или t _0,1 {4,3,4} т{4,3 ^1,1}
Диаграммы Кокстера	=
Тип ячейки	т{4,3} {3,4}
Тип лица	треугольник {3} восьмиугольник {8}
Вершинная фигура	равнобедренная квадратная пирамида
Космическая группа Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Группа Коксетера	${\tilde {C}}_{3}$ , [4,3,4]
Двойной	Пирамидиллия Клетка:
Характеристики	Вершинно-транзитивный

Усеченные кубические соты или усеченная кубическая ячейка — это однородная мозаика , заполняющая пространство (или соты ) в евклидовом трехмерном пространстве. Он составлен из усеченных кубов и октаэдров в соотношении 1:1, с равнобедренной квадратной пирамиды вершиной .

Джон Хортон Конвей называет эти соты усеченным кубильем и двойной пирамидилью .

Прогнозы

Усеченные кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Существует вторая равномерная раскраска, обусловленная отражательной симметрией групп Кокстера , вторая видна с попеременно окрашенными усеченными кубическими ячейками.

Строительство	Двукантелированный альтернативный куб	Усеченные кубические соты
Группа Коксетера	[4,3 ^1,1], ${\tilde {B}}_{3}$	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3 ^1,1]>
Космическая группа	FM 3 м	ТЧ 3 м
Раскраска
Диаграмма Кокстера	=
Вершинная фигура

Связанные многогранники

Конструкцию двойной симметрии можно создать, поместив октаэдры на усеченные кубы, в результате чего получится неоднородная сотовая структура с двумя видами октаэдров (правильные октаэдры и треугольные антипризмы) и двумя видами тетраэдров (тетрагональные дисфеноиды и двуугольные дисфеноиды). Вершинная фигура представляет собой квадратный купол октакиса.

Вершинная фигура

Двойная ячейка

Разрезанные кубические соты

Разрезанные кубические соты

Тип	Равномерные соты
Символ Шлефли	2т{4,3,4} т _1,2 {4,3,4}
Диаграмма Кокстера-Динкина
Клетки	т{3,4}
Лица	квадрат {4} шестигранник {6}
Краевая фигура	равнобедренный треугольник {3}
Вершинная фигура	тетрагональный дисфеноид
Группа симметрии Обозначение фиброфолда Обозначение Кокстера	Мне 3 метра (229) 8 ^тот:2 [[4,3,4]]
Группа Коксетера	${\tilde {C}}_{3}$ , [4,3,4]
Двойной	Сплюснутый тетраэдрилл Дисфеноидные тетраэдрические соты Клетка:
Характеристики	Вершинно-транзитивный , реберно-транзитивный , клеточно-транзитивный

Кубические соты с усеченными кусочками — это заполняющая пространство мозаика (или соты ) в евклидовом трехмерном пространстве, состоящая из усеченных октаэдров (или, что то же самое, кубов с усеченными битами ). Он имеет четыре усеченных октаэдра вокруг каждой вершины в виде дисфеноида тетрагональной фигуры вершины . Будучи полностью состоящим из усеченных октаэдров , он является клеточно-транзитивным . Он также транзитивен по ребрам , с двумя шестиугольниками и одним квадратом на каждом ребре, и транзитивен по вершинам . Это одна из 28 единых сот .

Джон Хортон Конвей называет эту соту усеченным октаэдрилом в своем списке архитектонической и катоптрической мозаики , а ее двойник называется сплющенным тетраэдрилом , также называемым дисфеноидным тетраэдрическим сотом . Хотя правильный тетраэдр не может сам по себе мозаику, этот двойственный тетраэдр имеет идентичные ячейки дисфеноидного тетраэдра с гранями равнобедренного треугольника .

Прогнозы

Кубические соты с усеченными кусочками можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии. Форма высшей (шестиугольной) симметрии образует неоднородную ромботригексагональную мозаику . Проекция квадратной симметрии образует две перекрывающиеся усеченные квадратные мозаики , которые объединяются вместе в квадратную мозаику со скошенными краями .

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Вершинной фигурой этой соты является дисфеноидный тетраэдр , а также тетраэдр Гурса ( фундаментальная область ) для ${\tilde {A}}_{3}$ Группа Кокстера . Эти соты имеют четыре однородные конструкции, причем усеченные октаэдрические ячейки имеют разные группы Кокстера и конструкции Витхоффа . Эти однородные симметрии можно представить, раскрасив по-разному ячейки в каждой конструкции.

Пять однородных раскрасок по клеточкам
Космическая группа	Мне 3 метра (229)	ПМ 3 м (221)	Фм 3 м (225)	Ф 4 3м (216)	Фд 3м (227)
Фибрифолд	8 ^тот:2	4 ⁻:2	2 ⁻:2	1 ^тот:2	2 ⁺:2
Группа Коксетера	${\tilde {C}}_{3}$ ×2 [[4,3,4]] =[4[3 ^[4]]] =	${\tilde {C}}_{3}$ [4,3,4] =[2[3 ^[4]]] =	${\tilde {B}}_{3}$ [4,3 ^1,1] =<[3 ^[4]]> =	${\tilde {A}}_{3}$ [3 ^[4]]	${\tilde {A}}_{3}$ ×2 [[3 ^[4]]] =[[3 ^[4]]]
Диаграмма Кокстера
усеченные октаэдры	1	1:1 :	2:1:1 : :	1:1:1:1 : : :	1:1 :
Вершинная фигура
Вертекс фигура симметрия	[2 ⁺,4] (заказ 8)	[2] (заказ 4)	[ ] (заказ 2)	[ ] ⁺ (заказ 1)	[2] ⁺ (заказ 2)
Изображение Раскрашено клетка

Связанные многогранники

Неоднородные варианты с симметрией [4,3,4] и двумя типами усеченных октаэдров можно удвоить, поместив два типа усеченных октаэдров для получения неоднородной соты с усеченными октаэдрами и шестиугольными призмами (как дитригональные трапезопризмы). Ее вершинной фигурой является C _2v -симметричная треугольная бипирамида .

Затем эти соты можно чередовать, чтобы получить еще одну неоднородную соту с пиритоэдрическими икосаэдрами , октаэдрами (как треугольные антипризмы) и тетраэдрами (как клиновидные). Его вершинная фигура имеет симметрию C _2v и состоит из 2 пятиугольников , 4 прямоугольников , 4 равнобедренных треугольников (разделенных на два набора по 2) и 4 разносторонних треугольников .

Чередованные битусеченные кубические соты

Чередованные битусеченные кубические соты
Тип	Выпуклые соты
Символ Шлефли	2с{4,3,4} 2с{4,3 ^1,1} ср{3 ^[4]}
Диаграммы Кокстера	= = =
Клетки	{3,3} с{3,3}
Лица	треугольник {3}
Вершинная фигура
Группа Коксетера	[[4,3 ⁺,4]], ${\tilde {C}}_{3}$
Двойной	Соты из десяти бубнов Клетка:
Характеристики	Вершинно-транзитивный , неоднородный

Чередованные кубические соты с усеченными кусочками или кубические соты с двукратными усечениями являются неоднородными, при этом конструкция с наивысшей симметрией отражает чередование однородных кубических сот с усеченными битами. Конструкция с более низкой симметрией включает в себя правильные икосаэдры в паре с золотыми икосаэдрами (с 8 равносторонними треугольниками в паре с 12 золотыми треугольниками). Есть три конструкции из трех связанных диаграмм Кокстера : , , и . Они обладают симметрией [4,3 ⁺,4], [4,(3 ^1,1) ⁺] и [3 ^[4]] ⁺ соответственно. Первую и последнюю симметрию можно удвоить как [[4,3 ⁺,4]] и [[3 ^[4]]] ⁺.

Эти соты представлены атомами бора α-ромбоэдрического кристалла . Центры икосаэдров расположены в ГЦК-положениях решетки. ^[3]

Пять однородных раскрасок
Космическая группа	Я 3 (204)	Вечер 3 (200)	Фм 3 (202)	Фд 3 (203)	Ф23 (196)
Фибрифолд	8 ^−о	4 ⁻	2 ⁻	2 ^о+	1 ^тот
Группа Коксетера	[[4,3 ⁺,4]]	[4,3 ⁺,4]	[4,(3 ^1,1) ⁺]	[[3 ^[4]]] ⁺	[3 ^[4]] ⁺
Диаграмма Кокстера
Заказ	двойной	полный	половина	четверть двойной	четверть

Кантелеллированные кубические соты

Кантелеллированные кубические соты
Тип	Равномерные соты
Символ Шлефли	рр{4,3,4} или т _0,2 {4,3,4} рр{4,3 ^1,1}
Диаграмма Кокстера	=
Клетки	рр{4,3} г{4,3} {}x{4}
Вершинная фигура	клин
Космическая группа Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$
Двойной	четверть сплюснутый октаэдрилл Клетка:
Характеристики	Вершинно-транзитивный

Зубчатые кубические соты или зубчатые кубические ячейки представляют собой однородную мозаику (или соты ), заполняющую пространство, в евклидовом трехмерном пространстве. Он состоит из ромбокубооктаэдров , кубооктаэдров и кубов в соотношении 1:1:3, с клиновидной вершинной фигурой .

Джон Хортон Конвей называет эти соты 2-RCO-трилью , а ее сплюснутым октаэдрилом с двойной четвертью .

Изображения

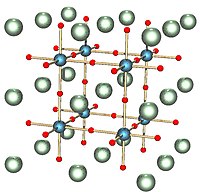	Она тесно связана со структурой перовскита , показанной здесь с кубической симметрией, с атомами, расположенными в центре ячеек этой соты.

Прогнозы

Зубчатые кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Существует вторая однородная раскраска, обусловленная отражательной симметрией групп Кокстера , вторая наблюдается с попеременно окрашенными ромбокубооктаэдрическими ячейками.

Равномерные раскраски вершин по ячейкам
Строительство	Усеченные кубические соты	Двукантелированный альтернативный куб
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3 ^1,1]>	[4,3 ^1,1], ${\tilde {B}}_{3}$
Космическая группа	ТЧ 3 м	FM 3 м
Диаграмма Кокстера
Раскраска
Вершинная фигура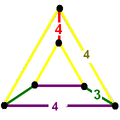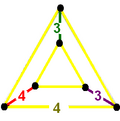
Вертекс фигура симметрия	[ ] заказ 2	[ ] ⁺ заказ 1

Связанные многогранники

Конструкцию двойной симметрии можно построить, поместив кубооктаэдры на ромбокубооктаэдры, в результате чего образуются выпрямленные кубические соты , приняв треугольные зазоры антипризмы за правильные октаэдры , пары квадратных антипризм и тетрагональные дисфеноиды нулевой высоты как компоненты кубооктаэдра . Другие варианты приводят к кубооктаэдрам , квадратным антипризмам , октаэдрам (как треугольные антиподии) и тетраэдрам (как тетрагональные дисфеноиды) с фигурой вершины, топологически эквивалентной кубу с треугольной призмой, прикрепленной к одной из его квадратных граней.

Четверть сплющенный октаэдрилл

Двойник зубчатых кубических сот называется четверть сплюснутым октаэдрилом , катоптрической мозаикой с диаграммой Коксетера. , содержащий грани из двух из четырех гиперплоскостей кубической [4,3,4] фундаментальной области.

Он имеет неправильные треугольные бипирамидальные ячейки, которые можно рассматривать как 1/12 куба, состоящие из центра куба, двух центров граней и двух вершин.

Канитусеченные кубические соты

Кантитусеченные кубические соты
Тип	Равномерные соты
Символ Шлефли	tr{4,3,4} или t _0,1,2 {4,3,4} тр{4,3 ^1,1}
Диаграмма Кокстера	=
Клетки	тр{4,3} т{3,4} {}x{4}
Лица	квадрат {4} шестигранник {6} восьмиугольник {8}
Вершинная фигура	зеркальная клиновидная кость
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$
Группа симметрии Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Двойной	треугольная пирамидиль Ячейки:
Характеристики	Вершинно-транзитивный

Кантиусеченные кубические соты или кантиусеченные кубические ячейки — это однородная, заполняющая пространство мозаика (или соты ) в евклидовом трехмерном пространстве, состоящая из усеченных кубооктаэдров , усеченных октаэдров и кубов в соотношении 1:1:3, с зеркальным клиновидным отростком. вершинная фигура .

Джон Хортон Конвей называет эту соту n-tCO-trill , а ее двойную треугольную пирамидилью .

Изображения

Вокруг каждой вершины существуют четыре ячейки:

Прогнозы

Скошенные кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Ячейки могут быть показаны в двух разных симметриях. Линейную диаграмму Кокстера можно нарисовать одним цветом для каждого типа ячеек. Форму раздвоенной диаграммы можно нарисовать с чередованием двух типов (цветов) ячеек усеченного кубооктаэдра .

Строительство	Кантитусеченный кубический	Всеусеченный альтернативный куб
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$ =<[4,3 ^1,1]>	[4,3 ^1,1], ${\tilde {B}}_{3}$
Космическая группа	ПМ 3 м (221)	Фм 3 м (225)
Фибрифолд	4 ⁻:2	2 ⁻:2
Раскраска
Диаграмма Кокстера
Вершинная фигура
Вертекс фигура симметрия	[ ] заказ 2	[ ] ⁺ заказ 1

Треугольная пирамидиль

Двойник изогнутых кубических сот называется треугольной пирамидилью с диаграммой Кокстера . . Эти сотовые ячейки представляют собой фундаментальные области ${\tilde {B}}_{3}$ симметрия.

Ячейка может составлять 1/24 поступательного куба с расположением вершин: два угла, центр грани и центр куба. Цвета и метки краев указывают, сколько ячеек существует по краю.

Связанные многогранники и соты

Это связано с косым апейроэдром с конфигурацией вершин 4.4.6.6, из которого удалены восьмиугольники и часть квадратов. Его можно рассматривать как построенный путем увеличения усеченных кубооктаэдрических ячеек или путем увеличения чередующихся усеченных октаэдров и кубов.

Два взгляда

Связанные многогранники

Конструкцию двойной симметрии можно построить, поместив усеченные октаэдры на усеченные кубооктаэдры, в результате чего получатся неоднородные соты с усеченными октаэдрами , шестиугольными призмами (как дитригональные трапезопризмы), кубами (как квадратные призмы), треугольными призмами (как C _2v -симметричные клинья). и тетраэдры (как тетрагональные дисфеноиды). Его вершинная фигура топологически эквивалентна октаэдру .

Вершинная фигура

Двойная ячейка

Чередованные скошенные кубические соты

Чередованные скошенные кубические соты
Тип	Выпуклые соты
Символ Шлефли	ср{4,3,4} ср{4,3 ^1,1}
Диаграммы Кокстера	=
Клетки	с{4,3} с{3,3} {3,3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура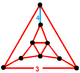
Группа Коксетера	[(4,3) ⁺,4]
Двойной	Клетка:
Характеристики	Вершинно-транзитивный , неоднородный

Перемежающиеся кантиусеченные кубические соты или курносые выпрямленные кубические соты содержат три типа ячеек: курносые кубы , икосаэдры (с Th _{симметрией} ), тетраэдры (как тетрагональные дисфеноиды) и новые тетраэдрические ячейки, созданные в промежутках.
Хотя он и не является однородным, конструктивно его можно представить в виде диаграмм Кокстера. или .

Несмотря на неоднородность, существует вариант с двумя длинами кромок, показанными ниже, одна из которых примерно на 4,3% больше другой. Курносые кубики в этом случае однородные, а остальные ячейки — нет.

Кантические курносые кубические соты

Ортоснуб кубические соты
Тип	Выпуклые соты
Символ Шлефли	2с ₀ {4,3,4}
Диаграммы Кокстера
Клетки	с2 _{ 3,4} с{3,3} {}х{3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура
Группа Коксетера	[4 ⁺,3,4]
Двойной	Клетка:
Характеристики	Вершинно-транзитивный , неоднородный

Кантические курносые кубические соты построены путем усечения усеченных октаэдров таким образом, что остаются только прямоугольники из кубов (квадратные призмы). Она не является однородной, но ее можно представить в виде диаграммы Кокстера. . Он имеет ромбокубооктаэдры с симметрией Th _{треугольные} ), икосаэдры (с симметрией Th ₍ ) и призмы (как клинья C _2v -симметрии), заполняющие пробелы. ^[4]

Связанные многогранники

Конструкцию двойной симметрии можно построить, поместив икосаэдры на ромбокубооктаэдры, в результате чего образуются неоднородные соты с икосаэдрами , октаэдрами (в виде треугольных антипризм), треугольными призмами (в виде C _2v -симметричных клиньев) и квадратными пирамидами .

Вершинная фигура

Двойная ячейка

Усеченные кубические соты

Усеченные кубические соты
Тип	Равномерные соты
Символ Шлефли	т _0,1,3 {4,3,4}
Диаграммы Кокстера
Клетки	рр{4,3} т{4,3} {}x{8} {}x{4}
Лица	треугольник {3} квадрат {4} восьмиугольник {8}
Вершинная фигура	равнобедренно-трапециевидная пирамида
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$
Космическая группа Обозначение фиброфолда	ПМ 3 м (221) 4 ⁻:2
Двойной	квадратная четверть пирамидиллы Клетка
Характеристики	Вершинно-транзитивный

Кубические соты с усеченными краями или кубические соты с усеченными элементами представляют собой однородную ) , заполняющую пространство мозаику (или соты , в евклидовом трехмерном пространстве. Он составлен из ромбокубооктаэдров , усеченных кубов , восьмиугольных призм и кубов в соотношении 1:1:3:3, с равнобедренно-трапециевидной пирамиды фигурой вершины .

Его название происходит от диаграммы Кокстера . с тремя кольцевыми узлами, представляющими 3 активных зеркала в конструкции Витхоффа с точки зрения ее отношения к правильным кубическим сотам.

Джон Хортон Конвей называет эти соты 1-RCO-трилью , а ее двойную квадратную четверть пирамидиллой .

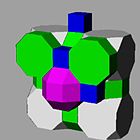Прогнозы

Кубические соты с усеченными краями можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый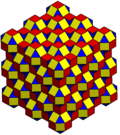
Рамка

Родственный косой апейроэдр

Существуют два связанных однородных косых апейроэдра с одинаковым расположением вершин , которые рассматриваются как граничные ячейки из подмножества ячеек. В одном есть треугольники и квадраты, а в другом — треугольники, квадраты и восьмиугольники.

Квадратная четверть пирамидиллы

Двойник кубических сот с усеченными краями называется квадратной четвертью пирамидиллы с диаграммой Коксетера . . Грани существуют в 3 из 4 гиперплоскостей [4,3,4], ${\tilde {C}}_{3}$ Группа Кокстера.

Ячейки представляют собой неправильные пирамиды, и их можно рассматривать как 1/24 куба с одним углом, одной средней точкой ребра, двумя центрами граней и центром куба.

Связанные многогранники

Конструкцию с двойной симметрией можно построить, поместив ромбокубооктаэдры на усеченные кубы, в результате чего получится неоднородная сота с ромбокубооктаэдрами , октаэдрами (как треугольные антипризмы), кубами (как квадратные призмы), двумя видами треугольных призм (оба C _2v -симметричные клинья). и тетраэдры (как двуугольные дисфеноиды). Ее вершинная фигура топологически эквивалентна расширенной треугольной призме .

Вершинная фигура

Двойная ячейка

Всеусеченные кубические соты

Всеусеченные кубические соты
Тип	Равномерные соты
Символ Шлефли	т _0,1,2,3 {4,3,4}
Диаграмма Кокстера
Клетки	тр{4,3} {}x{8}
Лица	квадрат {4} шестигранник {6} восьмиугольник {8}
Вершинная фигура	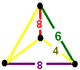филлический дисфеноид
Группа симметрии Обозначение фиброфолда Обозначение Кокстера	Мне 3 метра (229) 8 ^тот:2 [[4,3,4]]
Группа Коксетера	[4,3,4], ${\tilde {C}}_{3}$
Двойной	восьмая пирамидиль Клетка
Характеристики	Вершинно-транзитивный

Всеусеченные кубические соты или всеусеченные кубические ячейки представляют собой однородную мозаику (или соты ), заполняющую пространство, в евклидовом трехмерном пространстве. Он состоит из усеченных кубооктаэдров и восьмиугольных призм в соотношении 1:3, с филлической фигурой дисфеноида в вершине .

Джон Хортон Конвей называет эти соты b-tCO-trill , а их двойную восьмую пирамидилью .

Прогнозы

Всеусеченные кубические соты можно ортогонально спроецировать на евклидову плоскость с различными вариантами симметрии.

Ортогональные проекции
Симметрия	п6м (*632)	п4м (*442)	пмм (*2222)
Твердый
Рамка

Симметрия

Ячейки могут быть показаны в двух разных симметриях. Форма диаграммы Кокстера имеет два цвета усеченных кубооктаэдров и восьмиугольных призм . Симметрию можно удвоить, связав первую и последнюю ветви диаграммы Коксетера, которую можно показать одним цветом для всех усеченных кубооктаэдрических и восьмиугольных ячеек призмы.

Две однородные расцветки
Симметрия	${\tilde {C}}_{3}$ , [4,3,4]	${\tilde {C}}_{3}$ ×2, [[4,3,4]]
Космическая группа	ПМ 3 м (221)	Мне 3 метра (229)
Фибрифолд	4 ⁻:2	8 ^тот:2
Раскраска
Диаграмма Кокстера
Вершинная фигура

Связанные многогранники

Существуют два связанных однородных косых апейроэдра с одинаковым расположением вершин . В первом удалены восьмиугольники и установлена конфигурация вершин 4.4.4.6. Его можно рассматривать как усеченные кубооктаэдры и восьмиугольные призмы, сложенные вместе. Вторые можно рассматривать как дополненные восьмиугольные призмы, конфигурация вершин 4.8.4.8.

4.4.4.6	4.8.4.8

Связанные многогранники

Неоднородные варианты с симметрией [4,3,4] и двумя типами усеченных кубооктаэдров можно удвоить, поместив два типа усеченных кубооктаэдров друг на друга, чтобы получить неоднородные соты с усеченными кубооктаэдрами , восьмиугольными призмами , шестиугольными призмами (как дитригональные трапезопризмы) и два вида кубов (прямоугольные трапеции и их C _2v -симметричные варианты). Ее вершинная фигура представляет собой неправильную треугольную бипирамиду .

Вершинная фигура

Двойная ячейка

Затем эту соту можно чередовать, чтобы получить другую неоднородную соту с курносыми кубами , квадратными антипризмами , октаэдрами (в виде треугольных антипризм) и тремя видами тетраэдров (в виде тетрагональных дисфеноидов, филлических дисфеноидов и неправильных тетраэдров).

Вершинная фигура

Чередованные всеусеченные кубические соты

Чередованные всеусеченные кубические соты
Тип	Выпуклые соты
Символ Шлефли	чт _0,1,2,3 {4,3,4}
Диаграмма Кокстера
Клетки	с{4,3} с{2,4} {3,3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура
Симметрия	[[4,3,4]] ⁺
Двойной	Двойные чередующиеся всеусеченные кубические соты
Характеристики	Вершинно-транзитивный , неоднородный

Перемежающиеся всеусеченные кубические соты или всенаправленные кубические соты могут быть построены путем чередования всеусеченных кубических сот, хотя их нельзя сделать однородными, но можно представить диаграмму Кокстера : и обладает симметрией [[4,3,4]] ⁺. Он делает курносые кубы из усеченных кубооктаэдров , квадратные антипризмы из восьмиугольных призм и создает новые тетраэдрические ячейки из промежутков.

Двойные чередующиеся всеусеченные кубические соты

Двойные чередующиеся всеусеченные кубические соты
Тип	Двойные чередующиеся однородные соты
Символ Шлефли	дхт _0,1,2,3 {4,3,4}
Диаграмма Кокстера
Клетка
Вершинные фигуры	пятиугольный икоситетраэдр тетрагональный трапецоэдр тетраэдр
Симметрия	[[4,3,4]] ⁺
Двойной	Чередованные всеусеченные кубические соты
Характеристики	Клеточно-транзитивный

Двойные чередующиеся всеусеченные кубические соты представляют собой заполняющие пространство соты, построенные как двойные чередующиеся всеусеченные кубические соты .

24 ячейки помещаются вокруг вершины, создавая хирально -октаэдрическую симметрию , которую можно совмещать во всех трех измерениях:

Отдельные клетки обладают 2-кратной вращательной симметрией. В 2D ортогональной проекции это выглядит как зеркальная симметрия.

Представления ячеек
Сеть

Рунчичские скошенные кубические соты

Рунчичские скошенные кубические соты
Тип	Выпуклые соты
Символ Шлефли	ср ₃ {4,3,4}
Диаграммы Кокстера
Клетки	с2 _{ 3,4} с{4,3} {}x{4} {}х{3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура
Группа Коксетера	[4,3 ⁺,4]
Двойной	Клетка:
Характеристики	Вершинно-транзитивный , неоднородный

Рунические скошенные кубические соты или рунические свисающие кубические соты построены путем удаления чередующихся длинных прямоугольников из восьмиугольников и не являются однородными, но их можно представить в виде диаграммы Коксетера. . Он имеет ромбокубооктаэдры (с симметрией T _h ), курносые кубы , два вида кубов : квадратные призмы и прямоугольные трапеции призмы (топологически эквивалентные кубу , но с симметрией D _2d ), а также треугольные призмы (как клинья симметрии C _2v ), заполняющие промежутки. .

Биортоснуб кубические соты

Биортоснуб кубические соты
Тип	Выпуклые соты
Символ Шлефли	2с _0,3 {4,3,4}
Диаграммы Кокстера
Клетки	с2 _{ 3,4} {}x{4}
Лица	треугольник {3} квадрат {4}
Вершинная фигура	( Тетрагональный антиклин )
Группа Коксетера	[[4,3 ⁺,4]]
Двойной	Клетка:
Характеристики	Вершинно-транзитивный , неоднородный

построены Кубические соты биортоснуба путем удаления чередующихся длинных прямоугольников из восьмиугольников ортогонально и не являются однородными, но их можно представить в виде диаграммы Коксетера. . Он имеет ромбокубооктаэдры (с симметрией T _h ) и два вида кубов : квадратные призмы и прямоугольные трапеции призмы (топологически эквивалентные кубу , но с симметрией D _2d ).

Усеченные квадратные призматические соты

Усеченные квадратные призматические соты
Тип	Равномерные соты
Символ Шлефли	t{4,4}×{∞} или t _0,1,3 {4,4,2,∞} tr{4,4}×{∞} или t _0,1,2,3 {4,4,∞}
Диаграмма Кокстера-Динкина
Клетки	{}x{8} {}x{4}
Лица	квадрат {4} восьмиугольник {8}
Группа Коксетера	[4,4,2,∞]
Двойной	Квадратно-призматическая плитка Тетракис Клетка:
Характеристики	Вершинно-транзитивный

Усеченные квадратные призматические соты или томо-квадратные призматические ячейки ( представляют собой замощение или соты ) в евклидовом трехмерном пространстве . Он состоит из восьмиугольных призм и кубов в соотношении 1:1.

Он построен из усеченной квадратной плитки, выдавленной в виде призм.

Это один из 28 выпуклых однородных сот .

Курносые квадратные призматические соты

Курносые квадратные призматические соты
Тип	Равномерные соты
Символ Шлефли	с{4,4}×{∞} ср{4,4}×{∞}
Диаграмма Кокстера-Динкина
Клетки	{}x{4} {}х{3}
Лица	треугольник {3} квадрат {4}
Группа Коксетера	[4 ⁺,4,2,∞] [(4,4) ⁺,2,∞]
Двойной	Каирские пятиугольные призматические соты Клетка:
Характеристики	Вершинно-транзитивный

Курносые квадратные призматические соты или симо-квадратные призматические ячейки ) , заполняющую пространство, представляют собой мозаику (или соты в евклидовом трехмерном пространстве . Он состоит из кубов и треугольных призм в соотношении 1:2.

Он построен из плоской квадратной плитки, выдавленной в виде призм.

Это один из 28 выпуклых однородных сот .

Курносые квадратные антипризматические соты

Курносые квадратные антипризматические соты
Тип	Выпуклые соты
Символ Шлефли	ht _1,2,3 {4,4,2,∞} ht _0,1,2,3 {4,4,∞}
Диаграмма Кокстера-Динкина
Клетки	с{2,4} {3,3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура
Симметрия	[4,4,2,∞] ⁺
Характеристики	Вершинно-транзитивный , неоднородный

Курносые квадратные антипризматические соты можно построить путем чередования усеченных квадратных призматических сот, хотя их нельзя сделать однородными, но можно представить диаграмму Коксетера : и имеет симметрию [4,4,2,∞] ⁺. Он образует квадратные антипризмы из восьмиугольных призм , тетраэдры (как тетрагональные дисфеноиды) из кубов и два тетраэдра из треугольных бипирамид .

См. также

Архитектурно-тектоническая и катоптрическая мозаика
Переменные кубические соты
Список правильных многогранников
Кубические соты порядка 5. Гиперболические кубические соты с 5 кубиками на ребро.
Курносый (геометрия)
Воксель

Ссылки

^ Для перекрестных ссылок им даны списочные индексы Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51). -52, 61-65) и Грюнбаум (1-28).
^ [1] , A000029 6-1 случаев, пропуск одного с нулевыми оценками
^ Уильямс, 1979, стр. 199, рисунок 5-38.
^ кантические курносые кубические соты

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 21, Наименование архимедовых и каталонских многогранников и мозаик, Архитектурные и катоптрические мозаики, стр. 292-298, включает все непризматические формы)
Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 стр. 296, Таблица II: Обычные соты
Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Бранко Грюнбаум , Равномерные разбиения трехмерного пространства. Геомбинаторика 4 (1994), 49–56.
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10] (1.9 Равномерные пространственные заполнения)
А. Андреини , О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях , Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Клитцинг, Ричард. «3D Евклидовы соты x4o3o4o - chon - O1» .
Равномерные соты в трехмерном пространстве: 01-Чон

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] Для перекрестных ссылок им даны списочные индексы Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51). -52, 61-65) и Грюнбаум (1-28).

[2] [1] , A000029 6-1 случаев, пропуск одного с нулевыми оценками

[3] Уильямс, 1979, стр. 199, рисунок 5-38.

[4] кантические курносые кубические соты

[1]

[2]

[3]

[4]