Плоская квадратная плитка

Плоская квадратная плитка

Тип	Полурегулярная черепица
Конфигурация вершин	3.3.4.3.4
Символ Шлефли	с{4,4} ср{4,4} или $s{\begin{Bmatrix}4\\4\end{Bmatrix}}$
Символ Витхоффа	\| 4 4 2
Диаграмма Кокстера	или
Симметрия	p4g , [4 ⁺,4], (4*2)
Симметрия вращения	р4 , [4,4] ⁺, (442)
Аббревиатура Бауэрса	Снаскват
Двойной	Каирская пятиугольная плитка
Характеристики	Вершинно-транзитивный

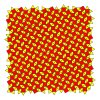
В геометрии представляет плосконосая квадратная мозаика собой полуправильную мозаику евклидовой плоскости . находятся три треугольника и два квадрата В каждой вершине . Его символ Шлефли — s{4,4} .

Конвей называет ее курносой кадрилью , построенной с помощью операции курносости , примененной к квадратной мозаике (кадриль).

3 правильных и 8 полуправильных мозаик На плоскости .

Равномерные раскраски

имеет две различные однородные окраски Курносая квадратная плитка . (Наименование цветов по индексам вокруг вершины (3.3.4.3.4): 11212, 11213.)

Раскраска	11212	11213
Симметрия	4*2, [4 ⁺,4], (p4g)	442, [4,4] ⁺, (п4)
Символ Шлефли	с{4,4}	ср{4,4}
Символ Витхоффа		\| 4 4 2
Диаграмма Кокстера

Упаковка круга

Плоскую квадратную плитку можно использовать в качестве упаковки кругов , размещая круги одинакового диаметра в центре каждой точки. Каждый круг соприкасается с пятью другими кругами упаковки ( число поцелуя ). ^[1]

Строительство Витхоффа

Плоско -квадратная мозаика может быть построена как усечения операция квадратной мозаики или как альтернативное усечение из усеченной квадратной мозаики .

Альтернативное усечение удаляет все остальные вершины, создавая новые треугольные грани в удаленных вершинах, и уменьшает исходные грани до половины количества сторон. В этом случае, начиная с замощения усеченных квадратов с 2 восьмиугольниками и 1 квадратом на вершину, грани восьмиугольника превращаются в квадраты, а грани квадрата вырождаются в ребра, и в усеченных вершинах вокруг исходного квадрата появляются 2 новых треугольника.

Если исходная мозаика состоит из правильных граней, новые треугольники будут равнобедренными. Начиная с восьмиугольников с чередующимися длинными и короткими ребрами, полученными из правильного двенадцатиугольника , получится курносая плитка с идеальными равносторонними треугольными гранями.

Пример:

Правильные восьмиугольники поочередно усекаются	→ (Альтернативный усечение)	Равнобедренные треугольники (неравномерная мозаика)
Неправильные восьмиугольники поочередно усекаются	→ (Альтернативный усечение)	Равносторонние треугольники

Связанные мозаики

Дважды примененный к квадратному мозаике оператор snub , хотя он и не имеет правильных граней, состоит из квадрата с неправильными треугольниками и пятиугольниками.
Родственная изогональная мозаика , объединяющая пары треугольников в ромбы.
2-изогональную мозаику можно составить, объединив 2 квадрата и 3 треугольника в семиугольники.
двойственна Пятиугольная плитка Каира курносой квадратной плитке.

Связанные k-равномерные мозаики

Эта мозаика связана с вытянутой треугольной мозаикой , которая также имеет 3 треугольника и два квадрата в вершине, но в другом порядке: 3.3.3.4.4. Две вершинные фигуры можно смешивать во многих k -однородных мозаиках . ^[2]^[3]

Связанные мозаики треугольников и квадратов
курносый квадрат	удлиненный треугольный	2-униформа		3-униформа
п4г, (4*2)	п2, (2222)	п2, (2222)	см, (2*22)	п2, (2222)
[3 ²434]	[3 ³4 ²]	[3 ³4 ²; 3 ²434]	[3 ³4 ²; 3 ²434]	[2: 3 ³4 ²; 3 ²434]	[3 ³4 ²; 2: 3 ²434]

Связанные топологические серии многогранников и мозаики

Плоско -квадратная мозаика является третьей в ряду курносых многогранников и мозаик с фигурой вершины 3.3.4.3. н .

4 n 2 мутации симметрии курносых мозаик: 3.3.4.3.n v т и
Symmetry 4n2	Spherical		Euclidean	Compact hyperbolic				Paracomp.
Symmetry 4n2	242	342	442	542	642	742	842	∞42
Snub figures
Config.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Gyro figures
Config.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Плоско -квадратная мозаика является третьей в ряду курносых многогранников и мозаик с фигурой вершины 3.3. п .3. н .

4 n 2 мутации симметрии курносых мозаик: 3.3.n.3.n
Symmetry 4n2	Spherical		Euclidean	Compact hyperbolic				Paracompact
Symmetry 4n2	222	322	442	552	662	772	882	∞∞2
Snub figures
Config.	3.3.2.3.2	3.3.3.3.3	3.3.4.3.4	3.3.5.3.5	3.3.6.3.6	3.3.7.3.7	3.3.8.3.8	3.3.∞.3.∞
Gyro figures
Config.	V3.3.2.3.2	V3.3.3.3.3	V3.3.4.3.4	V3.3.5.3.5	V3.3.6.3.6	V3.3.7.3.7	V3.3.8.3.8	V3.3.∞.3.∞

Равномерные мозаики, основанные на симметрии квадратных мозаик v т и
Symmetry: [4,4], (*442)							[4,4]⁺, (442)	[4,4⁺], (4*2)


{4,4}	t{4,4}	r{4,4}	t{4,4}	{4,4}	rr{4,4}	tr{4,4}	sr{4,4}	s{4,4}
Uniform duals


V4.4.4.4	V4.8.8	V4.4.4.4	V4.8.8	V4.4.4.4	V4.4.4.4	V4.8.8	V3.3.4.3.4

См. также

Ссылки

^ Порядок в пространстве: справочник по дизайну, Кейт Кричлоу, стр.74-75, образец круга C.
^ Чави, Д. (1989). «Замощения правильными многоугольниками - II: Каталог мозаик» . Компьютеры и математика с приложениями . 17 : 147–165. дои : 10.1016/0898-1221(89)90156-9 .
^ «Единые плитки» . Архивировано из оригинала 9 сентября 2006 г. Проверено 9 сентября 2006 г.

Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]
Клитцинг, Ричард. «2D евклидовы мозаики s4s4s — snasquat — O10» .
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . (Глава 2.1: Правильные и однородные мозаики , стр. 58-65)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . стр.38
Дейл Сеймур и Джилл Бриттон , «Введение в тесселяцию» , 1989 г., ISBN 978-0866514613 , стр. 50–56, двойной стр. 115

Внешние ссылки

Вайсштейн, Эрик В. «Полурегулярная мозаика» . Математический мир .

[Critchlow-1] Порядок в пространстве: справочник по дизайну, Кейт Кричлоу, стр.74-75, образец круга C.

[2] Чави, Д. (1989). «Замощения правильными многоугольниками - II: Каталог мозаик» . Компьютеры и математика с приложениями . 17 : 147–165. дои : 10.1016/0898-1221(89)90156-9 .

[3] «Единые плитки» . Архивировано из оригинала 9 сентября 2006 г. Проверено 9 сентября 2006 г.

[1]

[2]

[3]