Равномерные соты

В геометрии , однородные соты или равномерная тесселяция бесконечный однородный многогранник — это вершинно-транзитивные соты , состоящие из однородных граней многогранника . Все его вершины одинаковы, и в каждой вершине одинаковое сочетание и расположение граней. Его размерность можно уточнить как $n$ -сот для $n$ -мерных сот.

n $-$ мерные однородные соты можно построить на поверхности $n$ -сфер, в $n$ -мерном евклидовом пространстве и $n$ -мерном гиперболическом пространстве . Двумерные однородные соты чаще называют равномерным мозаикой или однородной мозаикой.

Почти все однородные мозаики могут быть созданы с помощью конструкции Витхоффа и представлены диаграммой Коксетера-Динкина . Терминология для выпуклых однородных многогранников, используемая в однородных многогранниках , однородных 4-многогранниках , однородных 5-многогранниках , однородных 6-многогранниках , однородных мозаиках и выпуклых однородных сотовых изделиях, была придумана Норманом Джонсоном .

Витоффова мозаика может быть определена фигурой вершины . Для двумерных мозаик они могут быть заданы конфигурацией вершин, в которой перечислена последовательность граней вокруг каждой вершины. Например, $4.4.4.4$ представляет собой обычную мозаику, квадратную мозаику с 4 квадратами вокруг каждой вершины. В общем, $n$ -мерные фигуры вершин однородной тесселяции определяются $(n -1)$ -многогранником с ребрами, помеченными целыми числами, представляющими количество сторон многоугольной грани на каждом ребре, исходящем из вершины.

Примеры однородных сот

2-мерные мозаики
	сферический	евклидов	гиперболический
	Основная статья: Однородный многогранник	Основная статья: Список однородных мозаик	Основная статья: Равномерные мозаики в гиперболической плоскости
Диаграмма Кокстера
Картина	Усеченный икосододекаэдр	Усеченная трехгексагональная мозаика	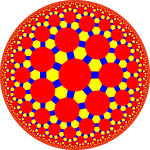Усеченная трехгептагональная мозаика ( модель диска Пуанкаре )	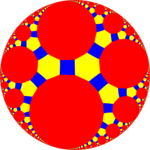Усеченная триапейрогональная мозаика
Вершинная фигура
3-мерные соты
	3-сферический	3-евклидово	3-гиперболический
	Основная статья: Равномерный полихорон	Основная статья: Выпуклые однородные соты	Основная статья: Однородные соты в гиперболическом пространстве и паракомпактные однородные соты
Диаграмма Кокстера
Картина	( Стереографическая проекция ) 16-ячеечный	кубические соты	Додекаэдрические соты порядка 4 ( модель Бельтрами – Клейна )	шестиугольная сотовая плитка порядка 4 ( модель диска Пуанкаре )
Вершинная фигура	( Октаэдр )	(Октаэдр)	(Октаэдр)	(Октаэдр)

См. также

Ссылки

Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Бранко Грюнбаум , Равномерные разбиения трехмерного пространства. Геомбинаторика 4 (1994), 49–56.
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х .
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . WH Фриман и компания. ISBN 0-7167-1193-1 .
HSM Coxeter , Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
Кричлоу, Кейт (1970). Порядок в космосе: справочник по дизайну . Викинг Пресс. ISBN 0-500-34033-1 .
Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
А. Андреини , О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях , Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.

Внешние ссылки

Вайсштейн, Эрик В. «Равномерная мозаика» . Математический мир .
Мозаика плоскости
Клитцинг, Ричард. «2D евклидовы мозаики» .