Каирская пятиугольная плитка
| Каирская пятиугольная плитка | |
|---|---|
 Равносторонняя форма каирской мозаики | |
| Тип | Пятиугольная плитка |
| Лица | неправильный пятиугольник |
| Двойной многогранник | Плоская квадратная плитка |
| Характеристики | лице-переходный |
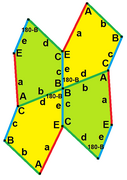
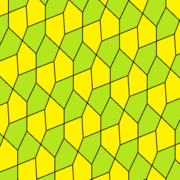
В геометрии каирская пятиугольная плитка представляет собой мозаику евклидовой плоскости конгруэнтными выпуклыми пятиугольниками , образованную путем наложения двух мозаик плоскости шестиугольниками и названную в честь ее использования в качестве дизайна мощения в Каире . Ее еще называют сетью Мак-Магона. [1] после Перси Александра МакМагона , который изобразил это в своей публикации 1921 года « Новые математические игры» . [2] Джон Хортон Конвей назвал это 4-кратной пентильей . [3]
Бесконечно много различных пятиугольников могут образовывать этот узор, принадлежащих к двум из 15 семейств выпуклых пятиугольников, которые могут замостить плоскость . Их мозаики имеют разную симметрию; все лица симметричны. Одна конкретная форма мозаики, двойственная плосконосой квадратной мозаике , имеет плитки с минимально возможным периметром среди всех пятиугольных плиток. Другая форма, накладывающая на две сплющенные мозаики правильные шестиугольники, используется в Каире и обладает тем свойством, что каждое ребро коллинеарно бесконечному множеству других ребер.
В архитектуре за пределами Каира каирская плитка использовалась в архитектуре Великих Моголов начала 20-го века в Индии 18-го века, в Лаайсхалле в Германии, а также во многих современных зданиях и сооружениях. Он также был изучен как кристаллическая структура и появляется в искусстве Эшера .
Структура и классификация
[ редактировать ]Объединение всех ребер каирского разбиения аналогично объединению двух разбиений плоскости шестиугольниками . Каждый шестиугольник одной мозаики окружает две вершины другой мозаики и делится шестиугольниками другой мозаики на четыре пятиугольника в мозаике Каира. [4] Бесконечно много разных пятиугольников могут образовывать каирские мозаики, все с одинаковым рисунком примыкания плиток и с одинаковым разложением на шестиугольники, но с разной длиной ребер, углами и симметрией. Пятиугольники, образующие эти мозаики, можно сгруппировать в два разных бесконечных семейства, взятых из 15 семейств выпуклых пятиугольников, которыми можно замостить плоскость . [5] и пять семейств пятиугольников, обнаруженных Карлом Рейнхардтом в 1918 году, которые могут замостить плоскость изоэдрально (все плитки симметричны друг другу). [6]
Одно из этих двух семейств состоит из пятиугольников, имеющих два несмежных прямых угла , причем под каждым из этих прямых углов сходятся пары сторон одинаковой длины. Любой пятиугольник, отвечающий этим требованиям, замостит плоскость копиями, которые в выбранных прямых углах повернуты на прямой угол относительно друг друга. На сторонах пятиугольника, не примыкающих ни к одному из этих двух прямых углов, встречаются две плитки, повернутые на угол 180° относительно друг друга. В результате получается изоэдральная мозаика, а это означает, что любой пятиугольник в мозаике может быть преобразован в любой другой пятиугольник за счет симметрии мозаики. Эти пятиугольники и их мозаика часто относят к «типу 4» в списке типов пятиугольников, которые могут располагаться плиткой. [4] Для любой мозаики Каира типа 4 двенадцать одинаковых плиток также могут покрывать поверхность куба, при этом одна плитка согнута поперек каждого края куба и три прямых угла плитки встречаются в каждой вершине куба, образуя ту же комбинаторную структуру, что и обычная мозаика. додекаэдр . [7] [8]
Другое семейство пятиугольников, образующих мозаику Каира, - это пятиугольники, которые имеют два дополнительных угла в несмежных вершинах, каждый из которых имеет одинаковые длины двух инцидентных ему сторон. В их мозаиках вершины с дополнительными углами чередуются вокруг каждой вершины четвертой степени. Пятиугольники, отвечающие этим ограничениямобычно не входят в число 15 семейств пятиугольников, выложенных плиткой; скорее, они являются частью более крупного семейства пятиугольников (пятиугольники «типа 2»), которые по-другому закрывают плоскость изоэдра. [4]
Двусторонне-симметричные каирские мозаики образованы пятиугольниками, принадлежащими семействам как 2-го, так и 4-го типа. [4] Кирпичный узор мощения корзинчатого плетения можно рассматривать как вырожденный случай двусторонне-симметричной каирской плитки, где каждый кирпич ( прямоугольник) интерпретируется как пятиугольник с четырьмя прямыми углами и одним углом 180°. [9]
- Плитки Cairo типа 2 имеют несмежные дополнительные углы с одинаковыми длинами двух соседних сторон.
- Плитки типа 4 имеют несмежные прямые углы между парами сторон одинаковой длины.
- В двусторонне-симметричных мозаиках (принадлежащих к обоим типам) используются плитки с несмежными прямыми углами и четырьмя равными ребрами.
- Каирская плитка типа 2, цветом показаны отраженные и неотраженные плитки.
- В мозаике Каира типа 4 пятиугольники могут быть двусторонне симметричными, даже если мозаика не
- Корзинчатое переплетение, вырожденная двусторонне-симметричная мозаика, с наложенной невырожденной мозаикой.
можно присвоить шестимерные полуцелые Пятиугольникам мозаики координаты таким образом, чтобы количество шагов от края до края между любыми двумя пятиугольниками равнялось L 1 расстояние между их координатами. Шесть координат каждого пятиугольника можно сгруппировать в две тройки координат, в которых каждая тройка дает координаты шестиугольника в аналогичной трехмерной системе координат для каждой из двух наложенных мозаик шестиугольника. [10] Количество плиток, которые шагов от любой плитки, для , задается координационной последовательностью в котором после первых трех членов каждый член отличается на 16 от члена на три шага назад в последовательности. Можно также определить аналогичные координационные последовательности для вершин замощения, а не для его плиток, но поскольку существует два типа вершин (третьей и четвертой степени), то таким образом возникают две разные координационные последовательности. Последовательность четвертой степени такая же, как и для квадратной сетки . [11] [12]
Особые случаи
[ редактировать ]Каталонская черепица
[ редактировать ]Плосконосая квадратная мозаика , состоящая из двух квадратов и трех равносторонних треугольников вокруг каждой вершины, имеет двусторонне-симметричную каирскую мозаику в качестве двойной мозаики . [13] Каирскую мозаику можно сформировать из курносой квадратной мозаики, поместив вершину каирской мозаики в центр каждого квадрата или треугольника курносой квадратной мозаики и соединив эти вершины ребрами, когда они исходят из соседних плиток. [14] Его пятиугольники можно описать вокруг круга . Они имеют четыре длинных края и один короткий, длины которых находятся в соотношении . Углы этих пятиугольников образуют последовательность 120°, 120°, 90°, 120°, 90°. [15]
Плосконосая квадратная плитка является архимедовой плиткой , а как двойственная архимедовой плитке эта форма каирской пятиугольной плитки является каталонской плиткой или плиткой Лавеса. [14] Это одна из двух моноэдральных пятиугольных плиток, которые, когда плитки имеют единичную площадь, минимизируют периметр плиток. Другой также представляет собой мозаику из описанных пятиугольников с двумя прямыми углами и тремя углами по 120 °, но с двумя прямыми углами, примыкающими друг к другу; существует также бесконечно много мозаик, образованных объединением обоих видов пятиугольников. [15]
Плитки с коллинеарными краями
[ редактировать ]
Пятиугольники с целочисленными координатами вершин , , и , с четырьмя равными сторонами короче оставшейся стороны, образует каирскую мозаику, две шестиугольные мозаики которой можно образовать путем сплющивания двух перпендикулярных мозаик правильными шестиугольниками в перпендикулярных направлениях в соотношении . Эта форма каирской мозаики наследует свойство мозаики правильных шестиугольников (не изменяющееся при уплощении), что каждое ребро коллинеарно бесконечному множеству других ребер. [9] [16]
Плитки с равными длинами сторон
[ редактировать ]Правильный пятиугольник не может образовывать мозаику Каира, так как он не замощает плоскость без пробелов. Существует уникальный равносторонний пятиугольник , который может образовывать каирскую мозаику 4-го типа; у него пять равных сторон, но углы неравны, а мозаика двусторонне симметрична. [4] [13] Бесконечно много других равносторонних пятиугольников могут образовывать каирские мозаики 2-го типа. [4]
Приложения
[ редактировать ]Несколько улиц в Каире вымощены коллинеарной каирской плиткой; [9] [17] это приложение является источником названия мозаики. [18] [19] По состоянию на 2019 год этот узор все еще можно рассматривать как украшение поверхности квадратной плитки возле моста Каср-эль-Нил и станции метро El Behoos ; другие версии плитки можно увидеть и в других частях города. [20] Некоторые авторы, в том числе Мартин Гарднер, писали, что этот узор более широко используется в исламской архитектуре , и хотя это утверждение, по-видимому, было основано на недоразумении, узоры, напоминающие каирскую плитку, видны на гробнице Итимад-уда 17-го века. - Даула в Индии, а сама каирская плитка была найдена на Великих Моголов Джали 17-го века . [16]
- Гробница Итимад-уд-Даулы с прямоугольными боковыми панелями, напоминающими каирскую плитку.
- Centar Zamet , на стенах которого видна каирская плитка.
- Каирская плитка в Хёрсхольме , Дания
Одна из самых ранних публикаций о каирской плитке как декоративном узоре встречается в книге по текстильному дизайну 1906 года. [21] Изобретатель Х.К. Мур подал в США патент на плитку, образующую этот узор, в 1908 году. [22] Примерно в то же время Villeroy & Boch создала линию керамической напольной плитки с рисунком каирской плитки, которая использовалась в фойе Laeiszhalle в Гамбурге , Германия. Каирская плитка использовалась в качестве декоративного рисунка во многих недавних архитектурных проектах; например, центр города Хёрсхольм в Дании выложен этим узором, а спортивный зал Centar Zamet в Хорватии использует его как для наружных стен, так и для тротуарной плитки. [16]
В кристаллографии это разбиение изучается как минимум с 1911 года. [23] Он был предложен в качестве структуры слоистых кристаллов гидратов . [24] некоторые соединения висмута и железа , [25] и пента-графен , гипотетическое соединение чистого углерода . В пентаграфеновой структуре ребра тайлинга, инцидентные вершинам четвертой степени, образуют одинарные связи , а остальные ребра образуют двойные связи . В гидрированной форме пентаграфана все связи являются одинарными, а атомы углерода в вершинах структуры третьей степени имеют четвертую связь, соединяющую их с атомами водорода. [26]
Каирскую плитку называют одним из «любимых геометрических узоров» Эшера . [7] Он использовал его в качестве основы для своего рисунка «Ракушки и морские звезды» (1941), в сегменте «Пчелы на цветах» своей «Метаморфозы III» (1967–1968) и в нескольких других рисунках 1967–1968 годов. Изображение этой мозаики также использовалось в качестве обложки первого издания Х. С. М. Коксетера книги «Регулярные комплексные многогранники» в 1974 году . [4] [16]
Ссылки
[ редактировать ]- ^ О'Киф, М.; Хайд, Б.Г. (1980), «Плоские сети в кристаллохимии», «Философские труды Лондонского королевского общества». Серия A, Математические и физические науки , 295 (1417): 553–618, Bibcode : 1980RSPTA.295..553O , doi : 10.1098/rsta.1980.0150 , JSTOR 36648 , S2CID 121456259 .
- ^ Макмахон, майор П.А. (1921), Новые математические игры , University Press, стр. 101
- ^ Конвей, Джон Х .; Бургель, Хайди; Гудман-Штраус, Хаим (2008), Симметрии вещей , А. К. Петерс, с. 288 , ISBN 978-1-56881-220-5
- ^ Jump up to: Перейти обратно: а б с д и ж г Шаттшнайдер, Дорис (1978), «Разбиение плоскости равными пятиугольниками» , журнал Mathematics Magazine , 51 (1): 29–44, doi : 10.1080/0025570X.1978.11976672 , JSTOR 2689644 , MR 0493766
- ^ Рао, Микаэль (2017), Исчерпывающий поиск выпуклых пятиугольников, покрывающих плоскость (PDF) , arXiv : 1708.00274
- ^ Рейнхардт, Карл (1918), О разложении плоскости на многоугольники (Докторская диссертация) (на немецком языке), Борна-Лейпциг: Печать Роберта Носке, «Четвертый тип», с. 78 и рис. 24, с. 81
- ^ Jump up to: Перейти обратно: а б Шатшнайдер, Дорис ; Уокер, Уоллес (1977), «Додекаэдр», MC Escher Kaleidocycles , Ballantine Books, стр. 22 ; перепечатано Ташеном, 2015 г.
- ^ Томас, Б.Г.; Ханн, Массачусетс (2008), «Узор с помощью проекции: замощение додекаэдра и других твердых тел» , в Сарханги, Реза; Секин, Карло Х. (ред.), Бриджес Леуварден: математика, музыка, искусство, архитектура, культура , Лондон: Tarquin Publications, стр. 101–108, ISBN 9780966520194
- ^ Jump up to: Перейти обратно: а б с Макмиллан, Р.Х. (декабрь 1979 г.), «Пирамиды и тротуары: некоторые мысли из Каира», The Mathematical Gazette , 63 (426): 251–255, doi : 10.2307/3618038 , JSTOR 3618038 , S2CID 125608794
- ^ Ковач, Гергеи; Надь, Бенедек; Тургай, Нешет Дениз (май 2021 г.), «Расстояние по каирскому образцу», Письма о распознавании образов , 145 : 141–146, Бибкод : 2021PaReL.145..141K , doi : 10.1016/j.patrec.2021.02.002 , S2CID 233375125
- ^ Координационные последовательности для пятиугольной мозаики Каира в Онлайн-энциклопедии целочисленных последовательностей : A219529 для пятиугольников, A296368 для вершин третьей степени и A008574 для вершин четвертой степени, получено 17 июня 2021 г.
- ^ Гудман-Штраус, К.; Sloane, NJA (2019), «Подход к раскраски к поиску координационных последовательностей» (PDF) , Acta Crystallographica Раздел A , 75 (1): 121–134, ARXIV : 1803.08530 , DOI : 10.1107/S2053273318014481 , MR 3896412 , PMID . 30575590 , S2CID 4553572 , заархивировано из оригинала (PDF) 17 февраля 2022 г. , получено 18 июня 2021 г.
- ^ Jump up to: Перейти обратно: а б Роллетт, AP (сентябрь 1955 г.), «2530. Пятиугольная мозаика», Mathematical Notes, The Mathematical Gazette , 39 (329): 209, doi : 10.2307/3608750 , JSTOR 3608750 , S2CID 250439435
- ^ Jump up to: Перейти обратно: а б Штойрер, Вальтер; Джемучадзе, Юлия (2016), Интерметаллиды: структуры, свойства и статистика , Монографии Международного союза кристаллографов по кристаллографии, том. 26, Издательство Оксфордского университета, с. 42, ISBN 9780191023927
- ^ Jump up to: Перейти обратно: а б Чунг, Пинг Нгай; Фернандес, Мигель А.; Ли, Ифэй; Мара, Майкл; Морган, Фрэнк ; Плата, Исамар Роза; Шах, Нирали; Виейра, Луис Сордо; Викнер, Елена (2012), «Изопериметрические пятиугольные мозаики», Уведомления Американского математического общества , 59 (5): 632–640, doi : 10.1090/noti838 , MR 2954290
- ^ Jump up to: Перейти обратно: а б с д Бейли, Дэвид, «Каирская плитка» , «Мир мозаики в стиле Эшера» Дэвида Бейли , получено 6 декабря 2020 г.
- ^ Данн, Дж. А. (декабрь 1971 г.), «Тесселяции пятиугольниками», The Mathematical Gazette , 55 (394): 366–369, doi : 10.2307/3612359 , JSTOR 3612359 , S2CID 118680100 . Хотя Данн пишет, что в Каире использовалась равносторонняя форма мозаики, это представляется ошибкой.
- ^ Альсина, Клауди; Нельсен, Роджер Б. (2010), Очаровательные доказательства: путешествие в изящную математику , Математические пояснения Дольчиани, том. 42, Математическая ассоциация Америки, с. 164, ISBN 978-0-88385-348-1 .
- ^ Мартин, Джордж Эдвард (1982), Геометрия преобразований: введение в симметрию , Тексты для студентов по математике , Springer, стр. 119, ISBN 978-0-387-90636-2 .
- ^ Морган, Фрэнк (2019), «Моя секретная миссия по поиску каирских мозаик», The Mathematical Intelligencer , 41 (3): 19–22, doi : 10.1007/s00283-019-09906-7 , MR 3995312 , S2CID 198468426
- ^ Нисбет, Гарри (1906), Грамматика текстильного дизайна , Лондон: Скотт, Гринвуд и сын, стр. 101
- ^ Мур, ХК (20 июля 1909 г.), Плитка (патент США 928 320).
- ^ Хааг, Ф. (1911), «Деления регулярного плана», Журнал кристаллографии, кристаллической геометрии, физики кристаллов, кристаллохимии , 49 : 360–369, hdl : 2027/uc1.b3327994. См., в частности, рисунки 2b, стр. 361 и 4а, с. 363.
- ^ Банару, AM; Банару, Г.А. (август 2011 г.), «Каирское разбиение и топология слоистых гидратов», Вестник химии Московского университета , 66 (3), статья 159, doi : 10.3103/S0027131411030023 , S2CID 96002269
- ^ Рессуш, Э.; Симонет, В.; Каналс, Б.; Господинов М.; Скумриев, В. (декабрь 2009 г.), «Магнитное расстройство в каирской пятиугольной решетке на основе железа» , Physical Review Letters , 103 (26): 267204, arXiv : 1001.0710 , Bibcode : 2009PhRvL.103z7204R , doi : 10.1103/physrevlett. 103.267204 , PMID 20366341 , S2CID 20752605
- ^ Чжан, Шуньхун; Чжоу, Цзянь; Ван, Цянь; Чен, Сяошуан; Кавазоэ, Ёсиюки; Йена, Пуру (февраль 2015 г.), «Пентаграфен: новый аллотроп углерода», Proceedings of the National Academy of Sciences of the United States of America , 112 (8): 2372–2377, Bibcode : 2015PNAS..112.2372Z , doi : 10.1073/pnas.1416591112 , PMC 4345574 , PMID 25646451