Список изотоксальных многогранников и мозаик
В геометрии . изотоксальные многогранники и мозаики определяются тем свойством, что они обладают симметрией, переводящей любое ребро в любое другое ребро [1] Многогранники с этим свойством также можно назвать «реберно-транзитивными», но их следует отличать от реберно-транзитивных графов , где симметрии являются комбинаторными, а не геометрическими.
Правильные многогранники бывают изоэдральными (переходными по граням), изогональными (переходными по вершинам) и изотоксальными (переходными по ребрам).
Квазиправильные многогранники изогональны и изотоксальны, но не изоэдральны; их двойники изоэдральны и изотоксалы, но не изогональны.
Двойник изотоксального многогранника также является изотоксальным многогранником. (См. статью Двойной многогранник .)
Выпуклые изотоксальные многогранники
[ редактировать ]Двойственный выпуклому многограннику также является выпуклым многогранником. [2]
Существует девять выпуклых изотоксальных многогранников, основанных на Платоновых телах : пять (правильных) Платоновых тел, два ( квазирегулярных ) общих ядра двойственных Платоновых тел и два их двойственных тела.
Вершинными фигурами квазиправильных форм являются (квадраты или) прямоугольники; вершинными фигурами двойственных квазиправильных форм являются (равносторонние треугольники и равносторонние треугольники, или) равносторонние треугольники и квадраты, или равносторонние треугольники и правильные пятиугольники.
| Форма | Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный двойной |
|---|---|---|---|---|
| Символ Витхоффа | д | 2 р | р | 2 кв. | 2 | пк | |
| Конфигурация вершин | п д | д п | pqpq | |
| р=3 д=3 |  Тетраэдр {3,3} 3 | 2 3 |  Тетраэдр {3,3} 3 | 2 3 |  Тетратетраэдр ( Октаэдр ) 2 | 3 3 |  Куб (Ромбический шестигранник) |
| р=4 д=3 |  Куб {4,3} 3 | 2 4 |  Октаэдр {3,4} 4 | 2 3 |  Кубооктаэдр 2 | 3 4 |  Ромбический додекаэдр |
| р=5 д=3 |  Додекаэдр {5,3} 3 | 2 5 |  Икосаэдр {3,5} 5 | 2 3 |  Икосододекаэдр 2 | 3 5 |  Ромбический триаконтаэдр |
Изотоксальные звездчатые многогранники
[ редактировать ]Двойственный невыпуклому многограннику также является невыпуклым многогранником. [2] (По контрасту.)
Существует десять невыпуклых изотоксальных многогранников, основанных на квазиправильном октаэдре, кубооктаэдре и икосододекаэдре: пять (квазиправильных) полумногогранников, основанных на квазиправильном октаэдре, кубооктаэдре и икосододекаэдре, а также их пять (бесконечных) двойников:
| Форма | Квазирегулярный | Квазирегулярный двойной |
|---|---|---|
| р=3 д=3 |   Тетрагемишестиэдр |  Тетрагемигексакрон |
| р=4 д=3 |   Кубогемиоктаэдр |  Гексагемиоктакрон |
  Октагемиоктаэдр |  Октагемиоктакрон (визуально неотличим от гексагемиоктакрона) (*) | |
| р=5 д=3 |   Малый икосихемидодекаэдр |  Маленький икосихемидодекакрон (визуально неотличимый от малого додекахемидодекакрона) (*) |
  Малый додекахемидодекаэдр |  Малый додекахемидодекакрон |
(*) Грани, ребра и точки пересечения одинаковы; только некоторые другие из этих точек пересечения, не находящиеся на бесконечности, считаются вершинами.
Существует шестнадцать невыпуклых изотоксальных многогранников, основанных на многогранниках Кеплера-Пуансо : четыре (правильных) многогранника Кеплера-Пуансо, шесть ( квазирегулярных ) общих ядер двойственных многогранников Кеплера-Пуансо (включая четыре полуполиэдра) и их шесть двойников ( включая четыре (бесконечные) полуполиэдра-двойника):
| Форма | Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный двойной |
|---|---|---|---|---|
| Символ Витхоффа | д | 2 р | р | 2 кв. | 2 | пк | |
| Конфигурация вершин | п д | д п | pqpq | |
| р=5/2 д=3 |   Большой звездчатый додекаэдр { 5 / 2 ,3}
|   Большой икосаэдр {3, 5 / 2 }
|   Большой икосододекаэдр 2 | 3 5/2 |  Большой ромбический триаконтаэдр |
  Большой икосихемидодекаэдр |  Большой икосихемидодекакрон | |||
  Большой додекахемидодекаэдр |  Большой додекахемидодекакрон | |||
| р=5/2 д=5 |   Малый звездчатый додекаэдр { 5 / 2 ,5}
|   Большой додекаэдр {5, 5 / 2 }
|   Додекадодекаэдр 2 | 5 5/2 |  Медиальный ромбический триаконтаэдр |
  Малый икосихемидодекаэдр |  Малый додекегемикосакрон | |||
  Большой додекахемидодекаэдр |  Большой додекегемикосакрон |
Наконец, есть шесть других невыпуклых изотоксальных многогранников: три квазиправильных дитригональных (3 | pq) звездчатых многогранника и три двойственных им:
| Квазирегулярный | Квазирегулярный двойной |
|---|---|
| 3 | пк | |
  Большой дитригональный икосододекаэдр 3/2 | 3 5 |  Большой триамбический икосаэдр |
  Дитригональный додекадодекаэдр 3 | 5/3 5 |  Медиальный триамбический икосаэдр |
  Малый дитригональный икосододекаэдр 3 | 5/2 3 |  Малый триамбический икосаэдр |
Изотоксальные мозаики евклидовой плоскости
[ редактировать ]Существует как минимум 5 многоугольных мозаик евклидовой плоскости, которые являются изотоксальными. (Дуальная квадратная мозаика воссоздает себя во всех четырех формах.)
| Обычный | Двойной обычный | Квазирегулярный | Квазирегулярный двойной |
|---|---|---|---|
 Шестиугольная плитка {6,3} 6 | 2 3 |  Треугольная плитка {3,6} 3 | 2 3 |  Трехгексагональная плитка 2 | 3 6 |  Ромбическая плитка |
 Квадратная плитка {4,4} 4 | 2 4 |  Квадратная плитка {4,4} 2 | 4 4 |  Квадратная плитка {4,4} 4 | 2 4 |  Квадратная плитка {4,4} |
Изотоксальные мозаики гиперболической плоскости
[ редактировать ]Существует бесконечно много изотоксальных многоугольных мозаик гиперболической плоскости, включая конструкции Витгофа из правильных гиперболических мозаик {p,q} и неправых (pqr) групп.
Вот шесть (pq 2) семейств, каждое с двумя правильными формами и одной квазирегулярной формой. Все они имеют ромбические двойники квазирегулярной формы, но показан только один:
| [п, д] | {п, д} | {д, р} | г {р, q} | Двойной r{p,q} |
|---|---|---|---|---|
| Коксетер-Дынкин | ||||
| [7,3] |  {7,3} |  {3,7} |  г{7,3} | 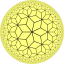 |
| [8,3] |  {8,3} |  {3,8} |  г{8,3} |  |
| [5,4] |  {5,4} |  {4,5} |  г{5,4} |  |
| [6,4] |  {6,4} |  {4,6} |  г{6,4} |  |
| [8,4] |  {8,4} |  {4,8} |  г{8,3} |  |
| [5,5] |  {5,5} |  {5,5} |  г{5,5} |  |
Вот 3 примера семейства (pqr), каждое из которых имеет 3 квазирегулярные формы. Двойники не показаны, но имеют изотоксальные шестиугольные и восьмиугольные грани.
| Коксетер-Дынкин | |||
|---|---|---|---|
| (4 3 3) |  3 | 4 3 |  3 | 4 3 |  4 | 3 3 |
| (4 4 3) |  4 | 4 3 |  3 | 4 4 |  4 | 4 3 |
| (4 4 4) |  4 | 4 4 |  4 | 4 4 |  4 | 4 4 |
Изотоксальные мозаики сферы
[ редактировать ]Все перечисленные выше изотоксальные многогранники можно составить как изотоксальные замощения сферы.
Помимо сферических мозаик, есть еще два семейства, вырождающихся в многогранники. Даже упорядоченный осоэдр может быть полуправильным , с чередующимися двумя лунками и, таким образом, изотоксальным:
- осоэдр {2,q}
- двугранник {p,2}
Ссылки
[ редактировать ]- ^ Питер Р. Кромвель, Многогранники , Издательство Кембриджского университета, 1997, ISBN 0-521-55432-2 , с. 371
- ^ Jump up to: а б «двойственность» . maths.ac-noumea.nc . Проверено 01 октября 2020 г.
- Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . (6.4 Изотоксальные мозаики, 309–321)
- Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Серия A. Математические и физические науки , 246 (916): 401–450, doi : 10.1098/rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446 , S2CID 202575183

