Большой триамбический икосаэдр
| Большой триамбический икосаэдр | Медиальный триамбический икосаэдр | |
 |  | |
| Типы | Двойные однородные многогранники | |
| Группа симметрии | I h | |
| Имя | Большой триамбический икосаэдр | Медиальный триамбический икосаэдр |
| Ссылки на индексы | ДУ 47 , Вт 34 , 30/59 | ДУ 41 , Вт 34 , 30/59 |
| Элементы | Ф = 20, Е = 60 V = 32 (χ = -8) | Ф = 20, Е = 60 V = 24 (χ = -16) |
| Изоэдральные грани | 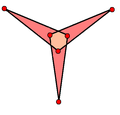 |  |
| Дуалы |  Большой дитригональный икосододекаэдр |  Дитригональный додекадодекаэдр |
| Звездчатость | ||
| Икосаэдр : W 34 | ||
 Звездчатая диаграмма | ||

В геометрии большой триамбический икосаэдр и средний триамбический икосаэдр (или среднетриамбический икосаэдр ) представляют собой визуально идентичные двойственные однородные многогранники . Внешняя поверхность также представляет De 2 f 2 звездчатку икосаэдра собой . Эти фигуры можно отличить, отметив, какие пересечения ребер являются истинными вершинами , а какие нет. На изображениях выше истинные вершины отмечены золотыми сферами, которые можно увидеть в вогнутых Y-образных областях. Альтернативно, если грани заполняются по правилу чет-нечет , внутренняя структура обеих фигур будет отличаться.
12 вершин выпуклой оболочки соответствуют вершин икосаэдра . расположению
Большой триамбический икосаэдр
[ редактировать ]Большой триамбический икосаэдр является двойником большого дитригонального икосододекаэдра U47. Он имеет 20 перевернуто-шестиугольных (треугольных) граней, по форме напоминающих трехлопастный пропеллер . Он имеет 32 вершины: 12 внешних и 20 скрытых внутри. Он имеет 60 ребер.
Лица имеют чередующиеся углы и . Сумма шести углов равна , и не как и следовало ожидать от шестиугольника, поскольку многоугольник дважды поворачивается вокруг своего центра. Двугранный угол равен .
Медиальный триамбический икосаэдр
[ редактировать ]Медиальный триамбический икосаэдр является двойником дитригонального додекадодекаэдра U41. У него 20 граней, каждая из которых представляет собой простые вогнутые изотоксальные шестиугольники или триамби. Он имеет 24 вершины: 12 внешних и 12 скрытых внутри. Он имеет 60 ребер.
Лица имеют чередующиеся углы и . Двугранный угол равен .
В отличие от большого триамбического икосаэдра, средний триамбический икосаэдр топологически представляет собой правильный многогранник индекса два. [1] Искажая триамбии в правильные шестиугольники , можно получить фактор-пространство гиперболической шестиугольной мозаики пятого порядка :
Как звездочка
[ редактировать ]Это 34-я модель Веннингера и его 9-я звездчатая икосаэдра.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Правильные многогранники (из второго индекса). Архивировано 4 марта 2016 г. в Wayback Machine , Дэвид А. Рихтер.
- Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN 0-521-09859-9 .
- Веннингер, Магнус (1983). Двойные модели . Издательство Кембриджского университета . ISBN 978-0-521-54325-5 . МР 0730208 .
- HSM Coxeter , Правильные многогранники , (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 , 3.6 6.2 Стулирование платоновых тел , стр. 96-104
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Большой триамбический икосаэдр» . Математический мир .
- Вайсштейн, Эрик В. «Срединный триамбический икосаэдр» . Математический мир .
- gratrix.net Однородные многогранники и двойники
- bulatov.org Медиальный триамбический икосаэдр Большой триамбический икосаэдр
| Известные звездочки икосаэдра | |||||||||
| Обычный | Униформа двойная | Регулярные соединения | Обычная звезда | Другие | |||||
| (Выпуклый) икосаэдр | Малый триамбический икосаэдр | Медиальный триамбический икосаэдр | Большой триамбический икосаэдр | Соединение пяти октаэдров | Соединение пяти тетраэдров | Соединение десяти тетраэдров | Большой икосаэдр | Раскопанный додекаэдр | Последняя звездочка |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией . | |||||||||









