Соединение десяти тетраэдров

Соединение десяти тетраэдров
Тип	обычное соединение
Символ Коксетера	2{5,3}[10{3,3}]2{3,5}
Индекс	УК 6 , Вт 25
Элементы (В виде соединения)	10 тетраэдров : Ф = 40, Е = 60, В = 20
Двойное соединение	Самодвойственный
Группа симметрии	икосаэдрический ( I h )
Подгруппа, ограничивающаяся одним компонентом	хиральный тетраэдр ( T )

3D модель соединения десяти тетраэдров

Соединение — одно десяти тетраэдров из пяти правильных многогранников. Этот многогранник можно рассматривать либо как звездчатую часть икосаэдра как его , либо соединение . Это соединение было впервые описано Эдмундом Гессом в 1876 году.

Его можно рассматривать как огранку правильного додекаэдра.

В качестве соединения

В виде сферической плитки

Его также можно рассматривать как соединение десяти тетраэдров с полной икосаэдрической симметрией ( I _h ). Это одно из пяти правильных соединений, построенных из идентичных платоновых тел .

Он имеет то же расположение вершин, что и додекаэдр .

Соединение пяти тетраэдров представляет собой две хиральные половины этого соединения (поэтому его можно рассматривать как «соединение двух соединений пяти тетраэдров»).

Его можно составить из соединения пяти кубов , заменив каждый куб стеллой -октангулой в вершинах куба (что приводит к «соединению пяти соединений двух тетраэдров»).

Как звездочка

Этот многогранник представляет собой звездчатую форму и икосаэдра имеет индекс модели Веннингера 25 .

Звездчатая диаграмма	звездообразования Ядро	Выпуклая оболочка
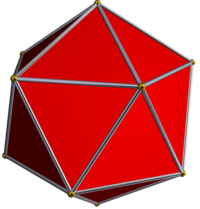	Икосаэдр	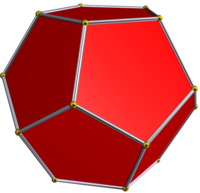Додекаэдр

В качестве огранки

Десять тетраэдров в додекаэдре.

Это также огранка додекаэдра , как показано слева. Вогнутые пентаграммы можно увидеть на соединении пятиугольных граней додекаэдра.

Как простой многогранник

Если рассматривать его как простой невыпуклый многогранник без самопересекающихся поверхностей, то он имеет 180 граней (120 треугольников и 60 вогнутых четырехугольников), 122 вершины (60 степени 3, 30 степени 4, 12 степени 5 и 20 вершин). со степенью 12) и 300 ребер, что дает эйлерову характеристику 122-300+180 = +2.

См. также

• Соединение пяти тетраэдров

Ссылки

• Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN  0-521-09859-9 .
• Коксетер, Гарольд Скотт Макдональд ; Дю Валь, П.; Флатер, ХТ; Петри, Дж. Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквиний. ISBN  978-1-899618-32-3 . МР   0676126 . (1-й Эднский университет Торонто (1938))
• HSM Coxeter , Правильные многогранники , (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8 , 3.6 Пять правильных соединений , стр. 47-50, 6.2 Стулирование платоновых тел , стр. 96-104

Внешние ссылки

• Вайсштейн, Эрик В. «10-соединение тетраэдра» . Математический мир .
• Модель VRML : [1]
• Соединения тетраэдров 5 и 10, автор Шандор Кабай, Демонстрационный проект Вольфрама .
• Клитцинг, Ричард. «3D соединение» .

Известные звездочки икосаэдра
Обычный	Униформа дуалы			Регулярные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Последняя звездочка
Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией .