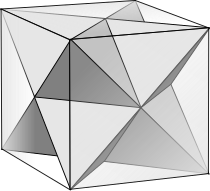
Огранка
В геометрии фасетирование или также пишется как фасетирование ) — это процесс удаления частей многоугольника , многогранника ( многогранника без создания новых вершин .
Новые ребра ограненного многогранника можно создавать по диагоналям граней или диагоналям внутреннего пространства . будет Фасетный многогранник иметь две грани на каждом ребре и создаст новые многогранники или соединения многогранников.
Огранка – это обратный или двойной процесс звездчатости . Для каждой звездчатости некоторого выпуклого многогранника существует двойственная огранка двойственного многогранника .
Фасетные многоугольники
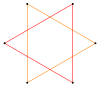
[ редактировать ]Например, правильный пятиугольник имеет одну симметричную грань, пентаграмму , а правильный шестиугольник имеет две симметричные грани: одну в виде многоугольника, а другую в виде соединения двух треугольников.
| Пентагон | Шестиугольник | Декагон | |||||||
|---|---|---|---|---|---|---|---|---|---|
 |  |  | |||||||
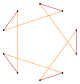
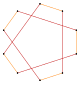
| Пентаграмма {5/2} | Звездный шестиугольник | Сложный 2{3} | Декаграмма {10/3} | Сложный 2{5} | Сложный 2{5/2} | Звездный десятиугольник | |||
 |  |  |  |  |  |  |  |  |  |
Граненые многогранники
[ редактировать ]Правильный икосаэдр можно разбить на три правильных многогранника Кеплера-Пуансо : малый звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Все они имеют 30 ребер.
| Выпуклый | Обычные звезды | ||
|---|---|---|---|
| икосаэдр | большой додекаэдр | маленький звездчатый додекаэдр | большой икосаэдр |
 |  |  |  |
Правильный додекаэдр можно разбить на один правильный многогранник Кеплера-Пуансо , три однородных звездчатых многогранника и три правильных составных многогранника . Однородные звезды и соединение пяти кубов построены по диагоналям граней . представляет Раскопанный додекаэдр собой огранку со звездчатыми гранями шестиугольника.
| Выпуклый | Регулярные соединения | ||
|---|---|---|---|
| додекаэдр | пять тетраэдров | пять кубиков | десять тетраэдров |
 |  |  |  |
История
[ редактировать ]Огранка не изучалась так широко, как звездчатость .
- В 1568 году Венцель Ямницер опубликовал свою книгу Perspectiva Corporum Regularium , в которой показано множество звездочек и граней многогранников. [1]
- В 1619 году Кеплер описал правильное соединение двух тетраэдров , помещающееся внутри куба, и которое он назвал Стеллой октангулой .
- В 1858 году Бертран вывел правильные звездчатые многогранники ( многогранники Кеплера-Пуансо ) путем огранки правильного выпуклого икосаэдра и додекаэдра .
- В 1974 году Бридж перечислил более простые грани правильных многогранников , в том числе додекаэдра .
- В 2006 году Инчбальд описал основную теорию диаграмм огранки многогранников. Для данной вершины на диаграмме показаны все возможные ребра и грани (новые грани), которые можно использовать для формирования граней исходной оболочки. Она двойственна звездчатой диаграмме двойного многогранника , которая показывает все возможные ребра и вершины некоторой грани исходной плоскости исходного ядра.
Ссылки
[ редактировать ]Примечания
[ редактировать ]- ^ Математическое сокровище: Платоновые тела Венцеля Ямнитцера Фрэнка Дж. Светца (2013): «В этом исследовании пяти Платоновых тел Ямнитцер усек, звездчатые и ограненные правильные твердые тела [...]»
Библиография
[ редактировать ]- Бертран, Ж. Заметка по теории правильных многогранников, Отчеты сессий Академии наук , 46 (1858), стр. 79–82.
- Бридж, Нью-Джерси. Огранка додекаэдра, Acta Crystallographica A30 (1974), стр. 548–552.
- Инчбальд, Г. Диаграммы фасетирования, Математический вестник , 90 (2006), стр. 253–261.
- Алан Холден « Формы, пространство и симметрия» . Нью-Йорк: Дувр, 1991. стр.94.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Огранка» . Математический мир .
- Ольшевский, Георгий. «Огранка» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.