Малый звездчатый додекаэдр

Малый звездчатый додекаэдр
Тип	Многогранник Кеплера – Пуансо
звездообразования Ядро	правильный додекаэдр
Элементы	Ф = 12, Е = 30 V = 12 (χ = -6)
Лица по сторонам	12 5
Символ Шлефли	{ 5 ⁄ 2 ,5}
Конфигурация лица	V(5 5 )/2
Символ Витхоффа	5 | 2 5 ⁄ 2
Диаграмма Кокстера
Группа симметрии	I h , H 3 , [5,3], (*532)
Ссылки	Ю 34 , С 43 , Ж 20
Характеристики	Обычный невыпуклый
( 5 ⁄ 2 ) 5 ( фигура вершины )	Большой додекаэдр ( двойной многогранник )

3D модель малого звездчатого додекаэдра

В геометрии маленький звездчатый додекаэдр представляет собой многогранник Кеплера-Пуансо , названный Артуром Кэли и имеющий символ Шлефли { 5 ⁄ 2,5 }. Это один из четырех невыпуклых правильных многогранников . Он состоит из 12 граней пентаграмм , по пять пентаграмм сходящихся в каждой вершине.

Он имеет то же расположение вершин , что и выпуклый правильный икосаэдр . Он также имеет то же расположение ребер, что и большой икосаэдр , с которым он образует вырожденную однородную составную фигуру .

Это вторая из четырех звездочек додекаэдра (включая сам исходный додекаэдр).

Маленький звездчатый додекаэдр можно построить аналогично пентаграмме, ее двумерному аналогу, путем расширения ребер (1-граней) основного многогранника до тех пор, пока не будет достигнута точка их пересечения.

Топология

Если пентаграммные грани рассматривать как 5 треугольных граней, они имеют ту же топологию поверхности, что и додекаэдр пентакиса , но с гораздо более высокими гранями равнобедренного треугольника, а высота пятиугольных пирамид отрегулирована так, что пять треугольников в пентаграмме становятся копланарными. Критический угол равен atan(2) над гранью додекаэдра.

Если мы рассматриваем его как имеющий 12 пентаграмм в качестве граней, причем эти пентаграммы встречаются в 30 ребрах и 12 вершинах, мы можем вычислить его род , используя формулу Эйлера

$V-E+F=2-2g$

и заключить, что малый звездчатый додекаэдр имеет род 4. Это наблюдение, сделанное Луи Пуансо , поначалу сбивало с толку, но Феликс Кляйн маленький звездчатый додекаэдр можно рассматривать как разветвленное покрытие римановой сферы римановой поверхностью показал в 1877 году, что род 4, с точками ветвления в центре каждой пентаграммы. Фактически эта риманова поверхность, называемая кривой Бринга , имеет наибольшее число симметрий среди всех римановых поверхностей рода 4: симметрическая группа $S_{5}$ действует как автоморфизмы

Изображения

Прозрачная модель	Модели ручной работы
(См. также: анимационный )
Сферическая черепица	Звездчатость	Сеть
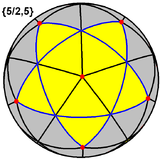Этот многогранник также представляет собой сферическую мозаику с плотностью 3. (Одна сферическая грань пентаграммы, обведенная синим цветом, закрашена желтым цветом)	Ее также можно построить как первую из трех звездочек додекаэдра ] и назвать моделью Веннингера [W20 .	× 12 Маленькие звездчатые додекаэдры можно построить из бумаги или картона, соединив вместе 12 пятигранных равнобедренных пирамид так же, как пятиугольники в правильном додекаэдре. Благодаря непрозрачному материалу он визуально представляет внешнюю часть каждой пентаграммной грани.

В искусстве

Напольная мозаика Паоло Уччелло, 1430 г.

Небольшой звездчатый додекаэдр можно увидеть в мозаике пола в базилике Святого Марка в Венеции работы Паоло Уччелло ок. 1430 . Одна и та же форма занимает центральное место в двух литографиях М.К. Эшера : «Контраст (Порядок и Хаос)» (1950) и «Гравитация» (1952).

Формулы

Для небольшого звездчатого додекаэдра с длиной ребра E:

• Окружность = ${\tfrac {E}{4}}{\Bigl (}{\sqrt {50+22{\sqrt {5}}}}{\Bigr )}$
• Площадь поверхности = $15{\Bigl (}{\sqrt {5+2{\sqrt {5}}}}{\Bigr )}E^{2}$
• Объем = ${\tfrac {5}{4}}(7+3{\sqrt {5}})E^{3}$

Связанные многогранники

Анимированная последовательность усечения из { 5 ⁄ 2 , 5} до {5, 5 ⁄ 2 }

Его выпуклая оболочка представляет собой правильный выпуклый икосаэдр . Он также разделяет свои края с большим икосаэдром ; соединение обоих представляет собой большой сложный икосододекаэдр .

Существует четыре связанных однородных многогранника, построенных как степени усечения. Дуал — это большой додекаэдр . Додекадодекаэдр — это ректификация , при которой ребра усекаются до точек.

Усеченный поскольку малый звездчатый додекаэдр можно считать вырожденным однородным многогранником, ребра и вершины совпадают, но он включен для полноты. Визуально он выглядит как правильный додекаэдр на поверхности , но у него 24 грани, попарно перекрывающиеся. Шипы обрезаются, пока не достигают плоскости пентаграммы под ними. 24 грани представляют собой 12 пятиугольников из усеченных вершин и 12 десятиугольников, имеющих форму пятиугольников с двойной обмоткой, перекрывающих первые 12 пятиугольников. Последние грани образуются путем усечения исходных пентаграмм. Когда { n ⁄ d }-угольник усекается, он становится { 2 n ⁄ d }-угольник. Например, усеченный пятиугольник { 5 ⁄ 1 } становится десятиугольником { 10 ⁄ 1 }, поэтому усечение пентаграммы { 5 ⁄ 2 } становится пятиугольником с двойной обмоткой { 10 ⁄ 2 } (общий множитель между 10 и 2 означает, что мы посещаем каждую вершину дважды, чтобы завершить многоугольник).

Звездочки додекаэдра
Платоново твердое тело	Твердые тела Кеплера – Пуансо
Додекаэдр	Малый звездчатый додекаэдр	Большой додекаэдр	Большой звездчатый додекаэдр

Имя	Малый звездчатый додекаэдр	Усеченный малый звездчатый додекаэдр	Додекадодекаэдр	Усечено большой додекаэдр	Большой додекаэдр
Коксетер-Дынкин диаграмма
Картина

См. также

• Соединение малого звездчатого додекаэдра и большого додекаэдра.

Дальнейшее чтение

• Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета . ISBN  0-521-09859-9 .
• Вебер, Маттиас (2005), «Маленький звездчатый додекаэдр Кеплера как риманова поверхность» , Pacific J. Math. , 220 : 167–182, doi : 10.2140/pjm.2005.220.167

Внешние ссылки

• Вайсштейн, Эрик В. , « Маленький звездчатый додекаэдр » (« Равномерный многогранник ») в MathWorld .