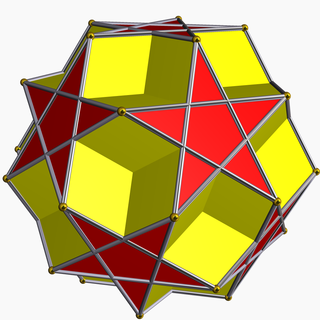
Додекадодекаэдр
| Додекадодекаэдр | |
|---|---|
 | |
| Тип | Однородный звездчатый многогранник |
| Элементы | Ф = 24, Е = 60 V = 30 (χ = −6) |
| Лица по сторонам | 12{5}+12{5/2} |
| Диаграмма Кокстера | |
| Символ Витхоффа | 2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4 |
| Группа симметрии | I h , [5,3], *532 |
| Ссылки на индексы | Ю 36 , С 45 , Ж 73 |
| Двойной многогранник | Медиальный ромбический триаконтаэдр |
| Вершинная фигура |  5.5/2.5.5/2 |
| Аббревиатура Бауэрса | Делал |

В геометрии додекадодекаэдр , — невыпуклый однородный многогранник имеющий индекс U36 . [1] Это выпрямление большого додекаэдра (и его двойника, малого звездчатого додекаэдра ). Он был открыт независимо Гессом ( 1878 г. ), Бадуро ( 1881 г. ) и Питчем ( 1882 г. ).
Края этой модели образуют 10 центральных шестиугольников , которые, проецируясь на сферу , становятся 10 большими кругами . Эти 10, вместе с большими кругами из проекций двух других многогранников, образуют 31 большой круг сферического икосаэдра, используемый при строительстве геодезических куполов .
Конструкции Витхоффа
[ редактировать ]Он имеет четыре конструкции Витгофа между четырьмя семействами треугольников Шварца : 2 | 5 5/2 , 2 | 5 5/3 , 2 | 5/2 5/4 , 2 | 5/3 5/4 , но представляют идентичные результаты. Аналогичным образом можно задать четыре расширенных символа Шлефли : r{5/2,5}, r{5/3,5}, r{5/2,5/4} и r{5/3,5/4}. или в виде диаграмм Кокстера-Динкина : ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , и
, и ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Сеть
[ редактировать ]Форму с таким же внешним видом, как у додекадодекаэдра, можно построить, сложив эти сетки:
12 пентаграмм и 20 ромбических Необходимо гроздей. Однако эта конструкция заменяет пересекающиеся пятиугольные грани додекадодекаэдра непересекающимися наборами ромбов, поэтому она не создает ту же внутреннюю структуру.
Связанные многогранники
[ редактировать ]Его выпуклая оболочка — икосододекаэдр . Он также имеет общее расположение ребер с малым додекагемикосаэдром (имеющим общие пентаграммные грани) и с большим додекагемикосаэдром (имеющим общие пятиугольные грани).
 Додекадодекаэдр |  Малый додекагемикосаэдр |
 Большой додекагемикосаэдр |  Икосододекаэдр ( выпуклая оболочка ) |

Этот многогранник можно считать выпрямленным большим додекаэдром . Это центр последовательности усечения между малым звездчатым додекаэдром и большим додекаэдром :
Усеченный . похож на додекаэдр малый звездчатый додекаэдр внешне , но у него 24 грани: 12 пятиугольников из усеченных вершин и 12 перекрывающихся в виде (усеченных пентаграмм) Усечение додекадодекаэдра само по себе неоднородно, и попытка сделать его однородным приводит к вырожденному многограннику (который выглядит как небольшой ромбидодекаэдр с {10/2} многоугольниками, заполняющими додекаэдрический набор отверстий), но он имеет равномерное квазиусечение, усеченный додекадодекаэдр .
| Имя | Малый звездчатый додекаэдр | Усеченный малый звездчатый додекаэдр | Додекадодекаэдр | Усечено большой додекаэдр | Большой додекаэдр |
|---|---|---|---|---|---|
| Коксетер-Дынкин диаграмма | |||||
| Картина |  |  |  |  |  |
Это топологически эквивалентно фактор-пространству гиперболической , пятиугольной мозаики четвертого порядка искажая пентаграммы обратно в правильные пятиугольники . Таким образом, топологически это правильный многогранник индекса два: [2] [3]
Графики додекадодекаэдра (слева) и двойственного ему (справа), построенного на кривой Бринга . | |
 | 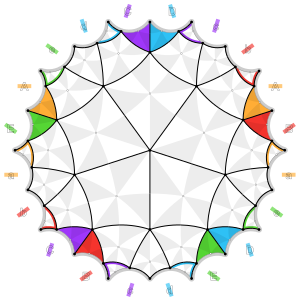 |
| 24 пятиугольника 11 целых, 10 разрезанных пополам, 2 разрезаны на пять частей, 1 разрезан на десять частей. | 30 квадратов 20 целых, 10 разрезанных пополам. |
Медиальный ромбический триаконтаэдр
[ редактировать ]| Медиальный ромбический триаконтаэдр | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо |  |
| Элементы | Ф = 30, Е = 60 V = 24 (χ = −6) |
| Группа симметрии | I h , [5,3], *532 |
| Ссылки на индексы | ДУ 36 |
| двойной многогранник | Додекадодекаэдр |
Медиальный ромбический триаконтаэдр является двойником додекадодекаэдра. Он имеет 30 пересекающихся ромбических граней.
Связанная гиперболическая мозаика
[ редактировать ]Это топологически эквивалентно фактор-пространству гиперболической квадратной мозаики пятого порядка , искажающей ромбы в квадраты . Таким образом, топологически это правильный многогранник индекса два: [4]
Обратите внимание, что квадратная мозаика 5-го порядка двойственна пятиугольной мозаике 4-го порядка , а фактор-пространство пятиугольной мозаики 4-го порядка топологически эквивалентно двойственному медиальному ромбическому триаконтаэдру, додекадодекаэдру.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Медер, Роман. «36: додекадодекаэдр» . www.mathconsult.ch . Проверено 3 февраля 2020 г.
- ^ Правильные многогранники (из второго индекса). Архивировано 4 марта 2016 г. в Wayback Machine , Дэвид А. Рихтер.
- ^ Код Голея на додекадодекаэдре. Архивировано 18 октября 2018 г. в Wayback Machine , Дэвид А. Рихтер.
- ^ Правильные многогранники (из второго индекса). Архивировано 4 марта 2016 г. в Wayback Machine , Дэвид А. Рихтер.
- Бадуро (1881), «Мемуары о равнобедренных фигурах», Journal de l'École Polytechnique , 49 : 47–172.
- Гесс, Эдмунд (1878), Четыре архимедовых многогранника высшего рода , Кассель. Кей, ЖФМ 10.0346.03
- Питч (1882), «О полуправильных звездчатых многогранниках», Журнал для средней школы , 7 , JFM 14.0448.01
- Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , МР 0730208
