Октагемиоктаэдр

Октагемиоктаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф = 12, Е = 24 V = 12 (χ = 0)
Лица по сторонам	8{3}+4{6}
Диаграмма Кокстера
Символ Витхоффа	3/2 3 | 3
Группа симметрии	О ч , [4,3], *432
Ссылки на индексы	У 03 , С 37 , Вт 68
Двойной многогранник	Октагемиоктакрон
Вершинная фигура	3.6.3/2.6
Аббревиатура Бауэрса	Проснуться

3D модель октагемиоктаэдра

В геометрии октагемиоктаэдр представляет или аллелотетратетраэдр собой многогранник , обозначаемый индексом U3 _. невыпуклый однородный У него 12 граней (8 треугольников и 4 шестиугольника ), 24 ребра и 12 вершин . Его вершинная фигура представляет собой перекрещенный четырехугольник .

Это один из девяти полумногогранников , у которого 4 шестиугольные через центр модели проходят грани.

Ориентируемость

Это единственный ориентируемый полуполиэдр и единственный однородный многогранник с эйлеровой характеристикой нулевой (топологический тор ).

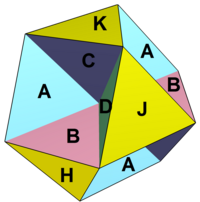Октагемиоктаэдр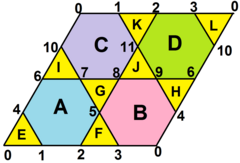

Топологическую сеть граней можно представить в виде ромба, разделенного на 8 треугольников и 4 шестиугольника. Все дефекты угла вершины равны нулю.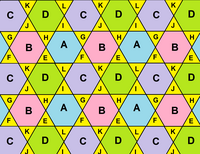

Сеть представляет собой область тригексагональной плоскости замощения .

Связанные многогранники

Он разделяет расположение вершин и расположение ребер с кубооктаэдром (имеющим общие треугольные грани) и с кубогемиоктаэдром (имеющим общие шестиугольные грани).

По конструкции Витгофа он имеет тетраэдрическую симметрию (T _d ), как и конструкция ромбитетратраэдра для кубооктаэдра , с чередующимися треугольниками с перевернутой ориентацией. Без чередующихся треугольников имеет октаэдрическую симметрию (О _h ). В этом отношении она подобна поверхности Морена , которая имеет четырехкратную симметрию, если не учитывать ориентацию, и двукратную симметрию в противном случае. Однако октагемиоктаэдр имеет более высокую степень симметрии и имеет род 1, а не 0.

Кубооктаэдр		Кубогемиоктаэдр	Октагемиоктаэдр
Октаэдрическая симметрия	Тетраэдрическая симметрия		Октаэдрическая симметрия	Тетраэдрическая симметрия
2 | 3 4	3 3 | 2	4/3 4 | 3 (двойная обложка)		3/2 3 | 3

---

Октагемиоктакрон

Октагемиоктакрон
Тип	Звездный многогранник
Лицо	—
Элементы	Ф = 12, Е = 24 V = 12 (χ = 0)
Группа симметрии	О ч , [4,3], *432
Ссылки на индексы	ДВА 03
двойной многогранник	Октагемиоктаэдр

Октагемиоктаэдр — двойник октагемиоктаэдра и один из девяти двойственных полумногогранников . Визуально он неотличим от гексагемиоктакрона .

Поскольку у полумногогранников грани проходят через центр, у двойственных фигур соответствующие вершины находятся в бесконечности; собственно, на реальной проективной плоскости на бесконечности. В » Магнуса Веннингера они «Двойных моделях представлены в виде пересекающихся призм , каждая из которых простирается в обоих направлениях до одной и той же вершины на бесконечности, чтобы сохранить симметрию. На практике призмы модели обрезаются в определенном месте, удобном для производителя. Веннингер предположил, что эти фигуры являются членами нового класса звездчатых фигур, называемых звездчатыми до бесконечности . Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.

Октагемиоктакрон имеет четыре вершины, удаленные на бесконечность.

См. также

• Соединение пяти октагемиоктаэдров.
• Полукуб . Четыре вершины на бесконечности соответствуют четырем вершинам этого абстрактного многогранника.

Ссылки

• Веннингер, Магнус (2003) [1983], Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN  978-0-521-54325-5 , MR   0730208 (Страница 101, Двойники (девяти) полумногогранников)

Внешние ссылки

• Вайсштейн, Эрик В. , « Октахемиоктаэдр » (« Однородный многогранник ») в MathWorld .
• Вайсштейн, Эрик В. «Октагемиоктакрон» . Математический мир .
• Однородные многогранники и двойники