Большой курносый икосододекаэдр

Большой курносый икосододекаэдр
Тип	Однородный звездчатый многогранник
Элементы	Ф = 92, Е = 150 V = 60 (χ = 2)
Лица по сторонам	(20+60){3}+12{5/2}
Диаграмма Кокстера
Символ Витхоффа	| 2 5/2 3
Группа симметрии	Я, [5,3] + , 532
Ссылки на индексы	Ю 57 , С 88 , Ж 113
Двойной многогранник	Большой пятиугольный шестиконтаэдр
Вершинная фигура	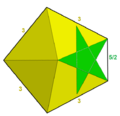3 4 .5/2
Аббревиатура Бауэрса	Госид

3D-модель большого курносого икосододекаэдра

В геометрии большой курносый икосододекаэдр представляет собой невыпуклый однородный многогранник , имеющий индекс _U57 . У него 92 грани (80 треугольников и 12 пентаграмм ), 150 ребер и 60 вершин. Его можно представить символом Шлефли sr{ 5 ⁄ 2,3 } и диаграмма Кокстера-Дынкина .

Этот многогранник является курносым членом семейства, в которое входят большой икосаэдр , большой звездчатый додекаэдр и большой икосододекаэдр .

В книге Модели многогранников « Магнуса Веннингера » многогранник ошибочно назван большим перевернутым курносым икосододекаэдром , и наоборот.

Декартовы координаты

Позволять $\xi \approx 0.3990206456527105$ быть положительным нулем многочлена $x^{3}+2x^{2}-\phi ^{-2}$, где $\phi$ это золотое сечение . Пусть точка $p$ быть предоставлено

$p={\begin{pmatrix}\xi \\\phi ^{-2}-\phi ^{-2}\xi \\-\phi ^{-3}+\phi ^{-1}\xi +2\phi ^{-1}\xi ^{2}\end{pmatrix}}$.

Пусть матрица $M$ быть предоставлено

$M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}$.

$M$ это вращение вокруг оси $(1,0,\phi )$ под углом $2\pi /5$, против часовой стрелки. Пусть линейные преобразования $T_{0},\ldots ,T_{11}$ быть преобразованиями, которые посылают точку $(x,y,z)$ к четным перестановкам $(\pm x,\pm y,\pm z)$ с четным количеством знаков минус. Преобразования $T_{i}$ составляют группу вращательных симметрий правильного тетраэдра .Преобразования $T_{i}M^{j}$ $(i=0,\ldots ,11$, $j=0,\ldots ,4)$ составляют группу вращательных симметрий правильного икосаэдра .Тогда 60 баллов $T_{i}M^{j}p$ являются вершинами большого курносого икосаэдра. Длина ребра равна $2\xi {\sqrt {1-\xi }}$, радиус описанной окружности равен $\xi {\sqrt {2-\xi }}$, а средний радиус равен $\xi$.

Для большого курносого икосододекаэдра, длина ребра которого равна 1,радиус описанной окружности

$R={\frac {1}{2}}{\sqrt {\frac {2-\xi }{1-\xi }}}\approx 0.8160806747999234$

Его средний радиус

$r={\frac {1}{2}}{\sqrt {\frac {1}{1-\xi }}}\approx 0.6449710596467862$

Четыре положительных вещественных корня секстика в R ² , $$4096R^{12}-27648R^{10}+47104R^{8}-35776R^{6}+13872R^{4}-2696R^{2}+209=0$$Это, по порядку, радиусы описанной окружности большого ретроносодекаэдра (U ₇₄ ), большого курносого икосододекаэдра (U ₅₇ ), большого перевернутого курносого икосододекаэдра (U ₆₉ ) и курносого додекаэдра (U ₂₉ ).

Связанные многогранники

Большой пятиугольный шестиконтаэдр

Большой пятиугольный шестиконтаэдр
Тип	Звездный многогранник
Лицо
Элементы	Ф = 60, Е = 150 V = 92 (х = 2)
Группа симметрии	Я, [5,3] + , 532
Ссылки на индексы	ТЫ 57
двойной многогранник	Большой курносый икосододекаэдр

3D-модель большого пятиугольного шестиконтаэдра

Большой пятиугольный шестигранник (или большой лепестковидный дитриаконтаэдр ) представляет собой невыпуклый изоэдрический многогранник и двойственный однородному большому курносому икосододекаэдру . Он имеет 60 пересекающихся неправильных пятиугольных граней, 120 ребер и 92 вершины.

Пропорции

Обозначим золотое сечение через $\phi$. Позволять $\xi \approx -0.199\,510\,322\,83$ быть отрицательным нулем многочлена $P=8x^{3}-8x^{2}+\phi ^{-2}$. Тогда каждая пятиугольная грань имеет четыре равных угла $\arccos(\xi )\approx 101.508\,325\,512\,64^{\circ }$ и один угол $\arccos(-\phi ^{-1}+\phi ^{-2}\xi )\approx 133.966\,697\,949\,42^{\circ }$. Каждая грань имеет три длинных и два коротких края. Соотношение $l$ между длинами длинного и короткого ребер определяется выражением

$l={\frac {2-4\xi ^{2}}{1-2\xi }}\approx 1.315\,765\,089\,00$.

Двугранный угол равен $\arccos(\xi /(\xi +1))\approx 104.432\,268\,611\,86^{\circ }$. Часть каждой грани лежит внутри твердого тела и поэтому невидима в твердотельных моделях. Два других нуля многочлена $P$ играют аналогичную роль в описании большого перевернутого пятиугольного гексеконтаэдра и большого пентаграммного гексеконтаэдра .

См. также

• Список однородных многогранников
• Большой перевернутый курносый икосододекаэдр.
• Большой ретроносый икосододекаэдр

Ссылки

• Веннингер, Магнус (1983), Двойные модели , Издательство Кембриджского университета , ISBN  978-0-521-54325-5 , МР   0730208

Внешние ссылки

• Вайсштейн, Эрик В. «Большой пятиугольный шестиконтаэдр» . Математический мир .
• Вайсштейн, Эрик В. «Большой курносый икосододекаэдр» . Математический мир .