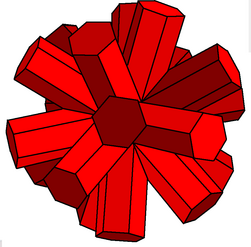
Малый додекегемикосакрон
| Малый додекегемикосакрон | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо | — |
| Элементы | Ф = 30, Е = 60 V = 22 (χ = −8) |
| Группа симметрии | I h , [5,3], *532 |
| Ссылки на индексы | ДУ 62 |
| двойной многогранник | Малый додекагемикосаэдр |
В геометрии малый додекагемикосакрон является двойником малого додекагемикосаэдра и является одним из девяти двойственных полуполиэдров . Визуально он неотличим от большого додекегемикозакрона .
Поскольку у полумногогранников грани проходят через центр, у двойственных фигур соответствующие вершины находятся в бесконечности; собственно, на реальной проективной плоскости на бесконечности. [1] В » Магнуса Веннингера они «Двойных моделях представлены в виде пересекающихся призм , каждая из которых простирается в обоих направлениях до одной и той же вершины на бесконечности, чтобы сохранить симметрию. На практике призмы модели обрезаются в определенном месте, удобном для производителя. Веннингер предположил, что эти фигуры являются членами нового класса звездчатых фигур, называемых звездчатыми до бесконечности . Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.
Поскольку маленький додекагемикосаэдр имеет десять шестиугольных граней, проходящих через центр модели, его можно рассматривать как имеющий десять вершин, обращенных в бесконечность.
См. также
[ редактировать ]- Полуикосаэдр . Десять вершин на бесконечности соответствуют 10 вершинам этого абстрактного многогранника.
Ссылки
[ редактировать ]- ^ ( Веннингер 2003 , стр. 101 )
- Веннингер, Магнус (2003) [1983], Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Страница 101, Двойники (девяти) полумногогранников)
Внешние ссылки
[ редактировать ] | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |