Символ Витхоффа


В геометрии символ Витгофа представляет собой обозначение, представляющее конструкцию Витгофа однородного многогранника или плоской мозаики внутри треугольника Шварца . Впервые его использовали Коксетер , Лонге-Хиггинс и Миллер при перечислении однородных многогранников. Позже диаграмма Кокстера была разработана для обозначения однородных многогранников и сот в n-мерном пространстве внутри фундаментального симплекса.
Символ Витхоффа состоит из трех цифр и вертикальной черты. Он представляет собой один однородный многогранник или мозаику, хотя одна и та же мозаика/многогранник может иметь разные символы Витхоффа от разных генераторов симметрии. Например, обычный куб можно представить как 3 | 4 с Oh симметрией 2 и 2 4 | 2 в виде квадратной призмы с двумя цветами и D 4h симметрией , а также 2 2 2 | с 3 цветами и D 2h симметрией .
С небольшим расширением символ Витхоффа можно применить ко всем однородным многогранникам. Однако методы построения не приводят ко всем однородным мозаикам в евклидовом или гиперболическом пространстве.
Описание [ править ]
Конструкция Витгофа начинается с выбора образующей точки фундаментального треугольника. Эту точку нужно выбрать на равном расстоянии от всех ребер, на которые она не лежит, и затем от нее к каждому такому ребру опустить перпендикуляр.
Три числа в символе Витгофа, p , q и r , обозначают углы треугольника Шварца, использованного в конструкции, которые являются π / п , π / q и π / r радиан соответственно. Треугольник также обозначается теми же числами, записанными ( p q r ). Вертикальная черта в символе указывает категориальное положение образующей точки внутри фундаментального треугольника согласно следующему:
- р | q r указывает, что образующая лежит в углу p ,
- п q | r указывает, что генератор находится на границе между p и q ,
- п q р | указывает на то, что образующая находится внутри треугольника.
В этих обозначениях зеркала помечены порядком отражения противоположной вершины. Значения p , q , r отображаются перед полосой, если соответствующее зеркало активно.
Специальное использование имеет символ | p q r , который предназначен для случая, когда все зеркала активны, но отраженные изображения с нечетными номерами игнорируются. Полученная фигура имеет только вращательную симметрию.
Точка генератора может быть включена или выключена для каждого зеркала, активирована или нет. Это различие создает 8 (2 3 ) возможные формы, но невозможна та, где точка генератора находится на всех зеркалах. Символ, который обычно относится к этому, повторно используется для курносых мозаик.
Символ Витхоффа функционально похож на более общую диаграмму Кокстера-Динкина , в которой каждый узел представляет собой зеркало, а дуги между ними, отмеченные цифрами, — углы между зеркалами. (Дуга, представляющая прямой угол, опущена.) Узел обведен кружком, если образующая точка не находится на зеркале.
Пример сферических, евклидовых и гиперболических мозаик на прямоугольных треугольниках [ править ]
Основные треугольники нарисованы чередующимися цветами в зеркальном отображении. Последовательность треугольников ( p 3 2) меняется от сферической ( p = 3, 4, 5) к евклидовой ( p = 6) и гиперболической ( p ≥ 7). Гиперболические мозаики показаны в виде проекции диска Пуанкаре .
| Символ Витхоффа | д | п 2 | 2 кв | п | 2 | п q | 2 р | д | р | q 2 | п q | 2 | п q 2 | | | п q 2 |
|---|---|---|---|---|---|---|---|---|
| Диаграмма Кокстера | ||||||||
| Вершинная фигура | п д | д .2 п .2 п | п . q . п . д | п .2 q .2 q | д п | п .4. д .4 | 4,2 п .2 q | 3.3. п .3. д |
| Фонд. треугольники | 7 форм и курносый | |||||||
(3 3 2)  | 3 | 3 2  3 3 | 2 3 | 3  3.6.6 | 2 | 3 3  3.3.3.3 | 2 3 | 3  3.6.6 | 3 | 3 2  3 3 | 3 3 | 2  3.4.3.4 | 3 3 2 |  4.6.6 | | 3 3 2  3.3.3.3.3 |
(4 3 2)  | 3 | 4 2  4 3 | 2 3 | 4  3.8.8 | 2 | 4 3  3.4.3.4 | 2 4 | 3  4.6.6 | 4 | 3 2  3 4 | 4 3 | 2  3.4.4.4 | 4 3 2 |  4.6.8 | | 4 3 2  3.3.3.3.4 |
(5 3 2)  | 3 | 5 2  5 3 | 2 3 | 5  3.10.10 | 2 | 5 3  3.5.3.5 | 2 5 | 3  5.6.6 | 5 | 3 2  3 5 | 5 3 | 2  3.4.5.4 | 5 3 2 |  4.6.10 | | 5 3 2  3.3.3.3.5 |
(6 3 2)  | 3 | 6 2  6 3 | 2 3 | 6  3.12.12 | 2 | 6 3  3.6.3.6 | 2 6 | 3  6.6.6 | 6 | 3 2  3 6 | 6 3 | 2  3.4.6.4 | 6 3 2 |  4.6.12 | | 6 3 2  3.3.3.3.6 |
(7 3 2)  | 3 | 7 2  7 3 | 2 3 | 7  3.14.14 | 2 | 7 3  3.7.3.7 | 2 7 | 3  7.6.6 | 7 | 3 2  3 7 | 7 3 | 2  3.4.7.4 | 7 3 2 |  4.6.14 | | 7 3 2  3.3.3.3.7 |
(8 3 2)  | 3 | 8 2  8 3 | 2 3 | 8  3.16.16 | 2 | 8 3  3.8.3.8 | 2 8 | 3  8.6.6 | 8 | 3 2  3 8 | 8 3 | 2  3.4.8.4 | 8 3 2 |  4.6.16 | | 8 3 2  3.3.3.3.8 |
(∞ 3 2)  | 3 | ∞ 2  ∞ 3 | 2 3 | ∞  3.∞.∞ | 2 | ∞ 3  3.∞.3.∞ | 2 ∞ | 3  ∞.6.6 | ∞ | 3 2 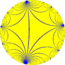 3 ∞ | ∞ 3 | 2  3.4.∞.4 | ∞ 3 2 |  4.6.∞ | | ∞ 3 2  3.3.3.3.∞ |
См. также [ править ]
- Правильный многогранник
- Правильный многогранник
- Список однородных мозаик
- Равномерные мозаики в гиперболической плоскости
- Список однородных многогранников
- Список однородных многогранников по треугольнику Шварца
- Списки однородных мозаик на сфере, плоскости и гиперболической плоскости.
Ссылки [ править ]
- Кокстера Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (Глава V: Калейдоскоп, раздел: 5.7 Конструкция Витхоффа)
- Коксетер Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 3: Конструкция Витгофа для однородных многогранников)
- Коксетер , Лонге-Хиггинс, Миллер, Равномерные многогранники , Фил. Пер. 1954, 246 А, 401–50.
- Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN 0-521-09859-9 . стр. 9–10.
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Символ Витхоффа» . Математический мир .
- Символ Витхоффа
- Апплет Грега Игана для отображения однородных многогранников с использованием метода построения Витхоффа.
- Рендеринг метода строительства Витхоффа в Shadertoy.
- KaleidoTile 3 Бесплатное образовательное программное обеспечение для Windows от Джеффри Уикса , с помощью которого было создано множество изображений на странице.
- Хэтч, Дон. «Гиперболические плоские мозаики» .