Список однородных многогранников по треугольнику Шварца

существует множество связей Между однородными многогранниками . Конструкция Витгофа позволяет построить почти все однородные многогранники из остроугольных и тупоугольных треугольников Шварца . Числа, которые можно использовать для обозначения сторон недвугранного острого или тупоугольного треугольника Шварца, который не обязательно приводит только к вырожденным однородным многогранникам, - это 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 и 5/4 (но числа с числителем 4 и числа с числителем 5 не могут встречаться вместе). (Можно также использовать 4/2, но это приводит только к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общий делитель.) Существует 44 таких треугольника Шварца (5 с тетраэдрической симметрией , 7 с октаэдрической симметрией и 32 с икосаэдрической симметрией ), которые , вместе с бесконечным семейством двугранных треугольников Шварца может образовывать почти все невырожденные однородные многогранники. Многие вырожденные однородные многогранники с полностью совпадающими вершинами, ребрами или гранями также могут быть созданы с помощью конструкции Витхоффа, а те, которые возникают из треугольников Шварца, не использующих 4/2, также приведены в таблицах ниже вместе со своими невырожденными аналогами. . Треугольники рефлекса Шварца не включены, поскольку они просто создают дубликаты или вырождения; однако некоторые из них упомянуты вне таблиц, поскольку они применимы к трем из курносые многогранники .
Существует несколько не витоффовых однородных многогранников, которые не могут породить никакие треугольники Шварца; однако большинство из них можно сгенерировать с помощью конструкции Витгофа в виде двойных накрытий (невитоффов многогранник покрывается дважды, а не один раз) или с помощью нескольких дополнительных совпадающих граней, которые необходимо отбросить, чтобы на каждом ребре оставалось не более двух граней (см. Всеусеченный многогранник#Другие четносторонние невыпуклые многогранники ). Такие многогранники отмечены в этом списке звездочкой. Единственные однородные многогранники, которые до сих пор не могут быть порождены конструкцией Витхоффа, - это большой диромбикосидодекаэдр и большой диснубированный диромбидодекаэдр .
Каждая мозаика из треугольников Шварца на сфере может покрывать сферу только один раз или вместо этого может оборачиваться вокруг сферы целое число раз, пересекаясь при этом. Число оборотов мозаики вокруг сферы представляет собой плотность мозаики и обозначается μ.
Короткие названия многогранников Джонатана Бауэрса, известные как аббревиатуры Бауэрса, используются вместо полных названий многогранников для экономии места. [1] Также указан индекс Медера. За исключением двугранных треугольников Шварца, треугольники Шварца упорядочены по плотности.
Перечислены также аналогичные случаи евклидовых разбиений и кратко и не полностью обсуждены случаи гиперболических разбиений.
Мёбиус и чёрные треугольники
[ редактировать ]Имеется 4 сферических треугольника с углами π/p, π/q, π/r, где (pqr) — целые числа: ( Коксетер , «Равномерные многогранники», 1954)
- (2 2 р) — Двугранник
- (2 3 3) – Тетраэдрический
- (2 3 4) – Октаэдрический
- (2 3 5) – Икосаэдр
Их называют треугольниками Мёбиуса.
Кроме того, треугольники Шварца учитывают (pqr), которые являются рациональными числами. Каждый из них можно отнести к одному из четырех вышеперечисленных наборов.
| Плотность (мк) | двугранный | Тетраэдрический | Октаэдрический | икосаэдрический |
|---|---|---|---|---|
| д | (2 2 н / д ) | |||
| 1 | (2 3 3) | (2 3 4) | (2 3 5) | |
| 2 | (3/2 3 3) | (3/2 4 4) | (3/2 5 5), (5/2 3 3) | |
| 3 | (2 3/2 3) | (2 5/2 5) | ||
| 4 | (3 4/3 4) | (3 5/3 5) | ||
| 5 | (2 3/2 3/2) | (2 3/2 4) | ||
| 6 | (3/2 3/2 3/2) | (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) | ||
| 7 | (2 3 4/3) | (2 3 5/2) | ||
| 8 | (3/2 5/2 5) | |||
| 9 | (2 5/3 5) | |||
| 10 | (3 5/3 5/2), (3 5/4 5) | |||
| 11 | (2 3/2 4/3) | (2 3/2 5) | ||
| 13 | (2 3 5/3) | |||
| 14 | (3/2 4/3 4/3) | (3/2 5/2 5/2), (3 3 5/4) | ||
| 16 | (3 5/4 5/2) | |||
| 17 | (2 3/2 5/2) | |||
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) | |||
| 19 | (2 3 5/4) | |||
| 21 | (2 5/4 5/2) | |||
| 22 | (3/2 3/2 5/2) | |||
| 23 | (2 3/2 5/3) | |||
| 26 | (3/2 5/3 5/3) | |||
| 27 | (2 5/4 5/3) | |||
| 29 | (2 3/2 5/4) | |||
| 32 | (3/2 5/4 5/3) | |||
| 34 | (3/2 3/2 5/4) | |||
| 38 | (3/2 5/4 5/4) | |||
| 42 | (5/4 5/4 5/4) |
Хотя многогранник обычно имеет ту же плотность, что и треугольник Шварца, из которого он создан, это не всегда так. Во-первых, многогранники, грани которых проходят через центр модели (в том числе полумногогранники , большой диромбикосододекаэдр и большой диспубированный диромбидодекаэдр ), не имеют четко определенной плотности. Во-вторых, искажение, необходимое для восстановления однородности при замене сферического многогранника на его плоский аналог, может привести к тому, что грани пройдут через центр многогранника и отойдут от другой стороны, изменяя плотность. Это происходит в следующих случаях:
- Большой усеченный кубооктаэдр , 2 3 4/3 |. Хотя треугольник Шварца (2 3 4/3) имеет плотность 7, восстановление однородности проталкивает восемь шестиугольников через центр, давая плотность |7 − 8| = 1, то же самое, что и у колунарного треугольника Шварца (2 3 4), который имеет те же большие круги.
- Усеченный додекадодекаэдр , 2 5/3 5 |. Хотя треугольник Шварца (2 5/3 5) имеет плотность 9, восстановление однородности проталкивает двенадцать декагонов через центр, давая плотность |9 − 12| = 3, то же самое, что и у столбчатого треугольника Шварца (2 5/2 5), который имеет те же большие круги.
- Три курносых многогранника: большой икосаэдр | 2 3/2 3/2, небольшой ретроносый икосикосододекаэдр | 3/2 3/2 5/2 и великий ретроносый икосододекаэдр | 2 3/2 5/3. Здесь фигуры вершин были искажены в пентаграммы или гексаграммы, а не в пятиугольники или шестиугольники, в результате чего все курносые треугольники прошли через центр и получили плотности |5 − 12| = 7, |22 − 60| = 38 и |23 − 60| = 37 соответственно. Эти плотности такие же, как у колунарно - рефлекторных треугольников Шварца, которые не включены выше. Таким образом, можно считать, что большой икосаэдр произошел из (2/3 3 3) или (2 3 3/4), малый ретроносый икосикосододекаэдр - из (3 3 5/8) или (3 3/4 5/3), и большой ретроносый икосододекаэдр из (2/3 3 5/2), (2 3/4 5/3) или (2 3 5/7). (Коксетер, «Равномерные многогранники», 1954 г.)
Сводная таблица
[ редактировать ]

Существует семь точек-генераторов с каждым набором p,q,r (и несколько специальных форм):
| Общий | Прямоугольный треугольник (r=2) | ||||||
|---|---|---|---|---|---|---|---|
| Описание | Витхофф символ | Вертекс конфигурация | Коксетер диаграмма | Витхофф символ | Вертекс конфигурация | Шлефли символ | Коксетер диаграмма |
| регулярный и квазирегулярный | д | пиар | (пр) д | д | п 2 | п д | {п, д} | ||
| р | qr | (qr) п | р | q 2 | д п | {д, р} | |||
| р | ПК | (кп) р | 2 | ПК | (кп) 2 | т 1 {p,q} | |||
| усечено и расширенный | qр | п | q.2p.r.2p | д 2 | п | q.2p.2p | т 0,1 {p,q} | ||
| пр | д | п.2q.r.2q | р 2 | д | п. 2кв.2кв | т 0,1 {q,p} | |||
| ПК | р | 2р.к.2р.п | ПК | 2 | 4.q.4.p | т 0,2 {p,q} | |||
| беспристрастный | пкр | | 2р.2д.2п | кв 2 | | 4.2к.2п | т 0,1,2 {p,q} | ||
| ПК р s | | 2п.2кв.-2п.-2кв. | - | п 2 р s | | 2п.4.-2п. 4 / 3 | - | ||
| пренебрегать | | пкр | 3.r.3.q.3.p | | ПК 2 | 3.3.q.3.p | ср{п,q} | ||
| | pqrs | (4.п.4.к.4.р.4.с)/2 | - | - | - | - | ||
Есть четыре особых случая:
- ПК р
s | – Это смесь pqr | и ПК | . Оба символа pqr | и ПК | создать общий базовый многогранник с некоторыми дополнительными гранями. Обозначение pq р
s | затем представляет базовый многогранник, состоящий из граней, общих для обоих pqr | и ПК | . - | pqr — формам Snub (чередующимся) присваивается этот неиспользуемый в противном случае символ.
- | pqrs - уникальная курносая форма для U75 , которую невозможно построить по Витхоффу с использованием треугольных фундаментальных областей. В этот символ Витгофа включены четыре числа, поскольку этот многогранник имеет тетрагональную сферическую фундаментальную область.
- | (p) q (r) s - уникальная курносая форма фигуры Скиллинга , которая не является конструируемой по Витхоффу.
Эта таблица преобразования символа Витхоффа в конфигурацию вершин не работает для исключительных пяти перечисленных выше многогранников, плотности которых не соответствуют плотностям образующих их мозаик треугольника Шварца. В этих случаях фигура вершины сильно искажается для достижения единообразия с плоскими гранями: в первых двух случаях это тупоугольный треугольник вместо остроугольного треугольника, а в последних трех - пентаграмма или гексаграмма вместо пятиугольника или шестиугольника. дважды обмотав центр. Это приводит к тому, что некоторые грани проталкиваются сквозь многогранник по сравнению с топологически эквивалентными формами без искажения фигуры вершины и выходят ретроградно с другой стороны. [2]
В таблицах ниже красным фоном отмечены вырожденные многогранники. Зелёным фоном отмечены выпуклые однородные многогранники.
Двухгранный (призматический)
[ редактировать ]В двугранных треугольниках Шварца два числа равны 2, а третье может быть любым рациональным числом, строго большим 1.
- (2 2 n / d ) – вырождено, если НОД( n , d ) > 1.
Многие многогранники с двугранной симметрией имеют двуугольные грани, что делает их вырожденными многогранниками (например, диэдры и осоэдры ). Столбцы таблицы, дающие только вырожденные однородные многогранники, не включены: специальные вырожденные случаи (только в треугольнике Шварца (2 2 2)) отмечены большим крестиком. Однородные скрещенные антипризмы с основанием { p }, где p <3/2, не могут существовать, поскольку их вершинные фигуры нарушили бы треугольное неравенство ; они также отмечены большим крестом. 3/2-скрещенная антипризма (трирп) вырождена, плоская в евклидовом пространстве и также отмечена большим крестом. Треугольники Шварца (2 2 n / d ) перечислены здесь только тогда, когда gcd( n , d ) = 1, поскольку в противном случае они приводят только к вырожденным однородным многогранникам.
В списке ниже приведены все возможные случаи, когда n ≤ 6.
| (п q р) | qр | п q.2p.r.2p | пр | д п. 2q.r.2q | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|
| (2 2 2) (м=1) | Х | Х | 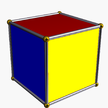 4.4.4 куб 4-п |  3.3.3 тет 2-ап |
| (2 2 3) (м=1) |  4.3.4 путешествие 3-п |  4.3.4 путешествие 3-п | 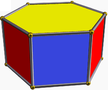 6.4.4 бедро 6-р |  3.3.3.3 октябрь 3-ап |
| (2 2 3/2) (м=2) |  4.3.4 путешествие 3-п |  4.3.4 путешествие 3-п |  6/2.4.4 2 поездки 6/2-п | Х |
| (2 2 4) (м=1) |  4.4.4 куб 4-п |  4.4.4 куб 4-п |  8.4.4 на 8-п |  3.4.3.3 ссориться 4-ап |
| (2 2 4/3) (м=3) |  4.4.4 куб 4-п |  4.4.4 куб 4-п | 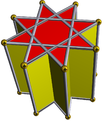 8/3.4.4 останавливаться 8/3-п | Х |
| (2 2 5) (м=1) |  4.5.4 пункт 5-п |  4.5.4 пункт 5-п |  10.4.4 окунать 10-п |  3.5.3.3 папа 5-ап |
| (2 2 5/2) (м=2) |  4.5/2.4 точка 5/2-п |  4.5/2.4 точка 5/2-п |  10/2.4.4 2 пункта 10/2-п |  3.5/2.3.3 шаг 5/2-ап |
| (2 2 5/3) (м=3) |  4.5/2.4 точка 5/2-п |  4.5/2.4 точка 5/2-п |  10/3.4.4 тупик 10/3-п | 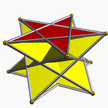 3.5/3.3.3 между 5/3-АП |
| (2 2 5/4) (м=4) |  4.5.4 пункт 5-п |  4.5.4 пункт 5-п |  10/4.4.4 2 шага 10/4-п | Х |
| (2 2 6) (м=1) |  4.6.4 бедро 6-р |  4.6.4 бедро 6-р | 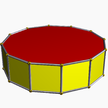 12.4.4 твип 12-п | 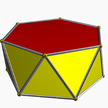 3.6.3.3 случай 6-ап |
| (2 2 6/5) (м=5) |  4.6.4 бедро 6-р |  4.6.4 бедро 6-р |  12/5.4.4 смахнуть 12/5-п | Х |
| (2 2 н ) (м=1) | 4. п .4 н -п | 4. п .4 н -п | 2n2н.4.4 2 н -п | 3. п.3.3 н -ап |
| (2 2 н / д ) (μ= d ) | 4. н / д.4 н / д -п | 4. н / д.4 н / д -п | 2 н / д .4.4 2 н / д -п | 3. н / д .3.3 н / д -ап |
Тетраэдрический
[ редактировать ]В тетраэдрических треугольниках Шварца максимально допустимый числитель равен 3.
| # | (п q р) | д | пиар (пр) д | р | qr (qr) п | р | ПК (кп) р | qр | п q.2p.r.2p | пр | д п. 2q.r.2q | ПК | р 2р.к.2р.п | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (3 3 2) (м=1) |  3.3.3 тет U1 |  3.3.3 тет U1 |  3.3.3.3 октябрь U5 |  3.6.6 tut U2 |  3.6.6 tut U2 |  4.3.4.3 со U7 | 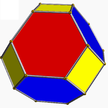 4.6.6 затем U8 | 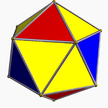 3.3.3.3.3 сила U22 |
| 2 | (3 3 3/2) (м=2) |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  3.6.3/2.6 Проснуться U3 |  3.6.3/2.6 Проснуться U3 |  2(6/2.3.6/2.3) 2 октября – |  2(6/2.6.6) 2тут – |  2(3.3/2.3.3.3.3) 2 октября+8{3} – |
| 3 | (3 2 3/2) (м=3) |  3.3.3.3 октябрь U5 |  3.3.3 тет U1 |  3.3.3 тет U1 |  3.6.6 tut U2 |  2(3/2.4.3.4) 2тах U4* |  3(3.6/2.6/2) 3тет – |  2(6/2.4.6) за+4{6/2} U15* |  3(3.3.3) 3тет – |
| 4 | (2 3/2 3/2) (м=5) |  3.3.3 тет U1 |  3.3.3.3 октябрь U5 |  3.3.3 тет U1 |  3.4.3.4 со U7 |  3(6/2.3.6/2) 3тет – |  3(6/2.3.6/2) 3тет – |  4(6/2.6/2.4) 2 октября+6{4} – |  (3.3.3.3.3)/2 маленький U53 |
| 5 | (3/2 3/2 3/2) (м=6) |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  2(6/2.3.6/2.3) 2 октября – |  2(6/2.3.6/2.3) 2 октября – |  2(6/2.3.6/2.3) 2 октября – |  6(6/2.6/2.6/2) 6 октября – | ? |
Октаэдрический
[ редактировать ]В октаэдрических треугольниках Шварца максимально допустимый числитель равен 4. Также существуют октаэдрические треугольники Шварца, в которых в качестве числа используется 4/2, но это приводит только к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общий делитель .
| # | (п q р) | д | пиар (пр) д | р | qr (qr) п | р | ПК (кп) р | qр | п q.2p.r.2p | пр | д п. 2q.r.2q | ПК | р 2р.к.2р.п | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (4 3 2) (м=1) |  4.4.4 куб U6 |  3.3.3.3 октябрь U5 |  3.4.3.4 со U7 |  3.8.8 тик U9 |  4.6.6 затем U8 |  4.3.4.4 Сирко U10 | 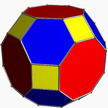 4.6.8 гирко U11 |  3.3.3.3.4 сник U12 |
| 2 | (4 4 3/2) (м=2) |  (3/2.4) 4 окт+6{4} – |  (3/2.4) 4 окт+6{4} – |  (4.4.4.4.4.4)/2 2куба – |  3/2.8.4.8 носок U13 |  3/2.8.4.8 носок U13 |  2(6/2.4.6/2.4) 2co – |  2(6/2.8.8) 2тик – | ? |
| 3 | (4 3 4/3) (м=4) |  (4.4.4.4.4.4)/2 2куба – |  (3/2.4) 4 окт+6{4} – |  (3/2.4) 4 окт+6{4} – |  3/2.8.4.8 носок U13 |  2(4/3.6.4.6) 2чо U15* |  3.8/3.4.8/3 гокко U14 | 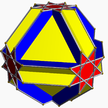 6.8.8/3 Котко U16 | ? |
| 4 | (4 2 3/2) (м=5) |  3.4.3.4 со U7 |  3.3.3.3 октябрь U5 |  4.4.4 куб U6 |  3.8.8 тик U9 |  4.4.3/2.4 хотеть U17 |  4(4.6/2.6/2) 2 октября+6{4} – |  2(4.6/2.8) сро+8{6/2} U18* | ? |
| 5 | (3 2 4/3) (м=7) |  3.4.3.4 со U7 |  4.4.4 куб U6 |  3.3.3.3 октябрь U5 |  4.6.6 затем U8 |  4.4.3/2.4 хотеть U17 |  3.8/3.8/3 ушёл U19 | 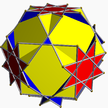 4.6/5.8/3 бросить курить U20 | ? |
| 6 | (2 3/2 4/3) (м=11) |  4.4.4 куб U6 |  3.4.3.4 со U7 |  3.3.3.3 октябрь U5 |  4.3.4.4 Сирко U10 |  4(4.6/2.6/2) 2 октября+6{4} – |  3.8/3.8/3 ушёл U19 |  2(4.6/2.8/3) Гро+8{6/2} U21* | ? |
| 7 | (3/2 4/3 4/3) (м=14) |  (3/2.4) 4 = (3.4) 4 /3 окт+6{4} – |  (4.4.4.4.4.4)/2 2куба – |  (3/2.4) 4 = (3.4) 4 /3 окт+6{4} – |  2(6/2.4.6/2.4) 2co – |  3.8/3.4.8/3 гокко U14 |  3.8/3.4.8/3 гокко U14 |  2(6/2.8/3.8/3) 2выйти – | ? |
икосаэдрический
[ редактировать ]В икосаэдрических треугольниках Шварца максимально допустимый числитель равен 5. Кроме того, числитель 4 вообще нельзя использовать в икосаэдрических треугольниках Шварца, хотя числители 2 и 3 разрешены. (Если бы 4 и 5 могли встретиться вместе в каком-нибудь треугольнике Шварца, они должны были бы встретиться и в каком-нибудь треугольнике Мёбиуса; но это невозможно, поскольку (2 4 5) — гиперболический треугольник, а не сферический.)
| # | (п q р) | д | пиар (пр) д | р | qr (qr) п | р | ПК (кп) р | qр | п q.2p.r.2p | пр | д п. 2q.r.2q | ПК | р 2р.к.2р.п | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (5 3 2) (м=1) |  5.5.5 лань U23 |  3.3.3.3.3 сила U22 |  3.5.3.5 идентификатор U24 |  3.10.10 время U26 |  5.6.6 из U25 |  4.3.4.5 срид U27 | 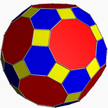 4.6.10 сетка U28 |  3.3.3.3.5 snid U29 |
| 2 | (3 3 5/2) (м=2) |  3.5/2.3.5/2.3.5/2 юбка U30 |  3.5/2.3.5/2.3.5/2 юбка U30 |  (3 10 )/2 2ike – |  3.6.5/2.6 шелк U31 |  3.6.5/2.6 шелк U31 |  2(10/2.3.10/2.3) 2id – |  2(10/2.6.6) 2ти – |  3.5/2.3.3.3.3 см. страницу U32 |
| 3 | (5 5 3/2) (м=2) |  (5.3/2) 5 Сид – |  (5.3/2) 5 Сид – |  (5.5.5.5.5.5)/2 2 олени – |  5.10.3/2.10 осадил U33 |  5.10.3/2.10 осадил U33 |  2(6/2.5.6/2.5) 2id – |  2(6/2.10.10) 2 часа дня – |  2(3.3/2.3.5.3.5) 2id+40{3} – |
| 4 | (5 5/2 2) (м=3) |  (5.5.5.5.5)/2 гад U35 |  5/2.5/2.5/2.5/2.5/2 партизаны U34 |  5/2.5.5/2.5 делал U36 |  5/2.10.10 приходить U37 |  5.10/2.10/2 3 олени – |  4.5/2.4.5 радед U38 |  2(4.10/2.10) сердце+12{10/2} U39* |  3.3.5/2.3.5 Сиддид U40 |
| 5 | (5 3 5/3) (м=4) |  5.5/3.5.5/3.5.5/3 сделал U41 |  (3.5/3) 5 кислотный – |  (3.5) 5 /3 Сид – |  3.10.5/3.10 Сиддит сделал U43 |  5.6.5/3.6 одинаковый U44 |  10/3.3.10/3.5 Гиддит сделал U42 |  10/3.6.10 не знаю U45 | 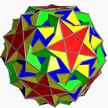 3.5/3.3.3.3.5 односторонний U46 |
| 6 | (5/2 5/2 5/2) (м=6) |  (5/2) 10 /2 2sissid – |  (5/2) 10 /2 2sissid – |  (5/2) 10 /2 2sissid – |  2(5/2.10/2) 2 2 сделал – |  2(5/2.10/2) 2 2 сделал – |  2(5/2.10/2) 2 2 сделал – |  6(10/2.10/2.10/2) 6доу – |  3(3.5/2.3.5/2.3.5/2) 3сидтид – |
| 7 | (5 3 3/2) (м=6) |  (3.5.3.5.3.5)/2 головокружение U47 |  (3 10 )/4 2gike – |  (3.5.3.5.3.5)/2 головокружение U47 |  2(3.10.3/2.10) 2сейхид U49* |  5.6.3/2.6 гид U48 |  5(6/2.3.6/2.5) 3ike+гад – |  2(6.6/2.10) Сидди+20{6/2} U50* |  5(3.3.3.3.3.5)/2 5ike+гад – |
| 8 | (5 5 5/4) (м=6) |  (5 10 )/4 2гад – |  (5 10 )/4 2гад – |  (5 10 )/4 2гад – |  2(5.10.5/4.10) 2сидхид U51* |  2(5.10.5/4.10) 2сидхид U51* |  10/4.5.10/4.5 2 сделал – |  2(10/4.10.10) 2жесткий – |  3(3.5.3.5.3.5) 3cid – |
| 9 | (3 5/2 2) (м=7) |  (3.3.3.3.3)/2 маленький U53 |  5/2.5/2.5/2 гиссид U52 |  5/2.3.5/2.3 гид U54 |  5/2.6.6 Тигги U55 |  3.10/2.10/2 2гад+мощность – |  3(4.5/2.4.3) сикдатрид – |  4.10/2.6 ри+12{10/2} U56* |  3.3.5/2.3.3 госид U57 |
| 10 | (5 5/2 3/2) (м=8) |  (5.3/2) 5 Сид – |  (5/3.3) 5 кислотный – |  5.5/3.5.5/3.5.5/3 сделал U41 |  5/3.10.3.10 Сиддит сделал U43 |  5(5.10/2.3.10/2) сила+3гад – |  3(6/2.5/2.6/2.5) сидтид+гидтид – |  4(6/2.10/2.10) ид+сейхид+сидхид – | ? (3|3 5/2) + (3/2|3 5) |
| 11 | (5 2 5/3) (м=9) |  5.5/2.5.5/2 делал U36 |  5/2.5/2.5/2.5/2.5/2 партизаны U34 |  (5.5.5.5.5)/2 гад U35 |  5/2.10.10 приходить U37 |  3(5.4.5/3.4) каддитрадид – |  10/3.5.5 пусть они остановятся U58 |  10/3.4.10/9 бросил U59 | 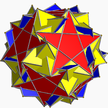 3.5/3.3.3.5 сделал U60 |
| 12 | (3 5/2 5/3) (м=10) |  (3.5/3) 5 кислотный – |  (5/2) 6 /2 2гиссид – |  (5/2.3) 5 /3 кислотный – |  2(5/2.6.5/3.6) 2-сторонний U62* |  3(3.10/2.5/3.10/2) дитдид+гидтид – |  10/3.5/2.10/3.3 Гаддид U61 |  10/3.10/2.6 головокружительный+12{10/2} U63* |  3.5/3.3.5/2.3.3 Гисдид U64 |
| 13 | (5 3 5/4) (м=10) |  (5.5.5.5.5.5)/2 2 олени – |  (3/2.5) 5 Сид – |  (3.5) 5 /3 Сид – |  3/2.10.5.10 осадил U33 |  2(5.6.5/4.6) 2гидхей U65* |  3(10/4.3.10/4.5) sidtid+ditdid – |  2(10/4.6.10) Сидди+12{10/4} U50* | ? |
| 14 | (5 2 3/2) (м=11) |  5.3.5.3 идентификатор U24 |  3.3.3.3.3 сила U22 |  5.5.5 лань U23 |  3.10.10 время U26 |  3(5/4.4.3/2.4) Гидатрид – |  5(5.6/2.6/2) 2ike+гад – |  2(6/2.4.10) сердце+20{6/2} U39* |  5(3.3.3.5.3)/2 4ike+гад – |
| 15 | (3 2 5/3) (м=13) |  3.5/2.3.5/2 гид U54 |  5/2.5/2.5/2 гиссид U52 |  (3.3.3.3.3)/2 маленький U53 |  5/2.6.6 Тигги U55 |  3.4.5/3.4 разрушение U67 |  10/3.10/3.3 выйти из Гиссида U66 |  10/3.4.6 гакватид U68 |  3.5/3.3.3.3 Гис U69 |
| 16 | (5/2 5/2 3/2) (м=14) |  (5/3.3) 5 кислотный – |  (5/3.3) 5 кислотный – |  (5/2) 6 /2 2гиссид – |  3(5/3.10/2.3.10/2) дитдид+гидтид – |  3(5/3.10/2.3.10/2) дитдид+гидтид – |  2(6/2.5/2.6/2.5/2) 2гид – |  10(6/2.10/2.10/2) 2ike+4gad – | ? |
| 17 | (3 3 5/4) (м=14) |  (3.5.3.5.3.5)/2 головокружение U47 |  (3.5.3.5.3.5)/2 головокружение U47 |  (3) 10 /4 2gike – |  3/2.6.5.6 гид U48 |  3/2.6.5.6 гид U48 |  2(10/4.3.10/4.3) 2гид – |  2(10/4.6.6) 2тигги – | ? |
| 18 | (3 5/2 5/4) (м=16) |  (3/2.5) 5 Сид – |  5/3.5.5/3.5.5/3.5 сделал U41 |  (5/2.3) 5 /3 кислотный – |  5/3.6.5.6 одинаковый U44 |  5(3/2.10/2.5.10/2) сила+3гад – |  5(10/4.5/2.10/4.3) 3sissid+гик – |  4(10/4.10/2.6) дид+сидхей+гидхей – | ? |
| 19 | (5/2 2 3/2) (м=17) |  3.5/2.3.5/2 гид U54 |  (3.3.3.3.3)/2 маленький U53 |  5/2.5/2.5/2 гиссид U52 |  5(10/2.3.10/2) 2гад+мощность – |  5/3.4.3.4 разрушение U67 |  5(6/2.6/2.5/2) 2гике+партизаны – |  6(6/2.4.10/2) 2гидтид+ром – | ? |
| 20 | (5/2 5/3 5/3) (м=18) |  (5/2) 10 /2 2sissid – |  (5/2) 10 /2 2sissid – |  (5/2) 10 /2 2sissid – |  2(5/2.10/2) 2 2 сделал – |  2(5/2.10/3.5/3.10/3) 2гидхид U70* |  2(5/2.10/3.5/3.10/3) 2гидхид U70* |  2(10/3.10/3.10/2) 2бросить партизан – | ? |
| 21 | (3 5/3 3/2) (м=18) |  (3 10 )/2 2ike – |  5/2.3.5/2.3.5/2.3 юбка U30 |  5/2.3.5/2.3.5/2.3 юбка U30 |  5/2.6.3.6 шелк U31 |  2(3.10/3.3/2.10/3) 2 гея U71* |  5(6/2.5/3.6/2.3) партизаны+3жик – |  2(6/2.10/3.6) головокружительный+20{6/2} U63* | ? |
| 22 | (3 2 5/4) (м=19) |  3.5.3.5 идентификатор U24 |  5.5.5 лань U23 |  3.3.3.3.3 сила U22 |  5.6.6 из U25 |  3(3/2.4.5/4.4) Гидатрид – |  5(10/4.10/4.3) 2sissid+гик – |  2(10/4.4.6) ри+12{10/4} U56* | ? |
| 23 | (5/2 2 5/4) (м=21) |  5/2.5.5/2.5 делал U36 |  (5.5.5.5.5)/2 гад U35 |  5/2.5/2.5/2.5/2.5/2 партизаны U34 |  3(10/2.5.10/2) 3 олени – |  3(5/3.4.5.4) каддитрадид – |  3(10/4.5/2.10/4) 3гиссид – |  6(10/4.4.10/2) 2ditdid+ром – | ? |
| 24 | (5/2 3/2 3/2) (м=22) |  5/2.3.5/2.3.5/2.3 юбка U30 |  (3 10 )/2 2ike – |  5/2.3.5/2.3.5/2.3 юбка U30 |  2(3.10/2.3.10/2) 2id – |  5(5/3.6/2.3.6/2) партизаны+3жик – |  5(5/3.6/2.3.6/2) партизаны+3жик – |  10(6/2.6/2.10/2) 4ike+2gad – | 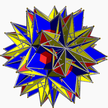 (3.3.3.3.3.5/2)/2 сэрсид U72 |
| 25 | (2 5/3 3/2) (м=23) |  (3.3.3.3.3)/2 маленький U53 |  5/2.3.5/2.3 гид U54 |  5/2.5/2.5/2 гиссид U52 |  3(5/2.4.3.4) сикдатрид – |  10/3.3.10/3 выйти из Гиссида U66 |  5(6/2.5/2.6/2) 2гике+партизаны – |  2(6/2.10/3.4) пояс+20{6/2} U73* |  (3.3.3.5/2.3)/2 гирсид U74 |
| 26 | (5/3 5/3 3/2) (м=26) |  (5/2.3) 5 /3 кислотный – |  (5/2.3) 5 /3 кислотный – |  (5/2) 6 /2 2гиссид – |  5/2.10/3.3.10/3 Гаддид U61 |  5/2.10/3.3.10/3 Гаддид U61 |  2(6/2.5/2.6/2.5/2) 2гид – |  2(6/2.10/3.10/3) 2quitgissid – | ? |
| 27 | (2 5/3 5/4) (м=27) |  (5.5.5.5.5)/2 гад U35 |  5/2.5.5/2.5 делал U36 |  5/2.5/2.5/2.5/2.5/2 партизаны U34 |  5/2.4.5.4 радед U38 |  10/3.5.10/3 пусть они остановятся U58 |  3(10/4.5/2.10/4) 3гиссид – |  2(10/4.10/3.4) пояс+12{10/4} U73* | ? |
| 28 | (2 3/2 5/4) (м=29) |  5.5.5 лань U23 |  3.5.3.5 идентификатор U24 |  3.3.3.3.3 сила U22 |  3.4.5.4 срид U27 |  2(6/2.5.6/2) 2ike+гад – |  5(10/4.3.10/4) 2sissid+гик – |  6(10/4.6/2.4/3) 2сидтид+ром – | ? |
| 29 | (5/3 3/2 5/4) (м=32) |  5/3.5.5/3.5.5/3.5 сделал U41 |  (3.5) 5 /3 Сид – |  (3.5/2) 5 /3 кислотный – |  3.10/3.5.10/3 Гиддит сделал U42 |  3(5/2.6/2.5.6/2) сидтид+гидтид – |  5(10/4.3.10/4.5/2) 3sissid+гик – |  4(10/4.6/2.10/3) гид+гейхид+гидхид – | ? |
| 30 | (3/2 3/2 5/4) (м=34) |  (3.5.3.5.3.5)/2 головокружение U47 |  (3.5.3.5.3.5)/2 головокружение U47 |  (3) 10 /4 2gike – |  5(3.6/2.5.6/2) 3ike+гад – |  5(3.6/2.5.6/2) 3ike+гад – |  2(10/4.3.10/4.3) 2гид – |  10(10/4.6/2.6/2) 2sissid+4gike – | ? |
| 31 | (3/2 5/4 5/4) (м=38) |  (3.5) 5 /3 Сид – |  (5.5.5.5.5.5)/2 2 олени – |  (3.5) 5 /3 Сид – |  2(5.6/2.5.6/2) 2id – |  3(3.10/4.5/4.10/4) sidtid+ditdid – |  3(3.10/4.5/4.10/4) sidtid+ditdid – |  10(10/4.10/4.6/2) 4сиссид+2гике – |  5(3.3.3.5/4.3.5/4) 4ike+2gad – |
| 32 | (5/4 5/4 5/4) (м=42) |  (5) 10 /4 2гад – |  (5) 10 /4 2гад – |  (5) 10 /4 2гад – |  2(5.10/4.5.10/4) 2 сделал – |  2(5.10/4.5.10/4) 2 сделал – |  2(5.10/4.5.10/4) 2 сделал – |  6(10/4.10/4.10/4) 2гиссид – |  3(3/2.5.3/2.5.3/2.5) 3cid – |
Невитоффианский
[ редактировать ]Геми формы
[ редактировать ]Помимо октагемиоктаэдра , полумногогранники генерируются как двойные покрытия с помощью конструкции Витгофа. [3]
 3/2.4.3.4 вот это U4 полу(3 3/2 | 2) |  4/3.6.4.6 давать U15 полу(4 4/3 | 3) |  5/4.10.5.10 Сидхид U51 полу(5 5/4 | 5) |  5/2.6.5/3.6 Сидхей U62 полу(5/2 5/3 | 3) |  5/2.10/3.5/3.10/3 гид U70 полу(5/2 5/3 | 5/3) |
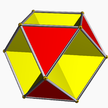 3/2.6.3.6 Проснуться U3 геми(?) |  3/2.10.3.10 шейхи U49 полу(3 3/2 | 5) |  5.6.5/4.6 головокружительный U65 полу(5 5/4 | 3) |  3.10/3.3/2.10/3 прибытие U71 полу(3 3/2 | 5/3) |
Уменьшенные формы
[ редактировать ]Эти многогранники создаются с дополнительными гранями с помощью конструкции Витхоффа.
| Витхофф | Многогранник | Дополнительные лица | Витхофф | Многогранник | Дополнительные лица | Витхофф | Многогранник | Дополнительные лица | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 2 3/2 | |  4.6.4/3.6 давать U15 | 4{6/2} | 4 2 3/2 | |  4.8.4/3.8/7 сро U18 | 8{6/2} | 2 3/2 4/3 | |  4.8/3.4/3.8/5 Грох U21 | 8{6/2} | ||
| 5 5/2 2 | |  4.10.4/3.10/9 сердце U39 | 12{10/2} | 5 3 3/2 | |  10.6.10/9.6/5 Сидди U50 | 20{6/2} | 3 5/2 2 | |  6.4.6/5.4/3 ри U56 | 12{10/2} | ||
| 5 5/2 3/2 | |  3/2.10.3.10 шейхи U49 | ид + сидхид | 5 5/2 3/2 | |  5/4.10.5.10 Сидхид U51 | идентификатор + сехид | 5 3 5/4 | |  10.6.10/9.6/5 Сидди U50 | 12{10/4} | ||
| 3 5/2 5/3 | |  6.10/3.6/5.10/7 головокружительный U63 | 12{10/2} | 5 2 3/2 | |  4.10/3.4/3.10/9 сердце U39 | 20{6/2} | 3 5/2 5/4 | |  5.6.5/4.6 головокружительный U65 | сделал + Сидхей | ||
| 3 5/2 5/4 | |  5/2.6.5/3.6 Сидхей U62 | сделал + гидхей | 3 5/3 3/2 | |  6.10/3.6/5.10/7 головокружительный U63 | 20{6/2} | 3 2 5/4 | |  6.4.6/5.4/3 ри U56 | 12{10/4} | ||
| 2 5/3 3/2 | |  4.10/3.4/3.10/7 препоясывать U73 | 20{6/2} | 5/3 3/2 5/4 | |  3.10/3.3/2.10/3 прибытие U71 | действительно + действительно | 5/3 3/2 5/4 | |  5/2.10/3.5/3.10/3 гид U70 | гид + гейхид | ||
| 2 5/3 5/4 | |  4.10/3.4/3.10/7 препоясывать U73 | 12{10/4} |
Тетрагемигексаэдр . (thah, U4) также является уменьшенной версией {3/2} -купола (ретроградного треугольного купола, ratricu) на {6/2} Таким образом, его также можно назвать скрещенным треугольным куплоидом .
Многие приведенные выше случаи получены из вырожденных всеусеченных многогранников pqr |. В этих случаях возможны два различных вырожденных случая pqr | и ПК | может быть сгенерировано из одних и тех же p и q; результат имеет грани {2p}, {2q} и совпадающие грани {2r} или {2s} соответственно. Оба они дают одни и те же невырожденные однородные многогранники, если отбросить совпадающие грани, которые Коксетер символизировал pq р
с |. Эти случаи перечислены ниже:
 4.6.4/3.6 давать U15 2 3 3/2 3/2 | |  4.8.4/3.8/7 сро U18 2 3 3/2 4/2 | |  4.10.4/3.10/9 сердце U39 2 3 3/2 5/2 | |  6.10/3.6/5.10/7 головокружительный U63 3 5/3 3/2 5/2 | |
 6.4.6/5.4/3 ри U56 2 3 5/4 5/2 | |  4.8/3.4/3.8/5 Грох U21 2 4/3 3/2 4/2 | |  4.10/3.4/3.10/7 препоясывать U73 2 5/3 3/2 5/4 | |  10.6.10/9.6/5 Сидди U50 3 5 3/2 5/4 | |
В малых и больших ромбогексаэдрах используется дробь 4/2, несмотря на то, что она не является наименьшей. Пока 2 4 2 | и 2 4/3 2 | представляют собой одну восьмиугольную или октаграммную призму соответственно, 2 4 4/2 | и 2 4/3 4/2 | представляют собой три такие призмы, некоторые из которых имеют общие квадратные грани (именно те, которые сложены вдвое, образуя {8/2}). Эти {8/2} имеют четырехкратную, а не двукратную вращательную симметрию, что оправдывает использование 4/2 вместо 2. [2]
Другие формы
[ редактировать ]Эти два однородных многогранника вообще не могут быть порождены конструкцией Витгофа. Это набор однородных многогранников, которые обычно называют «не-витоффианами». Вместо треугольных фундаментальных областей однородных многогранников Витгофа эти два многогранника имеют тетрагональные фундаментальные области.
Фигуре Скиллинга не присвоен индекс в списке Мэдера, поскольку она представляет собой экзотический однородный многогранник с полностью совпадающими гребнями (ребрами в трехмерном случае). Это также верно в отношении некоторых вырожденных многогранников, включенных в приведенный выше список, таких как небольшой комплексный икосододекаэдр . Такая интерпретация совпадения ребер позволяет этим фигурам иметь две грани на каждое ребро: если не удвоить ребра, у них будет 4, 6, 8, 10 или 12 граней, встречающихся на ребре, фигуры, которые обычно исключаются как однородные многогранники. Фигура Скиллинга состоит из четырех граней, сходящихся по краям.
| (pqrs) | | pqrs (4.п. 4.q.4.r.4.s)/2 | | (р) д (г) с (п 3 .4.q.4.r 3 .4.с.4)/2 |
|---|---|---|
| (3/2 5/3 3 5/2) |  (4.3/2.4.5/3.4.3.4.5/2)/2 gidrid U75 | 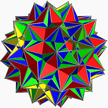 (3/2 3 .4.5/3.4.3 3 .4.5/2.4)/2 гидисдрид навыки |
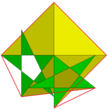 Вершинная фигура | 3 5/3 5/2 |  Большой курносый додецикосододекаэдр |  Большой диромбикосидодекаэдр |  Вершинная фигура | 3/2 5/3 3 5/2 |
 Большой диснуб диромбидодекаэдр |  Соединение двадцати октаэдров |  Соединение двадцати тетрагемигексаэдров. |  Вершинная фигура |(3/2) 5/3 (3) 5/2 |
Оба этих особых многогранника могут происходить от большого курносого додецикосододекаэдра | 3 5/3 5/2 (U64). Это хиральный курносый многогранник, но его пентаграммы расположены в компланарных парах. Объединив одну копию этого многогранника с его энантиоморфом, пентаграммы совпадают и могут быть удалены. Поскольку ребра вершинной фигуры этого многогранника включают в себя три стороны квадрата, причем четвертая сторона представляет собой его энантиоморф, мы видим, что полученный многогранник на самом деле представляет собой соединение двадцати октаэдров . Каждый из этих октаэдров содержит одну пару параллельных граней, образующих полностью симметричный треугольник | 3 5/3 5/2, а остальные три взяты из оригинала | Курносые треугольники 3 5/3 5/2. Кроме того, каждый октаэдр можно заменить тетраполушестигранником с такими же ребрами и вершинами. Взяв полностью симметричные треугольники в октаэдрах, исходные совпадающие пентаграммы в больших курносых додецикосододекаэдрах и экваториальные квадраты тетрагемигексаэдров вместе, мы получим большой диромбикосидодекаэдр (монстр Миллера). [2] Взяв вместо этого курносые треугольники октаэдров, мы получим большой неспусковой диромбидодекаэдр (фигура Скиллинга). [4]
Евклидовы мозаики
[ редактировать ]Единственные плоские треугольники, которые перекрывают плоскость один раз, - это (3 3 3), (4 2 4) и (3 2 6): это соответственно равносторонний треугольник, прямоугольный равнобедренный треугольник 45-45-90 и треугольник 30°. -60-90 прямоугольный треугольник. Отсюда следует, что любой плоский треугольник, замостивший плоскость несколько раз, должен быть составлен из нескольких копий одного из них. Единственная возможность - это тупо равнобедренный треугольник 30-30-120 (3/2 6 6) = (6 2 3) + (2 6 3), дважды перекрывающий плоскость. Каждый треугольник считается дважды с противоположной ориентацией, с точкой ветвления в вершинах 120 °. [5]
Замощение {∞,2}, составленное из двух апейрогонов, не принимается, поскольку его грани сходятся более чем на одном ребре. Здесь ∞' обозначает ретроградный аналог ∞.
Вырожденные именованные формы:
- хатит: соединение трех шестиугольных плиток + треугольная мозаика
- чата: соединение трех шестиугольных мозаик + треугольная мозаика + двойные покрытия апейрогонов вдоль всех реберных последовательностей.
- cha: соединение трех шестиугольных мозаик + двойные покрытия апейрогонов вдоль всех реберных последовательностей.
- cosa: квадратная мозаика + двойные покрытия апейрогонов вдоль всех реберных последовательностей
| (п q р) | д | пиар (пр) д | р | qr (qr) п | р | ПК (кп) р | qр | п q.2p.r.2p | пр | д п.2q.r.2q | ПК | р 2р.к.2р.п | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|
| (6 3 2) |  6.6.6 гексат |  3.3.3.3.3.3 шагнул |  3.6.3.6 что |  3.12.12 отравленный |  6.6.6 гексат |  4.3.4.6 сроэто |  4.6.12 Грот это |  3.3.3.3.6 снатхат |
| (4 4 2) |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.8.8 тосковать |  4.8.8 тосковать |  4.4.4.4 приседать |  4.8.8 тосковать |  3.3.4.3.4 приседать |
| (3 3 3) |  3.3.3.3.3.3 шагнул |  3.3.3.3.3.3 шагнул |  3.3.3.3.3.3 шагнул |  3.6.3.6 что |  3.6.3.6 что |  3.6.3.6 что |  6.6.6 гексат |  3.3.3.3.3.3 шагнул |
| (∞ 2 2) | — | — | — | — |  4.4.∞ zip |  4.4.∞ zip |  4.4.∞ zip | 3.3.3.∞ мучить |
| (3/2 3/2 3) |  3.3.3.3.3.3 шагнул |  3.3.3.3.3.3 шагнул |  3.3.3.3.3.3 шагнул | ∞-покрытый {3} | ∞-покрытый {3} |  3.6.3.6 что | [дегенерат] | ? |
| (4 4/3 2) |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.8.8 тосковать |  4.8/5.8/5 бросить приседать | ∞-покрытый {4} |  4.8/3.8/7 падает | ? |
| (4/3 4/3 2) |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.4.4.4 приседать |  4.8/5.8/5 бросить приседать |  4.8/5.8/5 бросить приседать |  4.4.4.4 приседать |  4.8/5.8/5 бросить приседать |  3.3.4/3.3.4/3 расискват |
| (3/2 6 2) |  3.3.3.3.3.3 шагнул |  6.6.6 гексат |  3.6.3.6 что | [дегенерат] |  3.12.12 отравленный |  3/2.4.6/5.4 qrothat | [дегенерат] | ? |
| (3 6/5 2) |  3.3.3.3.3.3 шагнул |  6.6.6 гексат |  3.6.3.6 что |  6.6.6 гексат |  3/2.12/5.12/5 цитирую это |  3/2.4.6/5.4 qrothat |  4.6/5.12/5 бросить это | ? |
| (3/2 6/5 2) |  3.3.3.3.3.3 шагнул |  6.6.6 гексат |  3.6.3.6 что | [дегенерат] |  3/2.12/5.12/5 цитирую это |  3.4.6.4 сроэто | [дегенерат] | ? |
| (3/2 6 6) |  (3/2.6) 6 чаты |  (6.6.6.6.6.6)/2 2 шестнадцатеричных |  (3/2.6) 6 чаты | [дегенерат] |  3/2.12.6.12 выстрел |  3/2.12.6.12 выстрел | [дегенерат] | ? |
| (3 6 6/5) |  (3/2.6) 6 чаты |  (6.6.6.6.6.6)/2 2 шестнадцатеричных |  (3/2.6) 6 чаты | ∞-покрытый {6} |  3/2.12.6.12 выстрел |  3.12/5.6/5.12/5 иди это |  6.12/5.12/11 ты говоришь | ? |
| (3/2 6/5 6/5) |  (3/2.6) 6 чаты |  (6.6.6.6.6.6)/2 2 шестнадцатеричных |  (3/2.6) 6 чаты | [дегенерат] |  3.12/5.6/5.12/5 иди это |  3.12/5.6/5.12/5 иди это | [дегенерат] | ? |
| (3 3/2 ∞) |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое | — |  6.3/2.6.∞ коттедж | [дегенерат] |  3.∞.3/2.∞ Да | [дегенерат] | ? |
| (3 3 ∞') |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое | — |  6.3/2.6.∞ коттедж |  6.3/2.6.∞ коттедж | [дегенерат] | [дегенерат] | ? |
| (3/2 3/2 ∞') |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое |  (3.∞) 3 /2 = (3/2.∞) 3 то же самое | — | [дегенерат] | [дегенерат] | [дегенерат] | [дегенерат] | ? |
| (4 4/3 ∞) |  (4.∞) 4 /3 Что |  (4.∞) 4 /3 Что | — |  8.4/3.8.∞ сука |  8/3.4.8/3.∞ Сосса |  4.∞.4/3.∞ напиток |  8.8/3.∞ инвестировать |  3.4.3.4/3.3.∞ в снегу |
| (4 4 ∞') |  (4.∞) 4 /3 Что |  (4.∞) 4 /3 Что | — |  8.4/3.8.∞ сука |  8.4/3.8.∞ сука | [дегенерат] | [дегенерат] | ? |
| (4/3 4/3 ∞') |  (4.∞) 4 /3 Что |  (4.∞) 4 /3 Что | — |  8/3.4.8/3.∞ Сосса |  8/3.4.8/3.∞ Сосса | [дегенерат] | [дегенерат] | ? |
| (6 6/5 ∞) |  (6.∞) 6 /5 нет |  (6.∞) 6 /5 нет | — |  6/5.12.∞.12 гхаха |  6.12/5.∞.12/5 shaha |  6.∞.6/5.∞ 2хоха |  12.12/5.∞ хатха | ? |
| (6 6 ∞') |  (6.∞) 6 /5 нет |  (6.∞) 6 /5 нет | — |  6/5.12.∞.12 гхаха |  6/5.12.∞.12 гхаха | [дегенерат] | [дегенерат] | ? |
| (6/5 6/5 ∞') |  (6.∞) 6 /5 нет |  (6.∞) 6 /5 нет | — |  6.12/5.∞.12/5 shaha |  6.12/5.∞.12/5 shaha | [дегенерат] | [дегенерат] | ? |
Плитка 6 6/5 | ∞ генерируется как двойное накрытие по конструкции Витхоффа:
 6.∞.6/5.∞ скучный полу(6 6/5 | ∞) |
Также есть несколько тайлингов со смешанным символом pq. р
с |:
 4.12.4/3.12/11 шрахт 2 6 3/2 3 | |  4.12/5.4/3.12/7 Грахат 2 6/5 3/2 3 | |  8/3.8.8/5.8/7 sost 4/3 4 2 ∞ | |  12/5.12.12/7.12/11 да 6/5 6 3 ∞ | |
Есть также некоторые невитоффовы мозаики:
 3.3.3.4.4 этрат | 3.3.3.4/3.4/3 портрет |
Полнота множества однородных разбиений плоскости не доказана, в отличие от множества однородных многогранников. Вышеуказанные мозаики представляют собой все мозаики, найденные Кокстером, Лонге-Хиггинсом и Миллером в их статье 1954 года об однородных многогранниках. Они предположили, что списки полны: это было доказано Соповым в 1970 году для однородных многогранников, но не доказано для однородных мозаик. Действительно, Бранко Грюнбаум , Дж. К. Миллер и Дж. К. Шепард перечисляют еще пятнадцать не-Витоффовых однородных мозаик в книге «Равномерные мозаики с полыми плитками» (1981): [6]
Для фигур вершин 4.8.4/3.8.4/3.∞ и 4.8/3.4.8/3.4/3.∞ имеется по два мозаики; они используют одни и те же наборы вершин и ребер, но имеют другой набор квадратов. Существует также третья мозаика для каждой из этих двух вершинных фигур, которая является лишь псевдооднородной (все вершины выглядят одинаково, но находятся на двух орбитах симметрии). Следовательно, для евклидовых мозаик конфигурация вершин не определяет однозначно мозаику. [6] На рисунках ниже входящие в комплект квадраты с горизонтальными и вертикальными краями отмечены центральной точкой. У одного квадрата края выделены. [6]
- Униформа ( группа обоев п4м)
- Униформа (группа обоев p4g)
- Псевдо-униформа
Грюнбаум, Миллер и Шепард также перечисляют 33 однородных мозаики, использующих зигзаги (косые апейрогоны) в качестве граней, десять из которых представляют собой семейства, имеющие свободный параметр (угол зигзага). В восьми случаях этот параметр является непрерывным; в двух случаях он дискретен. [6]
Гиперболические мозаики
[ редактировать ]Множество треугольников, замощающих гиперболическую плоскость, бесконечно. Более того, в гиперболическом пространстве фундаментальная область не обязательно должна быть симплексом. Следовательно, полный список равномерных разбиений гиперболической плоскости дать невозможно.
Даже если ограничиться выпуклыми плитками, можно найти несколько плиток с одинаковой конфигурацией вершин: см., например, квадратную плитку Snub порядка 6#Связанные многогранники и мозаику . [7]
Ниже приведены несколько небольших выпуклых случаев (без идеальных граней или вершин):
| (п q р) | д | пиар (пр) д | р | qr (qr) п | р | ПК (кп) р | qр | п q.2p.r.2p | пр | д п.2q.r.2q | ПК | р 2р.к.2р.п | пкр | 2р.2д.2п | | пкр 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|
| (7 3 2) |  7.7.7 нагревать |  3.3.3.3.3.3.3 взволнованный |  3.7.3.7 тогда |  3.14.14 театр |  6.6.7 тетрат |  4.3.4.7 мучить |  4.6.14 грот |  3.3.3.3.7 снатет |
| (8 3 2) |  8.8.8 уксус |  3.3.3.3.3.3.3.3 отрат |  3.8.3.8 ток |  3.16.16 фарш |  6.6.8 тотрат |  4.3.4.8 сротокт |  4.6.16 грот |  3.3.3.3.8 снатокт |
| (5 4 2) |  5.5.5.5 торф |  4.4.4.4.4 рыба |  4.5.4.5 теплый |  4.10.10 торф |  5.8.8 топесет |  4.4.4.5 туалетный лоток |  4.8.10 Гротепет |  3.3.4.3.5 степи |
| (6 4 2) |  6.6.6.6 шексат |  4.4.4.4.4.4 Это |  4.6.4.6 могу сделать |  4.12.12 тошексат |  6.8.8 этоткват |  4.4.4.6 сротехат |  4.8.12 большая шляпа |  3.3.4.3.6 змеиная шляпа |
| (5 5 2) |  5.5.5.5.5 тугой |  5.5.5.5.5 тугой |  5.5.5.5 торф |  5.10.10 топепат |  5.10.10 топепат |  4.5.4.5 теплый |  4.10.10 торф |  3.3.5.3.5 спепат |
| (6 6 2) |  6.6.6.6.6.6 рукава |  6.6.6.6.6.6 рукава |  6.6.6.6 шексат |  6.12.12 эта шляпа |  6.12.12 эта шляпа |  4.6.4.6 могу сделать |  4.12.12 тошексат |  3.3.6.3.6 шихат |
| (4 3 3) |  3.4.3.4.3.4 дитититекэт |  3.3.3.3.3.3.3.3 отрат |  3.4.3.4.3.4 дитититекэт |  3.8.3.8 ток |  6.3.6.4 сидеть титрованным |  6.3.6.4 сидеть титрованным |  6.6.8 тотрат |  3.3.3.3.3.4 останавливаться |
| (4 4 3) |  3.4.3.4.3.4.3.4 дитететрат |  3.4.3.4.3.4.3.4 дитететрат |  4.4.4.4.4.4 Это |  4.8.3.8 сидячие чаи |  4.8.3.8 сидячие чаи |  6.4.6.4 могу сделать |  6.8.8 этоткват |  3.3.3.4.3.4 название |
| (4 4 4) |  4.4.4.4.4.4.4.4 целовать |  4.4.4.4.4.4.4.4 целовать |  4.4.4.4.4.4 целовать |  4.8.4.8 теокт |  4.8.4.8 теокт |  4.8.4.8 теокт |  8.8.8 уксус |  3.4.3.4.3.4 дитититекэт |
Ссылки
[ редактировать ]- ^ Акронимы Бауэрса для однородных многогранников приведены в книге Р. Клитцинга, Осесимметричные грани однородных многогранников , Симметрия: Культура и наука, Том. 13, № 3-4, 241-258, 2002 г.
- ^ Jump up to: а б с Коксетер, 1954 год.
- ^ Явно указано для тетрагемигексаэдра в Coxeter et al. 1954, стр. 415–6.
- ^ Скиллинг, 1974 г.
- ^ Коксетер, Правильные многогранники , с. 114
- ^ Jump up to: а б с д Грюнбаум, Бранко; Миллер, JCP; Шепард, GC (1981). «Равномерная черепица с полыми плитками». В Дэвисе, Чендлер; Грюнбаум, Бранко; Шерк, Ф.А. (ред.). Геометрическая жилка: Фестиваль Коксетера . Спрингер. стр. 17–64. ISBN 978-1-4612-5650-2 .
- ^ Полуправильные мозаики гиперболической плоскости , Басудеб Датта и Субходжой Гупта
- Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки . 246 (916). Королевское общество: 401–450. дои : 10.1098/rsta.1954.0003 . ISSN 0080-4614 . JSTOR 91532 . МР 0062446 . S2CID 202575183 . [1]
- Скиллинг, Дж. (1974). «Полное множество однородных многогранников». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки . 278 (1278). Королевское общество: 111–135. дои : 10.1098/rsta.1975.0022 . ISSN 1364-503X . S2CID 122634260 . [2]
Ричард Клитцинг: Многогранники
- симметрия точечной группы
- сложность
- Треугольники Шварца часть 1 , часть 2
- Евклидовы мозаики и соты
- Гиперболические мозаики и соты
Таблицы основаны на таблицах, представленных Клитцингом на его сайте.
Внешние ссылки
[ редактировать ]Джим Макнил:
Цви Хар’Эл:
Хиронори Сакамото:















