Малый ретровзносый икосикосододекаэдр

Малый ретровзносый икосикосододекаэдр

Тип	Однородный звездчатый многогранник
Элементы	Ф = 112, Е = 180 V = 60 (χ = −8)
Лица по сторонам	(40+60){3}+12{5/2}
Диаграмма Кокстера
Символ Витхоффа	\| 3/2 3/2 5/2
Группа симметрии	I _h, [5,3], *532
Ссылки на индексы	Ю ₇₂ , С ₉₁ , Ж ₁₁₈
Двойной многогранник	Малый гексаграммный гексеконтаэдр
Вершинная фигура	(3 ⁵.5/3)/2
Аббревиатура Бауэрса	Сирсид

В геометрии малый ретроносый икосикосододекаэдр (также известный как ретроносый дисикосидодекаэдр , малый перевернутый ретроносый икосикосододекаэдр или ретроголосносый икосаэдр ) представляет собой невыпуклый однородный многогранник , обозначаемый как $U 72$ . У него 112 граней (100 треугольников и 12 пентаграмм ), 180 ребер и 60 вершин. ^[1] Дан символ Шлефли sr{⁵/₃,³/₂}.

40 несносых треугольных граней образуют 20 компланарных пар, образуя звездчатые шестиугольники не совсем правильные . В отличие от большинства курносых многогранников, он обладает отражательной симметрией.

Георгий Ольшевский прозвал его йог-сототом (в честь божества мифов Ктулху ). ^[2]^[3]

Выпуклая оболочка

Его выпуклая оболочка представляет собой неоднородный усеченный додекаэдр .

Усеченный додекаэдр	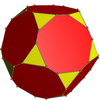Выпуклая оболочка	Малый ретровзносый икосикосододекаэдр

Декартовы координаты

Позволять $\xi =-{\frac {3}{2}}-{\frac {1}{2}}{\sqrt {1+4\phi }}\approx -2.866760399173862$ быть наименьшим (самым отрицательным) нулем многочлена $P=x^{2}+3x+\phi ^{-2}$ , где $\phi$ это золотое сечение . Пусть точка $p$ быть предоставлено

p={\begin{pmatrix}\phi ^{-1}\xi +\phi ^{-3}\\\xi \\\phi ^{-2}\xi +\phi ^{-2}\end{pmatrix}}

.

Пусть матрица $M$ быть предоставлено

M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}

.

$M$ это вращение вокруг оси $(1,0,\phi )$ под углом $2\pi /5$ , против часовой стрелки. Пусть линейные преобразования $T_{0},\ldots ,T_{11}$ быть преобразованиями, которые посылают точку $(x,y,z)$ к четным перестановкам $(\pm x,\pm y,\pm z)$ с четным количеством знаков минус. Преобразования $T_{i}$ составляют группу вращательных симметрий правильного тетраэдра .Преобразования $T_{i}M^{j}$ $(i=0,\ldots ,11$ , $j=0,\ldots ,4)$ составляют группу вращательных симметрий правильного икосаэдра .Тогда 60 баллов $T_{i}M^{j}p$ являются вершинами небольшого курносого икосикосидодекаэдра. Длина ребра равна $-2\xi$ , радиус описанной окружности равен ${\sqrt {-4\xi -\phi ^{-2}}}$ , а средний радиус равен ${\sqrt {-\xi }}$ .

Для небольшого курносого икосикосидодекаэдра, длина ребра которого равна 1,радиус описанной окружности

R={\frac {1}{2}}{\sqrt {\frac {\xi -1}{\xi }}}\approx 0.5806948001339209

Его средний радиус

r={\frac {1}{2}}{\sqrt {\frac {-1}{\xi }}}\approx 0.2953073837589815

Другой ноль $P$ аналогичную роль играет в описании малого курносого икосикосододекаэдра .

См. также

Ссылки

^ Медер, Роман. «72: малый ретроносый икосикосододекаэдр» . МатКонсалт .
^ Биррелл, Роберт Дж. (май 1992 г.). Йог-сотот: анализ и построение небольшого перевернутого ретроносого икосикосидодекаэдра (MS). Калифорнийский государственный университет.
^ Бауэрс, Джонатан (2000). «Равномерная Полихора» (PDF) . В Резе Сархаги (ред.). Мосты 2000 . Конференция по мостам. стр. 239–246.

Внешние ссылки

Вайсштейн, Эрик В. «Маленький ретроносый икосикосододекаэдр» . Математический мир .
Клитцинг, Ричард. «3D звезда малый ретроносый икосикосидодекаэдр» .

Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее .

[1] Медер, Роман. «72: малый ретроносый икосикосододекаэдр» . МатКонсалт .

[2] Биррелл, Роберт Дж. (май 1992 г.). Йог-сотот: анализ и построение небольшого перевернутого ретроносого икосикосидодекаэдра (MS). Калифорнийский государственный университет.

[3] Бауэрс, Джонатан (2000). «Равномерная Полихора» (PDF) . В Резе Сархаги (ред.). Мосты 2000 . Конференция по мостам. стр. 239–246.

[1]

[2]

[3]