Псевдооднородный многогранник
Псевдооднородный , многогранник — это многогранник , который имеет правильные многоугольники в качестве граней и имеет одинаковую конфигурацию вершин во всех вершинах но не является вершинно-транзитивным : неверно, что для любых двух вершин существует симметрия многогранника, отображающая первую изометрически на второй. Таким образом, хотя все вершины псевдооднородного многогранника кажутся одинаковыми, он не является изогональным . Их называют псевдооднородными многогранниками из-за их сходства с некоторыми истинными однородными многогранниками .
Известны два псевдооднородных многогранника: псевдоромбокубооктаэдр и псевдобольшой ромбокубооктаэдр . Неизвестно, есть ли еще какие-нибудь; Бранко Грюнбаум предположил, что это не так, но подумал, что доказательство будет «вероятно, довольно сложным». [1] Они оба имеют симметрию D 4d , ту же симметрию, что и квадратная антипризма . Оба их можно построить из однородного многогранника , скрутив одну куполообразную шапку.
Псевдооднородные многогранники
[ редактировать ]Псевдоромбокубооктаэдр
[ редактировать ]Псевдоморомбикубооктаэдр — единственный выпуклый псевдооднородный многогранник. Это также тело Джонсона (J 37 ) и его также можно назвать вытянутым квадратным гиробикуполом . Его двойником является псевдодельтоидный икоситетраэдр . Как следует из названия, его можно построить, удлинив квадратный гиробикупол ( J 29 ) и вставив восьмиугольную призму между двумя его половинками. Полученное тело является локально вершинно-регулярным - расположение четырех граней, инцидентных любой вершине, одинаково для всех вершин; это уникальное явление среди твердых тел Джонсона. Однако оно не является вершинно-транзитивным и, следовательно, не является одним из архимедовых тел , поскольку существуют пары вершин, в которых нет изометрии тела, отображающей одно в другое. По сути, два типа вершин можно отличить по их «соседям соседей». Другой способ убедиться в том, что многогранник не является правильным по вершинам, - это заметить, что вокруг его экватора имеется ровно один пояс из восьми квадратов, что отличает вершины на поясе от вершин с обеих сторон.
 Ромбокубооктаэдр |  Разобранные секции |  Псевдоромбокубооктаэдр |
Твердое тело также можно рассматривать как результат скручивания одного из квадратных куполов ( J 4 ) на ромбокубооктаэдре (одном из архимедовых тел ; он же вытянутый квадратный ортобикупол) на 45 градусов. Его сходство с ромбокубооктаэдром дает ему альтернативное название псевдоромбокубооктаэдр . Его иногда называют «четырнадцатым архимедовым телом».
Если лица окрашены в соответствии с симметрией D 4d , это может выглядеть так:
| псевдоромбокубооктаэдр | Псевдодельтоидный икоситетраэдр Двойной многогранник | |
|---|---|---|
 сеть |  |  |
расположены 8 (зеленых) квадратов Вокруг экватора , 4 (красных) треугольника и 4 (желтых) квадрата сверху и снизу, а также по одному (синему) квадрату на каждом полюсе.
Построение однородных и псевдоромбокубооктаэдров можно увидеть в следующих увеличениях восьмиугольной призмы:
 Восьмиугольная призма (окрашена с симметрией D 8h )... | 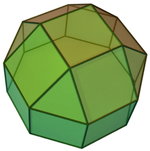 ...с одним из восьмиугольников, дополненным квадратным куполом. |  Есть два варианта ориентации другого непересекающегося квадратного купола. Совмещают соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и получают ромбокубооктаэдр. Эта конструкция имеет симметрию D 4h , хотя ромбокубооктаэдр обладает полной октаэдрической симметрией. | 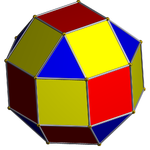 Другой вариант выравнивает несоответствующие грани (треугольники с квадратами) и создает псевдоромбокубооктаэдр . Эта конструкция имеет симметрию D 4d . |
Псевдобольшой ромбокубооктаэдр
[ редактировать ]Однородный невыпуклый большой ромбокубооктаэдр можно рассматривать как октаграммную призму с выемками октаграмм со скрещенными квадратными куполами, аналогично тому, как ромбокубооктаэдр можно рассматривать как восьмиугольную призму с восьмиугольниками, дополненными квадратными куполами. Вращение одного из куполов в этой конструкции приводит к образованию псевдобольшого ромбокубооктаэдра .
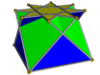 Перекрещенный квадратный купол |  Невыпуклый большой ромбокубооктаэдр |  Псевдобольшой ромбокубооктаэдр |
На фотографиях ниже показаны раскопки октаграммной призмы со скрещенными квадратными куполами, происходящие поэтапно. Пересеченные квадратные купола всегда красного цвета, а квадратные стороны октаграммной призмы — других цветов. Все изображения ориентированы примерно одинаково для наглядности.
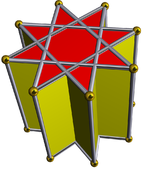 Октаграммная призма (окрашена в цвет симметрии D 8h )... | 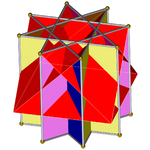 ...с одной из октаграмм (здесь, верхней) с выкопанным скрещенным квадратным куполом. Это можно назвать удлиненным скрещенным квадратным куполом или увеличенной октаграммной призмой Джонсона , и оно изоморфно удлиненному квадратному куполу . | 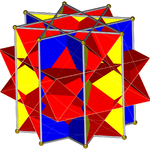 Есть два варианта ориентации другого скрещенного квадратного купола. Сопоставляем соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и получаем невыпуклый большой ромбокубооктаэдр. Эта конструкция имеет симметрию D 4h , хотя невыпуклый большой ромбокубооктаэдр обладает полной октаэдрической симметрией . | 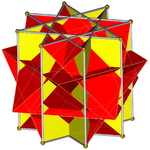 Другой вариант выравнивает несоответствующие грани (треугольники с квадратами) и создает псевдобольшой ромбокубооктаэдр (или псевдоквазиромбокубооктаэдр). Эта конструкция имеет симметрию D 4d . |
Псевдобольшой ромбокубооктаэдр имеет единственный «пояс» квадратов вокруг экватора и может быть построен путем скручивания одного из скрещенных квадратных куполов невыпуклого большого ромбокубооктаэдра на 45 градусов. Это аналог псевдоромбокубооктаэдра.
Двойники псевдооднородных многогранников
[ редактировать ]псевдооднородных У двойственных многогранников все грани конгруэнтны , но не транзитивны: не все их грани лежат на одной и той же орбите симметрии , и поэтому они не изоэдральны . Это следствие того, что псевдооднородные многогранники имеют одинаковую конфигурацию вершин в каждой вершине, но не являются вершинно-транзитивными . Об этом свидетельствуют разные цвета, использованные для граней на изображениях двойственных псевдооднородных многогранников в этой статье, обозначающие разные типы граней.
Псевдодельтоидный икоситетраэдр
[ редактировать ]Псевдобольшой дельтовидный икоситетраэдр
[ редактировать ]Ссылки
[ редактировать ]- ^ Грюнбаум, Бранко (2009), «Непреходящая ошибка» (PDF) , Elemente der Mathematik , 64 (3): 89–101, doi : 10.4171/EM/120 , MR 2520469 . Перепечатано в Питичи, Мирча, изд. (2011). Лучшее сочинение по математике 2010 года . Издательство Принстонского университета. стр. 18–31. .

