Перекрещенный квадратный купол
| Перекрещенный квадратный купол | |
|---|---|
 | |
| Тип | Джонсона изоморф Купол |
| Лица | 4 треугольника 1+4 квадрата 1 октаграмма |
| Края | 20 |
| Вершины | 12 |
| Конфигурация вершин | 4+4(3.4.8/3) 4(3/2.4 3 ) |
| Символ Шлефли | {4/3} || т{4/3} |
| Группа симметрии | С 4в , [4], (*44) |
| Группа вращения | С 4 , [4] + , (44) |
| Двойной многогранник | - |
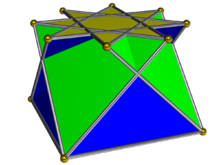
В геометрии скрещенный квадратный купол — один из изоморфов невыпуклого твердого тела Джонсона , топологически идентичный выпуклому квадратному куполу . Его можно получить как срез невыпуклого большого ромбокубооктаэдра или квазиромбокубооктаэдра. Как и во всех куполах , базовый многоугольник имеет в два раза больше ребер и вершин , чем верхний; в данном случае базовым многоугольником является октаграмма .
Его можно рассматривать как купол с ретроградным квадратным основанием, так что квадраты и треугольники соединяются через основания противоположно квадратному куполу, следовательно, пересекая друг друга.
Связанные многогранники
[ редактировать ]| 4 | 5 | 7 | 8 | n ⁄ d |
|---|---|---|---|---|
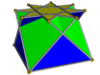 {4/3} Перекрещенный квадратный купол (с ног на голову) |  {5/3} Перекрещенный пентаграммный купол (с ног на голову) |  {7/3} Гептаграммный купол |  {8/3} Октаграммный купол | 3 |
| — | — |  {7/5} Скрещенный гептаграммный купол (с ног на голову) |  {8/5} Скрещенный октаграммный купол | 5 |
Перекрещенный квадратный купол можно рассматривать как часть некоего однородного многогранника. Например, большой кубооктаэдр можно рассматривать как шесть скрещенных квадратных куполов, соединенных своими треугольными гранями, а невыпуклый большой ромбокубооктаэдр можно рассматривать как смесь шести куполов. Кроме того, невыпуклый большой ромбокубооктаэдр можно рассматривать как октаграммную призму с выемками октаграмм со скрещенными квадратными куполами, аналогично тому, как ромбокубооктаэдр можно рассматривать как восьмиугольную призму с восьмиугольниками, дополненными квадратными куполами. Вращение одного из куполов в этой конструкции приводит к образованию псевдобольшого ромбокубооктаэдра . К этому можно добавить большой ромбогексаэдр как единственную из всех трех октаграммных призм, которые можно использовать для построения невыпуклого большого ромбокубооктаэдра.
 Перекрещенный квадратный купол |  Невыпуклый большой ромбокубооктаэдр |  Псевдобольшой ромбокубооктаэдр |  Большой кубический октаэдр |  Большой ромбогексаэдр |
На фотографиях ниже показаны раскопки октаграммной призмы со скрещенными квадратными куполами, происходящие поэтапно. Пересеченные квадратные купола всегда красного цвета, а квадратные стороны октаграммной призмы — других цветов. Все изображения ориентированы примерно одинаково для наглядности.
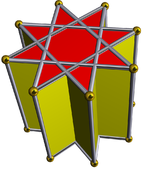 Октаграммная призма (окрашена в цвет симметрии D 8h )... | 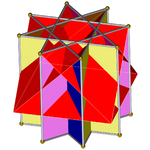 ...с одной из октаграмм (здесь, верхней) с выкопанным скрещенным квадратным куполом. Это можно назвать ретро-удлиненным скрещенным квадратным куполом или увеличенной октаграммной призмой , и оно изоморфно удлиненному квадратному куполу Джонсона . | 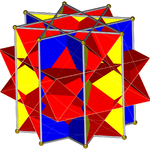 Есть два варианта ориентации другого скрещенного квадратного купола. Сопоставляем соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и получаем невыпуклый большой ромбокубооктаэдр. Эта конструкция имеет симметрию D 4h , хотя невыпуклый большой ромбокубооктаэдр обладает полной октаэдрической симметрией . | 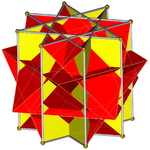 Другой вариант выравнивает несоответствующие грани (треугольники с квадратами) и создает псевдобольшой ромбокубооктаэдр (или псевдоквазиромбокубооктаэдр). Эта конструкция имеет симметрию D 4d . |
Эту серию раскопок можно легко сравнить с соответствующей серией увеличений восьмиугольной призмы:
 Восьмиугольная призма (окрашена с симметрией D 8h )... | 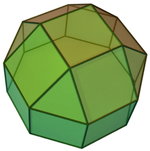 ...с одним из восьмиугольников, дополненным квадратным куполом. |  Есть два варианта ориентации другого скрещенного квадратного купола. Совмещают соответствующие грани (треугольники с треугольниками, квадраты с квадратами) и получают ромбокубооктаэдр. Эта конструкция имеет симметрию D 4h , хотя ромбокубооктаэдр обладает полной октаэдрической симметрией. | 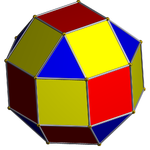 Другой вариант выравнивает несоответствующие грани (треугольники с квадратами) и создает псевдоромбокубооктаэдр . Эта конструкция имеет симметрию D 4d . |
Двойной многогранник
[ редактировать ]Двойной скрещенный квадратный купол имеет 8 треугольных и 4 коршунных грани:
Из-за того, что грани скрещенного квадратного купола проходят близко к его центру, этот двойник очень остроконечным выглядит . Это также происходит для двойственных однородных многогранников, известных как большой пентакисдодекаэдр (DU 58 ) и средний перевернутый пятиугольный гексеконтаэдр (DU 60 ).
Ссылки
[ редактировать ]- Джим Макнил, Купол ИЛИ Полукупол
- Джим Макнил, Связь куполов с однородными многогранниками
