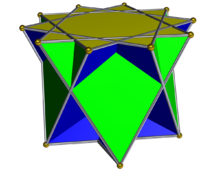
Перекрещенный пентаграммный купол
| Перекрещенный пентаграммный купол | |
|---|---|
 | |
| Тип | Джонсона изоморф Купол |
| Лица | 5 треугольников 5 квадратов 1 пентаграмма 1 декаграмм |
| Края | 25 |
| Вершины | 15 |
| Конфигурация вершин | 5+5(3.4.10/3) 5(3.4.5/3.4) |
| Символ Шлефли | {5/3} || т{5/3} |
| Группа симметрии | С 5в , [5], (*55) |
| Группа вращения | С 5 , [5] + , (55) |
| Двойной многогранник | - |
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( июнь 2021 г. ) |
В геометрии скрещенный пентаграммный купол — одна из невыпуклых изоморф твердого тела Джонсона , топологически идентичный выпуклому пятиугольному куполу . Его можно получить как срез большого ромбокосододекаэдра или квазимробикосидодекаэдра. Как и во всех куполах , базовый многоугольник имеет в два раза больше ребер и вершин , чем верхний; в этом случае базовым многоугольником является декаграмма .
Его можно рассматривать как купол с ретроградным пентаграммным основанием, так что квадраты и треугольники соединяются через основания противоположным пентаграммному куплоиду способом , следовательно, более глубоко пересекая друг друга.
Связанные многогранники
[ редактировать ]| 4 | 5 | 7 | 8 | n ⁄ d |
|---|---|---|---|---|
 {4/3} Перекрещенный квадратный купол (с ног на голову) |  {5/3} Перекрещенный пентаграммный купол (с ног на голову) |  {7/3} Гептаграммный купол |  {8/3} Октаграммный купол | 3 |
| — | — |  {7/5} Скрещенный гептаграммный купол (с ног на голову) |  {8/5} Скрещенный октаграммный купол | 5 |
Скрещенный пятиугольный купол можно рассматривать как часть однородных многогранников, известных как невыпуклый большой ромбикосододекаэдр , большой додецикосододекаэдр и большой ромбидодекаэдр .
 Перекрещенный пентаграммный купол |  Невыпуклый большой ромбокосододекаэдр |  Большой додецикосододекаэдр |  Большой ромбидодекаэдр |
Различные скрещенные пентаграммные купола на невыпуклом большом ромбикосидодекаэдре можно уменьшить или вращать (вращать), чтобы получить набор из 12 многогранников, изоморфных телам Джонсона от J 72 до J 83 . Это вращающиеся, метабигратные, парабигратные, тригиратные, уменьшенные, метабидиминированные, парабидиминированные, тройные уменьшенные, уменьшенные метавращающиеся, уменьшенные парагиратные, уменьшенные бигиратные и вращающиеся двууменьшенные квазимробикосидодекаэдры.
Двойной многогранник
[ редактировать ]Двойной скрещенный пентаграммный купол имеет 10 треугольных и 5 коршунных граней:
Ссылки
[ редактировать ]- Джим Макнил, Связь куполов с однородными многогранниками
- Джим Макнил, Купол ИЛИ Полукупол
- Ричард Клитцинг, Осесимметричные грани однородных многогранников
