Пятиугольный купол
| Пятиугольный купол | |
|---|---|
 | |
| Тип | Джонсон В 4 – В 5 – В 6 |
| Лица | 5 треугольников 5 квадратов 1 пятиугольник 1 декагон |
| Края | 25 |
| Вершины | 15 |
| Конфигурация вершин | 10(3.4.10) 5(3.4.5.4) |
| Группа симметрии | С 5в , [5], (*55) |
| Группа ротации | С 5 , [5] + , (55) |
| Двойной многогранник | - |
| Характеристики | выпуклый |
| Сеть | |
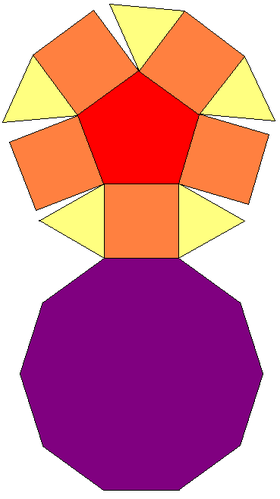 | |

В геометрии пятиугольный купол — одно из тел Джонсона ( J 5 ). Его можно получить как срез ромбокододекаэдра . Пятиугольный купол состоит из 5 равносторонних треугольников , 5 квадратов , 1 пятиугольника и 1 десятиугольника .
Тело Джонсона — это один из 92 строго выпуклых многогранников , которые состоят из правильных многоугольных граней, но не являются однородными многогранниками (то есть не являются платоновыми телами , архимедовыми телами , призмами или антипризмами ). Их назвал Норман Джонсон , который впервые перечислил эти многогранники в 1966 году. [1]
Формулы
[ редактировать ]Следующие формулы для объема , площади поверхности и радиуса описанной окружности можно использовать, если все , с грани правильные длиной ребра a : [2]
Высота составляет пятиугольного купола [3]
- .
Связанные многогранники
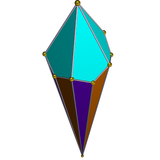
[ редактировать ]Двойной многогранник
[ редактировать ]Двойной пятиугольный купол имеет 10 треугольных граней и 5 кайт-граней:
| Двойной пятиугольный купол | Чистая двойная | 3D model |
|---|---|---|
 |  |  |
Другие выпуклые купола
[ редактировать ]| н | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Символ Шлефли | {2} || т{2} | {3} || т{3} | {4} || т{4} | {5} || т{5} | {6} || т{6} | {7} || т{7} | {8} || т{8} |
| Купол |  Диагональный купол |  Треугольный купол |  Квадратный купол |  Пятиугольный купол |  Шестиугольный купол (Плоский) |  Семиугольный купол (Необычное лицо) |  Восьмиугольный купол (Необычное лицо) |
| Связанный униформа многогранники | Ромбоэдр | Кубооктаэдр | Ромбокубооктаэдр | Ромбикосидодекаэдр | Ромбитригексагональная мозаика | Ромбитригептагональная черепица | Ромбитриоктагональная черепица |
Перекрещенный пентаграммный купол
[ редактировать ]
В геометрии скрещенный пентаграммный купол является одной из невыпуклых изоморф твердого тела Джонсона , топологически идентичен выпуклому пятиугольному куполу. Его можно получить как срез большого невыпуклого ромбикосододекаэдра или квазиромбикосододекаэдра, аналогично тому, как пятиугольный купол можно получить как срез ромбикосидодекаэдра. Как и во всех куполах, базовый многоугольник имеет в два раза больше ребер и вершин , чем верхний; в этом случае базовым многоугольником является декаграмма .
Его можно рассматривать как купол с ретроградным пентаграммным основанием, так что квадраты и треугольники соединяются через основания противоположным пентаграммному куплоиду способом , следовательно, более глубоко пересекая друг друга.
Ссылки
[ редактировать ]- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , Zbl 0132.14603 .
- ^ Стивен Вольфрам , « Пятиугольный купол » от Wolfram Alpha . Проверено 11 апреля 2020 г.
- ^ Сапинья, Р. «Площадь и объем тела Джонсона J 5 » . Проблемы и экуасионы (на испанском языке). ISSN 2659-9899 . Проверено 16 июля 2020 г.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. , « Пятиугольный купол » (« Тело Джонсона ») в MathWorld .



