дисфеноцинальный

дисфеноцинальный
Тип	Джонсон Я 89 – Я 90 – Я 91
Лица	20 треугольников 4 квадрата
Края	38
Вершины	16
Конфигурация вершин	4(3 2 .4 2 ) 4(3 5 ) 8(3 4 .4)
Группа симметрии	Д 2д
Характеристики	выпуклый
Сеть

3D-модель дисфеноцингулума

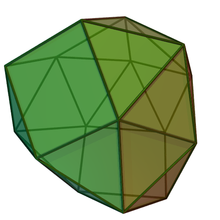
В геометрии дисфеноцингулум представляет собой тело Джонсона с 20 равносторонними треугольниками и 4 квадратами в качестве граней.

Характеристики

Дисфеноцингулум назван Джонсоном (1966) . Приставка дисфено- относится к двум клиновидным комплексам, каждый из которых образован двумя соседними лунками — фигурой из двух равносторонних треугольников на противоположных сторонах квадрата . Суффикс -cingulum , буквально «пояс», относится к полосе из 12 треугольников, соединяющих два клина. Получившийся многогранник имеет 20 равносторонних треугольников и 4 квадрата, образующих 24 грани. . Все грани правильные , что позволяет отнести дисфеноцингулум к телу Джонсона — выпуклому многограннику, в котором все его грани представляют собой правильный многоугольник, — указанному как 90-е тело Джонсона. $J_{90}$. . Он элементарный, то есть его нельзя разделить плоскостью на два небольших правильных многогранника.

Площадь поверхности дисфеноцингулума с длиной края $a$ можно определить, сложив все его грани, площади 20 равносторонних треугольников и 4 квадратов. $(4+5{\sqrt {3}})a^{2}\approx 12.6603a^{2}$, а его объем $3.7776a^{3}$.

Декартовы координаты

Позволять $a\approx 0.76713$ быть вторым наименьшим положительным корнем многочлена $${\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}\\&\quad {}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}$$и $h={\sqrt {2+8a-8a^{2}}}$ и $c={\sqrt {1-a^{2}}}$. Тогда декартовы координаты дисфеноцингулума с длиной ребра 2 задаются объединением орбит точек $$\left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)$$под действием группы , порожденной отражениями о плоскости xz и плоскости yz.

Внешние ссылки

• Вайсштейн, Эрик В. , « Дисфеноцингулум » (« Твердое тело Джонсона ») в MathWorld .