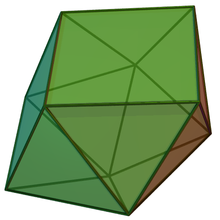
Сфенокорона

Сфенокорона
Сфенокорона
Тип	Джонсон ; Я 85 – Я 86 – Я 87
Лица	12 треугольников ; 2 квадрата
Края	22
Вершины	10
Конфигурация вершин	4(3 3 .4) ; 2(3 2 .4 2 ) ; 2x2(3 5 )
Группа симметрии	С 2 в
Двойной многогранник	-
Характеристики	выпуклый
Сеть

В геометрии сфенокорона представляет собой тело Джонсона с 12 равносторонними треугольниками и 2 квадратами в качестве граней.

Характеристики

Сфенокорона была названа Джонсоном (1966) , в котором он использовал приставку сфено-, обозначающую клиновидный комплекс, образованный двумя соседними лунками — квадрат с равносторонними треугольниками, прикрепленными на его противоположных сторонах. Суффикс -корона относится к коронообразному комплексу из 8 равносторонних треугольников. ^[1] В результате соединения обоих комплексов между собой полученный многогранник имеет 12 равносторонних треугольников и 2 квадрата , образующих 14 граней. ^[2] многогранник Выпуклый , у которого все грани являются правильными многоугольниками, называется телом Джонсона . Среди них - сфенокорона, обозначенная как 86-е твердое тело Джонсона. $J_{86}$ . ^[3] Он элементарен, то есть его нельзя разделить плоскостью на два небольших правильных многогранника. ^[4]

Площадь поверхности сфенокороны с длиной ребра $a$ можно рассчитать как: ^[2] $A=\left(2+3{\sqrt {3}}\right)a^{2}\approx 7.19615a^{2},$ и его объем как: ^[2] $\left({\frac {1}{2}}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}\right)a^{3}\approx 1.51535a^{3}.$

Декартовы координаты

Позволять $k\approx 0.85273$ быть наименьшим положительным корнем многочлена четвертой степени $60x^{4}-48x^{3}-100x^{2}+56x+23$ . Тогда декартовы координаты сфенокороны с длиной ребра 2 задаются объединением орбит точек $\left(0,1,2{\sqrt {1-k^{2}}}\right),\,(2k,1,0),\left(0,1+{\frac {\sqrt {3-4k^{2}}}{\sqrt {1-k^{2}}}},{\frac {1-2k^{2}}{\sqrt {1-k^{2}}}}\right),\,\left(1,0,-{\sqrt {2+4k-4k^{2}}}\right)$ под действием группы , порожденной отражениями о плоскости xz и плоскости yz. ^[5]

Вариации

Сфенокорона также является вершиной изогонального где n-угольного двойного антипризмоида, n — нечетное число, большее единицы, включая большую антипризму с парами трапеций, а не квадратных граней.

См. также

Дополненная сфенокорона

Ссылки

^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603
^ Jump up to: Перейти обратно: ^а ^б ^с Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245
^ Фрэнсис, Дэррил (2013), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177
^ Кромвель, PR (1997), Многогранники , Издательство Кембриджского университета , стр. 86–87, 89, ISBN 978-0-521-66405-9
^ Тимофеенко А.В. (2009), «Неплатоновые и неархимедовы некомпозитные многогранники», Journal of Mathematical Science , 162 (5): 718, doi : 10.1007/s10958-009-9655-0 , S2CID 120114341

Внешние ссылки

Вайсштейн, Эрик В. , « Sphenocorona » (« Тело Джонсона ») в MathWorld .

[johnson-1] Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603

[berman-2] Jump up to: Перейти обратно: ^а ^б ^с Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245

[francis-3] Фрэнсис, Дэррил (2013), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177

[cromwell-4] Кромвель, PR (1997), Многогранники , Издательство Кембриджского университета , стр. 86–87, 89, ISBN 978-0-521-66405-9

[timofeenko-5] Тимофеенко А.В. (2009), «Неплатоновые и неархимедовы некомпозитные многогранники», Journal of Mathematical Science , 162 (5): 718, doi : 10.1007/s10958-009-9655-0 , S2CID 120114341

[1]

[2]

[3]

[4]

[5]

v т и Твердые вещества Джонсона
Пирамиды , купола и круги	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Модифицированные пирамиды	вытянутая треугольная пирамида вытянутая квадратная пирамида вытянутая пятиугольная пирамида Гироудлиненная квадратная пирамида гироудлиненная пятиугольная пирамида треугольная бипирамида пятиугольная бипирамида вытянутая треугольная бипирамида вытянутая квадратная бипирамида вытянутая пятиугольная бипирамида гироудлиненная квадратная бипирамида
Модифицированные купола и раунды	удлиненный треугольный купол вытянутый квадратный купол удлиненный пятиугольный купол вытянутая пятиугольная ротонда гироудлинённый треугольный купол гироудлиненный квадратный купол гироудлиненный пятиугольный купол гироудлиненная пятиугольная ротонда гиробифастигий треугольный ортобикупол квадратный ортобикупол квадратный гиробикупол пятиугольный ортобикупол пятиугольный гирокупол пятиугольная ортокуполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда удлиненный треугольный ортобикупол удлиненный треугольный гиробикупол вытянутый квадратный гиробикупол удлиненный пятиугольный ортобикупол удлиненный пятиугольный гиробикупол вытянутая пятиугольная ортокуполаротонда вытянутая пятиугольная гирокуполаротонда вытянутая пятиугольная ортобиротонда вытянутая пятиугольная гиробиротунда гироудлиненный треугольный двуглавый купол гироудлиненный квадратный двуглавый купол гироудлиненный пятиугольный двуглавый купол гироудлинённый пятиугольный купол-ротонда гироудлиненная пятиугольная биротонда
Дополненные призмы	увеличенная треугольная призма смещенная треугольная призма триаугментированная треугольная призма увеличенная пятиугольная призма увеличенная пятиугольная призма дополненная шестиугольная призма парабиоувеличенная шестиугольная призма метаувеличенная шестиугольная призма трехугольная шестиугольная призма
Модифицированные платоновые тела	дополненный додекаэдр парабиоувеличенный додекаэдр метаувеличенный додекаэдр триаугментированный додекаэдр метабидиминированный икосаэдр трехмерный икосаэдр увеличенный трехмерный икосаэдр
Модифицированные архимедовы тела	расширенный усеченный тетраэдр дополненный усеченный куб увеличенный усеченный куб расширенный усеченный додекаэдр парабиоувеличенный усеченный додекаэдр метаувеличенный усеченный додекаэдр триаугментированный усеченный додекаэдр вращающийся ромбокосододекаэдр парабигиратный ромбикосидодекаэдр метабивративный ромбокосододекаэдр тригиратный ромбикосидодекаэдр уменьшенный ромбокосододекаэдр парагиратный уменьшенный ромбикосидодекаэдр метавращающийся уменьшенный ромбокосододекаэдр большой, уменьшенный ромбокосододекаэдр парабидиуменьшенный ромбокосододекаэдр метабидиминированный ромбикосододекаэдр вращающийся двууменьшенный ромбокосододекаэдр трехмерный ромбикосидодекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона расширенная сфенокорона сфеномегакорона Гебесфеномегакорона дисфенозин коды неисправностей треугольная гебесфеноротонда
(См. также Список твердых тел Джонсона , сортируемую таблицу)