Пятиугольная пирамида

Пятиугольная пирамида
Тип	Пирамида Джонсон Я 1 – Я 2 – Я 3
Лица	5 треугольников 1 пятиугольник
Края	10
Вершины	6
Конфигурация вершин	$5\times (3^{2}\times 5)+1\times 3^{5}$
Группа симметрии	$C_{5\mathrm {v} }$
Двугранный угол ( градусы )	В Джонсоне солидно: треугольник к треугольнику: 138,19° треугольник-пятиугольник: 37,37°
Двойной многогранник	самодвойственный
Характеристики	выпуклый , элементарный
Сеть

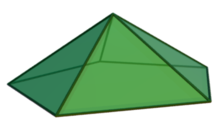
В геометрии пятиугольная пирамида — это пирамида с пятиугольным основанием и пятью треугольными гранями, всего шесть граней. Оно классифицируется как тело Джонсона, если все ребра равны по длине, образуя равносторонние треугольные грани и правильное пятиугольное основание. Пятиугольную пирамиду можно встретить во многих многогранниках, в том числе и в их конструкциях. Это также происходит в стереохимии в пятиугольной пирамидальной молекулярной геометрии .

Характеристики

Пятиугольная пирамида имеет шесть вершин, десять ребер и шесть граней. Одна из его граней — пятиугольник , основание пирамиды; пять других — треугольники . Пять ребер образуют пятиугольник, соединяя его пять вершин, а остальные пять ребер известны как боковые ребра пирамиды и встречаются в шестой вершине, называемой вершиной . Пятиугольная пирамида называется правильной, если ее основание описано в круге, образующем правильный пятиугольник , и правильной, если ее высота расположена перпендикулярно центру основания.

Как и другие правильные пирамиды с правильным многоугольником в основании, эта пирамида имеет пирамидальную симметрию циклической группы. $C_{5\mathrm {v} }$: пирамида остается неизменной при поворотах на один, два, три и четыре за пять полных оборотов вокруг своей оси симметрии , линии, соединяющей вершину с центром основания. Он также зеркально симметричен относительно любой перпендикулярной плоскости, проходящей через биссектрису основания. Его можно представить в виде кругового графа. $W_{5}$; в более общем смысле, круговой график $W_{n}$ изображение скелета представляет собой $n$- двусторонняя пирамида. Он самодуален , то есть его двойственный многогранник является самой пятиугольной пирамидой.

3D модель пятиугольной пирамиды.

Когда все ребра равны по длине, пять треугольных граней равносторонние , а основание представляет собой правильный пятиугольник. Эта пирамида обладает свойством твердого тела Джонсона. $J_{2}$, выпуклый многогранник, у которого все грани являются правильными многоугольниками . Двугранный угол между двумя соседними треугольными гранями составляет примерно 138,19 °, а между треугольной гранью и основанием - 37,37 °. Это элементарные многогранники , то есть их нельзя разделить плоскостью для создания двух маленьких выпуклых многогранников с правильными гранями. При условии $a$ длина всех ребер пятиугольной пирамиды. сумме Площадь поверхности многогранника равна площадей его граней. Следовательно, площадь поверхности пятиугольной пирамиды равна сумме четырех треугольников и площади одного пятиугольника. Объем каждой пирамиды равен одной трети площади ее основания, умноженной на ее высоту. То есть объем пятиугольной пирамиды составляет одну треть произведения высоты и площади пятиугольной пирамиды. В случае тела Джонсона с длиной ребра $a$, его площадь поверхности $A$ и объем $V$ являются: $${\begin{aligned}A&={\frac {a^{2}}{2}}{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\approx 3.88554a^{2},\\V&={\frac {5+{\sqrt {5}}}{24}}a^{3}\approx 0.30150a^{3}.\end{aligned}}$$

Приложения

В многограннике

Пятиугольные пирамиды можно найти в небольшом звездчатом додекаэдре.

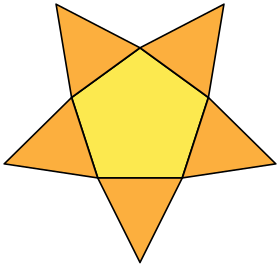
Пятиугольные пирамиды можно встретить как компоненты многих многогранников. Прикрепление его основания к пятиугольной грани другого многогранника является примером процесса построения, известного как увеличение , а прикрепление его к призмам или антипризмам известно как удлинение или гироудлинение соответственно. Примерами многогранников являются пентакисдодекаэдр , построенный из додекаэдра путем прикрепления оснований пятиугольных пирамид к каждой пятиугольной грани, малый звездчатый додекаэдр, построенный из правильного додекаэдра, звездчатого пятиугольных пирамид, и правильный икосаэдр, построенный из пятиугольной антипризмы путем соединения двух пятиугольных пирамид. на его пятиугольные основания.

Некоторые тела Джонсона построены либо путем увеличения пятиугольных пирамид, либо путем дополнения других форм пятиугольными пирамидами: удлиненная пятиугольная пирамида. $J_{9}$, гировытянутая пятиугольная пирамида $J_{11}$, пятиугольная бипирамида $J_{13}$, вытянутая пятиугольная бипирамида $J_{16}$, дополненный додекаэдр $J_{58}$, парабиаувеличенный додекаэдр $J_{59}$, метаувеличенный додекаэдр $J_{60}$и триаугментированный додекаэдр $J_{61}$. Соответственно, удаление пятиугольной пирамиды из многогранников является примером, известным как уменьшение ; метабидиминированный икосаэдр $J_{62}$ и трехмерный икосаэдр $J_{63}$ приведены примеры, в которых их конструкции начинаются с удаления пятиугольных пирамид из правильного икосаэдра .

Стереохимия

В стереохимии кластер атомов может иметь пятиугольную пирамидальную геометрию . Эта молекула имеет элемент основной группы с одной активной неподеленной парой, которую можно описать моделью, предсказывающей геометрию молекул, известной как теория VSEPR . Примером молекулы с такой структурой может служить нидо -клеточный карбонат CB ₅ H ₉ .

Ссылки

• Болл, WWR; Коксетер, HSM (1987). Математические развлечения и очерки . Дуврские публикации. ISBN  978-0-486-25357-2 .
• Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР   0290245 .
• Калтер, Пол А.; Колтер, Майкл А. (2011). Техническая математика . Джон Уайли и сыновья . ISBN  978-0-470-53492-2 .
• Чолак, Зейнеп; Гельсген, Озджан (2015). «Новые метрики для дельтоидного гексаконтаэдра и пентакис додекаэдра». Научный журнал Университета Сакарья . 19 (3): 353–360. дои : 10.16984/saufenbilder.03497 .
• Гргич, Иван; Каракашич, Мирко; Ивандич, Желько; Главаш, Хрвое (2022). «Сохранение знаний о проектировании начертательной геометрии». В Главаше, Хрвое; Хадзима-Ньярко, Марияна; Каракашич, Мирко; Адемович, Найда; Авдакович, Самир (ред.). 30-я Международная конференция по организации и технологии технического обслуживания (ОТО 2021): Материалы 30-й Международной конференции по организации и технологии технического обслуживания (ОТО 2021) . Международная конференция по организации и технологии технического обслуживания. дои : 10.1007/978-3-030-92851-3 .
• Хартшорн, Робин (2000). Геометрия: Евклид и не только . Тексты для бакалавриата по математике. Спрингер-Верлаг. ISBN  9780387986500 .
• Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР   0185507 . S2CID   122006114 . Збл   0132.14603 .
• Каппрафф, Джей (2001). Связи: Геометрический мост между искусством и наукой (2-е изд.). Всемирная научная . ISBN  981-02-4585-8 .
• Макартни, Д.Х. (2017). «Кукурбитурилы в связывании и доставке лекарств». В Гокеле, Джордже В.; Барбур, Леонард Дж. (ред.). Комплексная супрамолекулярная химия II . Эльзевир. ISBN  978-0-12-803198-8 .
• Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри (2002). Общая химия: принципы и современные приложения . Том. 1. Прентис Холл . ISBN  9780130143297 .
• Писанский, Томаж; Серватиус, Бриджит (2013). Конфигурация с графической точки зрения . Спрингер. дои : 10.1007/978-0-8176-8364-1 . ISBN  978-0-8176-8363-4 .
• Поля, Г. (1954). Математика и правдоподобные рассуждения: индукция и аналогия в математике . Издательство Принстонского университета. ISBN  0-691-02509-6 .
• Раджваде, Арканзас (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта . Тексты и чтения по математике. Книжное агентство Индостан. дои : 10.1007/978-93-86279-06-4 . ISBN  978-93-86279-06-4 .
• Сильвестр, Джон Р. (2001). Геометрия: древняя и современная . Издательство Оксфордского университета.
• Слободан, Мишич; Обрадович, Мария; Джуканович, Гордана (2015). «Композитные вогнутые купола как геометрические и архитектурные формы» (PDF) . Журнал геометрии и графики . 19 (1): 79–91.
• Смит, Джеймс Т. (2000). Методы геометрии . Джон Уайли и сыновья . ISBN  0-471-25183-6 .
• Уэхара, Рюхэй (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии . Спрингер. дои : 10.1007/978-981-15-4470-5 . ISBN  978-981-15-4470-5 .
• Воллебен, Ева (2019). «Двойственность в неполиэдрических телах. Часть I: Полилайнер». В Коккьярелле, Луиджи (ред.). ICGG 2018 — Материалы 18-й Международной конференции по геометрии и графике: 40-летие — Милан, Италия, 3-7 августа 2018 г. Международная конференция по геометрии и графике. Спрингер. дои : 10.1007/978-3-319-95588-9 . ISBN  978-3-319-95588-9 .

Внешние ссылки

• Вайсштейн, Эрик В. , « Пятиугольная пирамида » (« Тело Джонсона ») в MathWorld .
• Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников ( VRML модель )