Вытянутый треугольный купол

Вытянутый треугольный купол
Вытянутый треугольный купол
Тип	Джонсон ; Я 17 – Я 18 – Я 19
Лица	4 треугольника ; 9 квадратов ; 1 шестиугольник
Края	27
Вершины	15
Конфигурация вершин	6(4 2 .6) ; 3(3.4.3.4) ; 6(3.4 3 )
Группа симметрии	С 3В
Двойной многогранник	-
Характеристики	выпуклый
Сеть

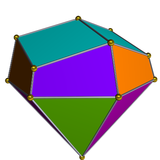
В геометрии вытянутый треугольный купол представляет собой многогранник, построенный из шестиугольной призмы путем присоединения треугольного купола . Это пример твердого тела Джонсона .

Строительство

Удлиненный треугольный купол построен из шестиугольной призмы путем прикрепления треугольного купола к одному из ее оснований - процесс, известный как удлинение . ^[1] Этот купол закрывает шестиугольную грань так, что образующийся многогранник имеет четыре равносторонних треугольника , девять квадратов и один правильный шестиугольник . ^[2] многогранник Выпуклый , все грани которого являются правильными многоугольниками, называется телом Джонсона . Вытянутый треугольный купол — один из них, названный восемнадцатым корпусом Джонсона. $J_{18}$ . ^[3]

Характеристики

Площадь поверхности вытянутого треугольного купола $A$ представляет собой сумму площадей всех многоугольных граней. Объем вытянутого треугольного купола можно определить, расчленив его на купол и шестиугольную призму, после чего суммируя их объемы. Учитывая длину ребра $a$ , его поверхность и объем можно сформулировать как: ^[2] ${\begin{aligned}A&={\frac {18+5{\sqrt {3}}}{2}}a^{2}&\approx 13.330a^{2},\\V&={\frac {5{\sqrt {2}}+9{\sqrt {3}}}{6}}a^{3}&\approx 3.777a^{3}.\end{aligned}}$

Он имеет ту же трехмерную симметрию, что и треугольный купол, циклическая группа. $C_{3\mathrm {v} }$ порядка 6. Его двугранный угол можно вычислить сложением угла треугольного купола и шестиугольной призмы: ^[4]

двугранный угол вытянутого треугольного купола между квадратом и треугольником равен углу треугольного купола между ними: 125,3°;
двугранный угол вытянутого треугольного купола между двумя соседними квадратами — угол шестиугольной призмы, внутренний угол ее основания 120°;
двугранный угол шестиугольной призмы между квадратом и шестиугольником составляет 90 °, угол треугольного купола между квадратом и шестиугольником составляет 54,7 °, а угол треугольного купола между треугольником и шестиугольником составляет 70,5 °. Следовательно, удлиненный треугольный купол между квадратом и квадратом, на ребре, где треугольный купол прикреплен к шестиугольной призме, равен 90 ° + 54,7 ° = 144,7 ° и 90 ° + 70,5 ° = 166,5. ° соответственно.

Двойной многогранник

Двойной удлиненно-треугольный купол имеет 15 граней: 6 равнобедренных треугольников, 3 ромба и 6 четырехугольников.

Двойная вытянутая треугольная главка	Чистая двойная

Связанные многогранники и соты

Вытянутый треугольный купол может образовывать мозаику пространства тетраэдрами пирамидами и квадратными . ^[5]

Ссылки

^ Раджваде, А.Р. (2001), Выпуклые многогранники с условиями регулярности и третья проблема Гильберта , Тексты и материалы по математике, Книжное агентство Hindustan, стр. 84–89, номер домена : 10.1007/978-93-86279-06-4 , ISBN. 978-93-86279-06-4 .
^ Jump up to: Перейти обратно: ^а ^б Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .
^ Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .
^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .
^ «Соты J18» .

Внешние ссылки

Вайсштейн, Эрик В. , « Удлиненный треугольный купол » (« Твердое тело Джонсона ») в MathWorld .

[rajwade-1] Раджваде, А.Р. (2001), Выпуклые многогранники с условиями регулярности и третья проблема Гильберта , Тексты и материалы по математике, Книжное агентство Hindustan, стр. 84–89, номер домена : 10.1007/978-93-86279-06-4 , ISBN. 978-93-86279-06-4 .

[berman-2] Jump up to: Перейти обратно: ^а ^б Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352, doi : 10.1016/0016-0032(71)90071-8 , MR 0290245 .

[francis-3] Фрэнсис, Дэррил (август 2013 г.), «Твердые тела Джонсона и их сокращения» , Word Ways , 46 (3): 177 .

[johnson-4] Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Canadian Journal of Mathematics , 18 : 169–200, doi : 10.4153/cjm-1966-021-8 , MR 0185507 , S2CID 122006114 , Zbl 0132.14603 .

[5] «Соты J18» .

[1]

[2]

[3]

[4]

[5]

v т и Твердые вещества Джонсона
Пирамиды , купола и круги	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Модифицированные пирамиды	вытянутая треугольная пирамида вытянутая квадратная пирамида вытянутая пятиугольная пирамида Гироудлиненная квадратная пирамида гироудлиненная пятиугольная пирамида треугольная бипирамида пятиугольная бипирамида вытянутая треугольная бипирамида вытянутая квадратная бипирамида вытянутая пятиугольная бипирамида гироудлиненная квадратная бипирамида
Модифицированные купола и раунды	удлиненный треугольный купол вытянутый квадратный купол удлиненный пятиугольный купол вытянутая пятиугольная ротонда Гироудлиненный треугольный купол гироудлиненный квадратный купол гироудлиненный пятиугольный купол гироудлиненная пятиугольная ротонда гиробифастигий треугольный ортобикупол квадратный ортобикупол квадратный гиробикупол пятиугольный ортобикупол пятиугольный гирокупол пятиугольная ортокуполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда удлиненный треугольный ортобикупол удлиненный треугольный гиробикупол вытянутый квадратный гиробикупол удлиненный пятиугольный ортобикупол удлиненный пятиугольный гиробикупол вытянутая пятиугольная ортокуполаротонда вытянутая пятиугольная гирокуполаротонда вытянутая пятиугольная ортобиротонда вытянутая пятиугольная гиробиротунда гироудлиненный треугольный двуглавый купол гироудлиненный квадратный двуглавый купол гироудлиненный пятиугольный двуглавый купол гироудлиненный пятиугольный купол-ротонда гироудлиненная пятиугольная биротонда
Дополненные призмы	увеличенная треугольная призма смещенная треугольная призма триаугментированная треугольная призма увеличенная пятиугольная призма увеличенная пятиугольная призма дополненная шестиугольная призма парабиоувеличенная шестиугольная призма метаувеличенная шестиугольная призма трехугольная шестиугольная призма
Модифицированные платоновые тела	дополненный додекаэдр парабиоувеличенный додекаэдр метаувеличенный додекаэдр триаугментированный додекаэдр метабидиминированный икосаэдр трехмерный икосаэдр увеличенный трехмерный икосаэдр
Модифицированные архимедовы тела	расширенный усеченный тетраэдр дополненный усеченный куб увеличенный усеченный куб дополненный усеченный додекаэдр парабиоувеличенный усеченный додекаэдр метаувеличенный усеченный додекаэдр триаугментированный усеченный додекаэдр вращающийся ромбокосододекаэдр парабигиратный ромбикосидодекаэдр метабивративный ромбокосододекаэдр тригиратный ромбикосидодекаэдр уменьшенный ромбокосододекаэдр парагиратный уменьшенный ромбокосододекаэдр метавращающийся уменьшенный ромбокосододекаэдр большой, уменьшенный ромбокосододекаэдр парабидиуменьшенный ромбокосододекаэдр метабидиминированный ромбикосододекаэдр вращающийся двууменьшенный ромбокосододекаэдр трехмерный ромбикосидодекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона расширенная сфенокорона сфеномегакорона Гебесфеномегакорона дисфеномен коды неисправностей треугольная гебесфеноротонда
(См. также Список твердых тел Джонсона , сортируемую таблицу)