Вытянутая квадратная бипирамида

Вытянутая квадратная бипирамида
Вытянутая квадратная бипирамида
Тип	Джонсон ; Я 14 – Я 15 – Я 16
Лица	8 треугольников ; 4 квадрата
Края	20
Вершины	10
Конфигурация вершин
Группа симметрии
Двойной многогранник	квадратный раздвоенный
Характеристики	выпуклый
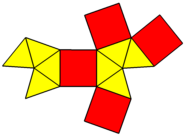
Сеть

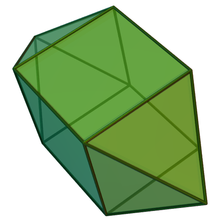
В геометрии вытянутая квадратная бипирамида (или вытянутый октаэдр ) — это многогранник, построенный путем прикрепления двух равносторонних квадратных пирамид к граням куба , противоположным друг другу. Его также можно рассматривать как 4 луны (квадраты с треугольниками на противоположных сторонах), соединенные между собой квадратами с квадратами и треугольниками с треугольниками. его также называют карандашным кубом или 12-гранным карандашным кубом . Из-за своей формы ^[1]^[2]

Кристалл циркона является примером вытянутой квадратной бипирамиды.

Строительство

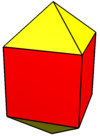
Вытянутая квадратная бипирамида строится путем присоединения двух равносторонних квадратных пирамид к граням куба , расположенным напротив друг друга. Этот процесс известен как удлинение . Эта конструкция включает удаление этих двух квадратов и замену их этими пирамидами, в результате чего восемь равносторонних треугольников и четыре квадрата. их гранями становятся ^[3]. Выпуклый многогранник, у которого все грани правильные, представляет собой тело Джонсона , а вытянутая квадратная бипирамида — одно из них, обозначаемое как $J_{15}$ , пятнадцатый твердый Джонсон. ^[4]

Характеристики

При условии $a$ — длина ребра вытянутой квадратной бипирамиды. Высоту вытянутой квадратной пирамиды можно вычислить, сложив высоты двух равносторонних квадратных пирамид и куба. Высота куба равна заданной длине ребра. $a$ , а высота равносторонней квадратной пирамиды равна $(1/{\sqrt {2}})a$ . Следовательно, высота вытянутой квадратной бипирамиды равна: ^[5] $a+2\cdot {\frac {1}{\sqrt {2}}}a=\left(1+{\sqrt {2}}\right)a\approx 2.414a.$ Площадь его поверхности можно вычислить, сложив все площади восьми равносторонних треугольников и четырех квадратов: ^[6] $\left(4+2{\sqrt {3}}\right)a^{2}\approx 7.464a^{2}.$ Его объем получается путем разрезания его на две равносторонние квадратные пирамиды и куб, а затем их сложения: ^[6] $\left(1+{\frac {\sqrt {2}}{3}}\right)a^{3}\approx 1.471a^{3}.$ Ее двугранный угол можно получить аналогично вытянутой квадратной пирамиде , сложив угол квадратных пирамид и куба: ^[7]

Двугранный угол вытянутой квадратной бипирамиды между двумя соседними треугольниками — это двугранный угол равностороннего треугольника между его боковыми гранями. $\arccos(-1/3)\approx 109.47^{\circ }$
Двугранный угол вытянутой квадратной бипирамиды между двумя соседними квадратами равен двугранному углу куба между ними. $\pi /2$
Двугранный угол равносторонней квадратной пирамиды между квадратом и треугольником равен $\arctan \left({\sqrt {2}}\right)\approx 54.74^{\circ }$ . Следовательно, двугранный угол вытянутой квадратной бипирамиды между треугольником и квадратом на ребре, где равносторонние квадратные пирамиды соединяют куб, равен $\arctan \left({\sqrt {2}}\right)+{\frac {\pi }{2}}\approx 144.74^{\circ }.$

Вытянутая квадратная бипирамида обладает двугранной симметрией , группой двугранников. $D_{4h}$ восьмого порядка: он имеет ось симметрии, проходящую через вершины квадратных пирамид и центр куба, и его внешний вид симметричен за счет отражения в горизонтальной плоскости. ^[7]

Связанные многогранники и соты

Вытянутая квадратная бипирамида двойственна квадрату бифрустума , имеющему восемь трапеций и два квадрата.

Особый вид вытянутой квадратной бипирамиды без правильных граней обеспечивает самотесселяцию евклидова пространства. Треугольники этой вытянутой квадратной бипирамиды неправильны ; они имеют ребра в соотношении 2: √ 3 : √ 3 .

Соты

Половина сот

Его можно считать переходной фазой между кубическими и ромбдодекаэдрическими сотами . ^[1] Здесь клетки окрашены в белый, красный и синий цвета в зависимости от их ориентации в пространстве. Квадратные пирамид вершины имеют укороченные грани равнобедренных треугольников, шесть из которых встречаются вместе, образуя куб. Двойник этой соты состоит из двух видов октаэдров (правильных октаэдров и треугольных антипризм), образованных путем наложения октаэдров на кубооктаэдры выпрямленного кубического сота . Обе соты имеют симметрию $[4,3,4]$ .

Поперечные сечения сот через центры ячеек образуют квадратную плитку со скошенными краями , со сплющенными горизонтальными и вертикальными шестиугольниками и квадратами на перпендикулярных многогранниках.

грани, вытянутая квадратная бипирамида может образовывать замощение пространства тетраэдрами октаэдрами и Имея правильные . (Октаэдры можно в дальнейшем разложить на квадратные пирамиды .) ^[8] Эту соту можно считать удлиненной версией тетраэдрически-октаэдрической соты .

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Кричлоу, Кейт. Порядок в космосе: справочник по дизайну . п. 46–47.
^ Гольдберг, Майкл (январь 1981 г.). «О заполняющих пространство октаэдрах». Геометрии посвященные . 10 (1): 323–335. дои : 10.1007/BF01447431 .
^ Раджваде, Арканзас (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта . Тексты и чтения по математике. Книжное агентство Индостан. п. 84–89. дои : 10.1007/978-93-86279-06-4 . ISBN 978-93-86279-06-4 .
^ Уэхара, Рюхэй (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии . Спрингер. п. 62. дои : 10.1007/978-981-15-4470-5 . ISBN 978-981-15-4470-5 . S2CID 220150682 .
^ Сапинья, Р. «Площадь и объём тела Джонсона». $J_{15}$ « . Проблемы и уравнения (на испанском языке). ISSN 2659-9899 . Проверено 9 сентября 2020 г.
^ Jump up to: Перейти обратно: ^а ^б Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .
^ Jump up to: Перейти обратно: ^а ^б Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .
^ «Соты J15» .

Внешние ссылки

Вайсштейн, Эрик В. , « Вытянутая квадратная бипирамида » (« Тело Джонсона ») в MathWorld .

[critchlow-1] Jump up to: Перейти обратно: ^а ^б Кричлоу, Кейт. Порядок в космосе: справочник по дизайну . п. 46–47.

[goldberg-2] Гольдберг, Майкл (январь 1981 г.). «О заполняющих пространство октаэдрах». Геометрии посвященные . 10 (1): 323–335. дои : 10.1007/BF01447431 .

[rajwade-3] Раджваде, Арканзас (2001). Выпуклые многогранники с условиями регулярности и третья проблема Гильберта . Тексты и чтения по математике. Книжное агентство Индостан. п. 84–89. дои : 10.1007/978-93-86279-06-4 . ISBN 978-93-86279-06-4 .

[uehara-4] Уэхара, Рюхэй (2020). Введение в вычислительное оригами: мир новой вычислительной геометрии . Спрингер. п. 62. дои : 10.1007/978-981-15-4470-5 . ISBN 978-981-15-4470-5 . S2CID 220150682 .

[pye-5] Сапинья, Р. «Площадь и объём тела Джонсона». $J_{15}$ « . Проблемы и уравнения (на испанском языке). ISSN 2659-9899 . Проверено 9 сентября 2020 г.

[berman-6] Jump up to: Перейти обратно: ^а ^б Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .

[johnson-7] Jump up to: Перейти обратно: ^а ^б Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .

[8] «Соты J15» .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v т и Твердые вещества Джонсона
Пирамиды , купола и круги	квадратная пирамида пятиугольная пирамида треугольный купол квадратный купол пятиугольный купол пятиугольная ротонда
Модифицированные пирамиды	вытянутая треугольная пирамида вытянутая квадратная пирамида вытянутая пятиугольная пирамида Гироудлиненная квадратная пирамида гироудлиненная пятиугольная пирамида треугольная бипирамида пятиугольная бипирамида вытянутая треугольная бипирамида вытянутая квадратная бипирамида вытянутая пятиугольная бипирамида гироудлиненная квадратная бипирамида
Модифицированные купола и раунды	удлиненный треугольный купол вытянутый квадратный купол удлиненный пятиугольный купол вытянутая пятиугольная ротонда гироудлинённый треугольный купол гироудлиненный квадратный купол гироудлиненный пятиугольный купол гироудлиненная пятиугольная ротонда гиробифастигий треугольный ортобикупол квадратный ортобикупол квадратный гиробикупол пятиугольный ортобикупол пятиугольный гирокупол пятиугольная ортокуполаротонда пятиугольная гирокуполаротонда пятиугольная ортобиротонда удлиненный треугольный ортобикупол удлиненный треугольный гиробикупол вытянутый квадратный гиробикупол удлиненный пятиугольный ортобикупол удлиненный пятиугольный гиробикупол вытянутая пятиугольная ортокуполаротонда вытянутая пятиугольная гирокуполаротонда вытянутая пятиугольная ортобиротонда вытянутая пятиугольная гиробиротунда гироудлиненный треугольный двуглавый купол гироудлиненный квадратный двуглавый купол гироудлиненный пятиугольный двуглавый купол гироудлинённый пятиугольный купол-ротонда гироудлиненная пятиугольная биротонда
Дополненные призмы	увеличенная треугольная призма смещенная треугольная призма триаугментированная треугольная призма увеличенная пятиугольная призма увеличенная пятиугольная призма дополненная шестиугольная призма парабиоувеличенная шестиугольная призма метаувеличенная шестиугольная призма трехугольная шестиугольная призма
Модифицированные платоновые тела	дополненный додекаэдр парабиоувеличенный додекаэдр метаувеличенный додекаэдр триаугментированный додекаэдр метабидиминированный икосаэдр трехмерный икосаэдр увеличенный трехмерный икосаэдр
Модифицированные архимедовы тела	расширенный усеченный тетраэдр дополненный усеченный куб увеличенный усеченный куб дополненный усеченный додекаэдр парабиоувеличенный усеченный додекаэдр метаувеличенный усеченный додекаэдр триаугментированный усеченный додекаэдр вращающийся ромбокосододекаэдр парабигиратный ромбикосидодекаэдр метабивративный ромбокосододекаэдр тригиратный ромбикосидодекаэдр уменьшенный ромбокосододекаэдр парагиратный уменьшенный ромбикосидодекаэдр метавращающийся уменьшенный ромбокосододекаэдр большой, уменьшенный ромбокосододекаэдр парабидиуменьшенный ромбокосододекаэдр метабидиминированный ромбикосододекаэдр вращающийся двууменьшенный ромбокосододекаэдр трехмерный ромбикосидодекаэдр
Элементарные твердые тела	курносый дисфеноид курносая квадратная антипризма сфенокорона расширенная сфенокорона сфеномегакорона Гебесфеномегакорона дисфеномен коды неисправностей треугольная гебесфеноротонда
(См. также Список твердых тел Джонсона , сортируемую таблицу)