Раздвоенный

Семья бифруста
Пример: шестиугольный бифрустум.
Лица	2 n -угольника 2 n трапеции
Края	5 н
Вершины	33н
Группа симметрии	D nh , [ n ,2], (* n 22)
Площадь поверхности	${\begin{aligned}&n(a+b){\sqrt {\left({\tfrac {a-b}{2}}\cot {\tfrac {\pi }{n}}\right)^{2}+h^{2}}}\\[2pt]&\ \ +\ n{\frac {b^{2}}{2\tan {\frac {\pi }{n}}}}\end{aligned}}$
Объем	$n{\frac {a^{2}+b^{2}+ab}{6\tan {\frac {\pi }{n}}}}h$
Двойной многогранник	Вытянутые бипирамиды
Характеристики	выпуклый

В геометрии n - угольный бифрустум — это многогранник, состоящий из трех параллельных плоскостей n -угольников , причем средняя плоскость наибольшая и обычно верхняя и нижняя конгруэнтны.

Его можно построить как две конгруэнтные усеченные пирамиды, объединенные в плоскости симметрии, а также как бипирамиду с двумя усеченными полярными вершинами.

Они являются двойниками семейства вытянутых бипирамид .

Формулы

Для правильного n -угольного бифрустума со сторонами экваториального многоугольника a , сторонами оснований боковой поверхности A l , b и полувысотой (половиной расстояния между плоскостями оснований) h площадь общая _{площадь} A и объем V равны : и $${\begin{aligned}A_{l}&=n(a+b){\sqrt {\left({\tfrac {a-b}{2}}\cot {\tfrac {\pi }{n}}\right)^{2}+h^{2}}}\\[4pt]A&=A_{l}+n{\frac {b^{2}}{2\tan {\frac {\pi }{n}}}}\\[4pt]V&=n{\frac {a^{2}+b^{2}+ab}{6\tan {\frac {\pi }{n}}}}h\end{aligned}}$$Обратите внимание, что объем V в два раза больше объема фрусты .

Формы

Три бифруста двойственны трем телам Джонсона , J _14-16 . В общем, n -угольный бифруст имеет 2 n трапеций, 2 n- угольника и двойственен вытянутым дипирамидам .

Треугольный бифрустум	Квадратный бифрустум	Пятиугольный бифрустум
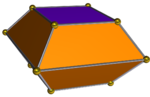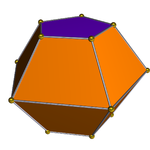6 трапеций, 2 треугольника. Двойная или вытянутая треугольная бипирамида , J 14	8 трапеций, 2 квадрата. Двойная или вытянутая квадратная бипирамида , J 15	10 трапеций, 2 пятиугольника. Двойная или вытянутая пятиугольная бипирамида , J 16.