Вытянутая бипирамида
| Вытянутая бипирамида | |
|---|---|
 Пример: вытянутая шестиугольная бипирамида. | |
| Лица | 2n треугольников n квадратов |
| Края | 5 н |
| Вершины | 2н 2 + |
| Группа симметрии | D nh , [ n ,2], (* n 22) |
| Группа вращения | Д н , [ н ,2] + , ( н 22) |
| Двойной многогранник | бифрустумы |
| Характеристики | выпуклый |
В геометрии представляют вытянутые бипирамиды собой бесконечное множество многогранников , построенных путем удлинения n- угольной бипирамиды (путем вставки n -угольной призмы между ее конгруэнтными половинками).
Существуют три вытянутые бипирамиды , являющиеся телами Джонсона :
- Вытянутая треугольная бипирамида ( J 14 ),
- Вытянутая квадратная бипирамида ( J 15 ) и
- Вытянутая пятиугольная бипирамида ( J 16 ).
Высшие формы можно построить с помощью равнобедренных треугольников .
Формы
[ редактировать ]| Имя | вытянутая треугольная бипирамида Дж 14 | вытянутая квадратная бипирамида Дж 15 | вытянутая пятиугольная бипирамида Д 16 | удлиненный шестиугольный бипирамида |
|---|---|---|---|---|
| Тип | Равносторонний | Нерегулярный | ||
| Изображение |  |  |  |  |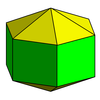
| Лица | 6 треугольников, 3 квадрата | 8 треугольников, 4 квадрата | 10 треугольников, 5 квадратов | 12 треугольников, 6 квадратов |
| Двойной | треугольный бифрустум | квадратный раздвоенный | пятиугольный бифрустум | шестиугольный бифрустум |
Приложения
[ редактировать ]Вытянутые бипирамиды иногда используются в качестве игральных костей , особенно для изготовления игральных костей с нетипичным числом сторон, например 5 или 7. На квадратных гранях таких кубиков написаны числа, которые обычно для удобства при броске увеличиваются в прямоугольники. Какое бы число не выпало лицевой стороной вверх при броске кубика, это та сторона, которую следует прочитать.
См. также
[ редактировать ]Ссылки
[ редактировать ]- Норман В. Джонсон , «Выпуклые тела с правильными гранями», Canadian Journal of Mathematics, 18 , 1966, страницы 169–200. Содержит исходное перечисление 92 тел и гипотезу об отсутствии других.
- Виктор А. Залгаллер (1969). Выпуклые многогранники с правильными гранями . Консультантское бюро. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.
 | Эта многогранникам, статья, посвященная незавершена . Вы можете помочь Википедии, расширив ее . |