Уменьшенный трапецоэдр
| Уменьшенный трапецоэдр | |
|---|---|
 Пример квадратной формы | |
| Лица | н воздушные змеи n треугольников 1 н -гон |
| Края | 4 n |
| Вершины | 2н 1 + |
| Группа симметрии | C nv , [n], (*nn) |
| Группа вращения | С н , [н] + , (нн) |
| Двойной многогранник | самодвойственный |
| Характеристики | выпуклый |
В геометрии — уменьшенный трапецоэдр это многогранник в бесконечном множестве многогранников, построенный путем удаления одной из полярных вершин трапецоэдра и замены ее новой гранью ( уменьшение ). У него есть одна правильная n -угольная базовая грань, n треугольных граней вокруг основания и n воздушных змеев , сходящихся наверху. Воздушных змеев также можно заменить ромбами определенных пропорций.
Наряду с множеством пирамид и вытянутыми пирамидами эти фигуры топологически самодвойственны .
Ее также можно рассматривать как расширенную n -угольную антипризму с n -угольной пирамидой, добавленной к одной из n -угольных граней, и высота которой отрегулирована так, чтобы верхние треугольные грани антипризмы можно было сделать коппараллельными граням пирамиды и объединить их. в лица в форме воздушного змея.
Они также связаны с гировытянутыми пирамидами как дополненные антипризмы и являются телами Джонсона для n = 4, 5 . В этой последовательности вместо граней воздушного змея есть наборы из двух треугольников.
Примеры
[ редактировать ]| Симметрия | С 3В | С 4В | С 5В | С 6в | С 7В | С 8в ... | |
|---|---|---|---|---|---|---|---|
| Изображение |  |  |  |  |  | ||
| ромбический форма |  |  |  |  |  |  | |
| Сеть |  |  |  |  |  |  | |
| Лица | 3 трапеции 3+1 треугольников | 4 трапеции 4 треугольника 1 квадрат | 5 трапеций 5 треугольников 1 пятиугольник | 6 трапеций 6 треугольников 1 шестиугольник | 7 трапеций 7 треугольников 1 семиугольник | 8 трапеций 7 треугольников 1 восьмиугольник | |
| Края | 12 | 16 | 20 | 24 | 28 | 32 | |
| Вершины | 7 | 9 | 11 | 13 | 15 | 17 | |
| Трапезоэдры | |||||||
| Симметрия | Д 3д | Д 4д | Д 5д | Д 6д | Д 7д | DD8d | |
| Изображение |  3 | 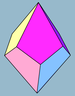 4 | 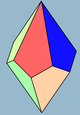 5 | 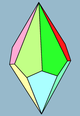 6 | |||
| Лица | 3+3 ромба (Или квадраты) | 4+4 воздушных змея | 5+5 воздушных змеев | 6+6 воздушных змеев | 7+7 воздушных змеев | ||
| Края | 12 | 16 | 20 | 24 | 28 | ||
| Вершины | 8 | 10 | 12 | 14 | 16 | ||
| Гироудлиненная пирамида или (расширенные антипризмы) | |||||||
| Симметрия | С 3В | С 4В | С 5В | С 6в | С 7В | С 8В | |
| Изображение |  3 |  4 |  5 | 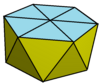 6 | |||
| Лица | 9+1 треугольников | 12 треугольников 1 квадрат | 15 треугольников 1 пятиугольник | 18 треугольников 1 шестиугольник | |||
Особые случаи
[ редактировать ]Есть три особых случая геометрии уменьшенного тригонального трапецоэдра . Самый простой — уменьшенный куб . Честаэдр . , названный в честь художника Фрэнка Честера , построен с равносторонними треугольниками вокруг основания, а геометрия скорректирована таким образом, чтобы грани воздушного змея имели ту же площадь, что и равносторонние треугольники [1] [2] Последнее можно увидеть, увеличив правильный тетраэдр и октаэдр , оставив 10 равносторонних треугольных граней, а затем объединив 3 набора сопараллельных равносторонних треугольных граней в 3 (60 градусов) ромбические грани. Его также можно рассматривать как тетраэдр, у которого 3 из 4 вершин спрямлены . Три ромбические грани складываются плоско, образуя половину гексаграммы .
| Топология семигранника № 31 Уменьшенный куб | Честаэдр (лица равной площади) | Дополненный октаэдр (Равносторонние лица) |
|---|---|---|
 |  | 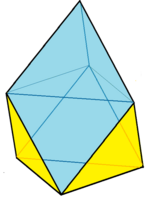 |
 | 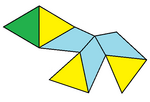 |  |
| 3 квадрата 3 треугольника 45-45-90 1 равносторонняя треугольная грань | 3 лица воздушного змея 3+1 грани равностороннего треугольника | 3 ромбические грани по 60 градусов 3+1 грани равностороннего треугольника |
См. также
[ редактировать ]- Вытянутая пирамида
- Гироудлиненная бипирамида
- Вытянутая бипирамида
- Гироудлиненная пирамида
- Тетраэдрически уменьшенный додекаэдр
Ссылки
[ редактировать ]- ^ «Геометрия Честаэдра» . Искусство и наука Фрэнка Честера . Проверено 22 января 2020 г.
- ^ Донке, Ханс-Йоаким (март 2011 г.). «Преобразование тетраэдра в честаэдр» . Вольфрам Альфа . Архивировано из оригинала 7 октября 2014 г. Проверено 22 января 2020 г.