семигранник

Семигранник имеющий ( мн.: гептаэдры ) — многогранник, семь сторон или граней .
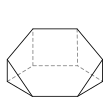
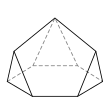
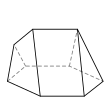
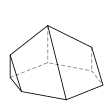
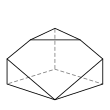
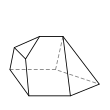
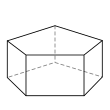
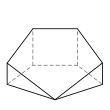
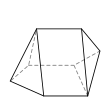
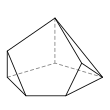
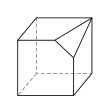
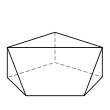
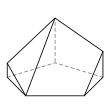
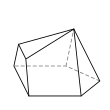
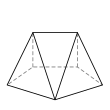
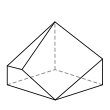
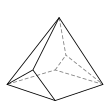
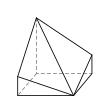
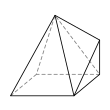
Семигранник может принимать большое количество различных основных форм или топологий. Наиболее знакомыми являются шестиугольная пирамида и пятиугольная призма . Также следует отметить тетрагемигексаэдр , который можно рассматривать как мозаику реальной проективной плоскости . Ни один семигранник не является правильным .
Топологически отличный семигранник
[ редактировать ]Выпуклый
[ редактировать ]Существует 34 топологически различных выпуклых семигранника, не считая зеркальных изображений. [2] (Два многогранника «топологически различны», если они имеют существенно различное расположение граней и вершин, так что невозможно исказить один в другой, просто изменяя длины ребер или углы между ребрами или гранями.)
Ниже изображен пример каждого типа вместе с количеством сторон на каждой из граней. Изображения упорядочены по убыванию количества шестисторонних граней (если есть), за которыми следует убывание количества пятисторонних граней (если есть) и так далее.
Вогнутый
[ редактировать ]Шесть топологически различных вогнутых семигранников (исключая зеркальные изображения) можно образовать путем объединения двух тетраэдров в различных конфигурациях. Третий, четвертый и пятый из них имеют грань с коллинеарными смежными краями, а шестой имеет грань, которая не является односоединенной . [ нужна ссылка ] | |
  13 топологически различных семигранников (исключая зеркальные изображения) можно образовать, вырезав вырезы на краях треугольной призмы или квадратной пирамиды. Показаны два примера. |   разнообразные неодносвязные Возможны семигранники. Показаны два примера. [ нужна ссылка ] |
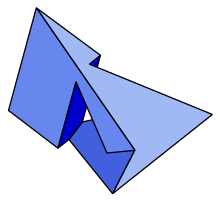
Одним из особенно интересных примеров является многогранник Силасси , тороидальный многогранник с семью невыпуклыми шестигранными гранями. [3]
Ссылки
[ редактировать ]- ^ Фрэнк Честер. «Геометрия Честаэдра» . Проверено 8 августа 2022 г.
- ^ «Счет многогранников» . numericana.com . 5 апреля 2015 г.
- ^ Силасси, Лайош (1986), «Регулярные тороиды» (PDF) , Структурная топология , 13 : 69–80
Внешние ссылки
[ редактировать ]- Многогранники с 4–7 гранями , Стивен Датч
- Вайсштейн, Эрик В. «Гептаэдр» . Математический мир .