Тридекаэдр
| Общие тридекаэдры | |
|---|---|
 Тридекаэдр, заполняющий пространство | 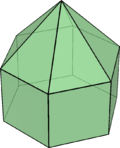 Вытянутая шестиугольная пирамида |
 Шестнадцатиугольная призма |  Гироудлиненная квадратная пирамида |
Тридекаэдр трискадекаэдр , или многогранник , представляет собой с тринадцатью гранями . Существует множество топологически различных форм тридекаэдра, например двенадцатиугольная пирамида и десятиугольная призма . Однако тридекаэдр не может быть правильным многогранником, поскольку не существует правильного многоугольника, который мог бы образовать правильный тридекаэдр, а известны только пять правильных выпуклых многогранников. [примечания 1] [1]
Выпуклый
[ редактировать ]Существует 96 262 938 топологически различных выпуклых тридекаэдров, исключая зеркальные изображения, имеющих не менее 9 вершин. [2] (Два многогранника «топологически различны», если они имеют существенно различное расположение граней и вершин, так что невозможно исказить один в другой, просто изменяя длины ребер или углы между ребрами или гранями.) Существует псевдо - заполняющий пространство тридекаэдр , способный заполнить все трехмерное пространство вместе со своим зеркальным отражением. [3]
Общие тридекаэдры
[ редактировать ]Примеры
[ редактировать ]| Имя ( расположение вершин ) | Символ | Стереограмма | Расширенный вид | Лица | Края | Апексы | |
|---|---|---|---|---|---|---|---|
| Шестнадцатиугольная призма | т{2,11} {11}х{} |  | 13 | квадрат × 11 Hendecagon × 2 | 33 | 22 | |
| Двенадцатиугольная пирамида | ( )∨{12} |  | 13 | треугольник × 12 двенадцатиугольник × 1 | 24 | 13 | |
| Вытянутая шестиугольная пирамида |  | 13 | треугольник × 6 квадрат × 6 шестиугольник × 1 | 24 | 13 | ||
| Тридекаэдр, заполняющий пространство |  |  | 13 | четырехугольник × 6 пятиугольник × 6 шестиугольник × 1 | 30 | 19 | |
| Гироудлиненная квадратная пирамида |  |  | 13 | треугольник × 12 квадрат × 1 | 20 | 9 | |
| усеченный шестиугольный трапоэдр |  | 13 | 1 шестигранное основание 6 пятиугольника сторон 6 кайта сторон | 30 | 19 | ||
| Биувеличенная пятиугольная призма |  | 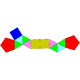 | 13 | треугольник × 8 квадрат × 3 пятиугольник × 2 | 23 | 12 | |
Шестнадцатиугольная призма
[ редактировать ]
Пятиугольная призма — это призма с основанием из пятиугольника . Это разновидность тридекаэдра, состоящего из 13 граней, 22 вершин и 33 сторон. Правильная девятиугольная призма — это пятнадцатиугольная призма, грани которой представляют собой правильные пятнадцатиугольники, а каждая ее вершина является общей вершиной 2 квадратов и одного шестнадцатиугольника. В вершинной фигуре шестиугольная призма изображается ; в обозначениях Шлефли его можно представить как {11}×{} или t{2, 11}; ![]()
![]()
![]()
![]()
![]()
![]() можно использовать в диаграмме Кокстера-Динкина для его представления ; его символ Витгофа — 2 11 | 2; в обозначениях многогранников Конвея его можно представить как P11. Если длина стороны основания правильной девятиугольной призмы равна и высота , то его объем и площадь поверхности являются: [4]
можно использовать в диаграмме Кокстера-Динкина для его представления ; его символ Витгофа — 2 11 | 2; в обозначениях многогранников Конвея его можно представить как P11. Если длина стороны основания правильной девятиугольной призмы равна и высота , то его объем и площадь поверхности являются: [4]
Двенадцатиугольная пирамида
[ редактировать ]
– Двенадцатиугольная пирамида это пирамида с двенадцатиугольным основанием . Это тип тридекаэдра, который имеет 13 граней , 24 ребра и 13 вершин , а его двойственный многогранник является самим собой. [5] Правильная двенадцатиугольная пирамида – это двенадцатиугольная пирамида, основанием которой является правильный двенадцатиугольник. Если длина стороны основания правильной двенадцатигранной пирамиды равна и высота , то его объем и площадь поверхности являются: [5]
Тридекаэдр, заполняющий пространство
[ редактировать ]| Тридекаэдр, заполняющий пространство | |
|---|---|
 | |
| Тип | 6 трапеций 6 пятиугольников 1 правильный шестиугольник |
| Лица | 13 |
| Края | 30 |
| Вершины | 19 |
. Тридекаэдр, заполняющий пространство [6] [7] представляет собой тридекаэдр, способный полностью заполнить трехмерное пространство, не оставляя пробелов. У него 13 граней, 30 ребер и 19 вершин . Среди тринадцати граней шесть трапеций , шесть пятиугольников и один правильный шестиугольник . [8]
- Двойной многогранник
многогранника Двойной многогранник — это эннеадекаэдр . Он похож на скрученный полукуб, но перед скручиванием одна из его вершин рассматривается как грань.
| Изображение | Анимация вращения | Расширенный вид | |
|---|---|---|---|
| Оригинальный многогранник тридекаэдр |  |  |  |
| Двойной многогранник эннеадекаэдр |  |  | 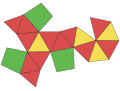 |
Примечания
[ редактировать ]- ^ Даже если бы было 13 конгруэнтных граней, это все равно не считалось бы правильным многогранником. Помимо того, что все грани правильного многогранника равны, углы и стороны на каждой грани должны быть равны по размеру. Этому условию удовлетворяют только правильные многоугольники, а вот грани тринадцатигранной формы — нет, поэтому правильного тридекаэдра быть не может.
Ссылки
[ редактировать ]- ^ доказательство платоновых тел . Архивировано 21 ноября 2015 г. на сайте Wayback Machine mathsisfun.com [2016-1-10]
- ^ Подсчет многогранников
- ^ Людасер, Рэнди. «Соты и структурный дизайн упаковки: больше способов занять пространство» . Пляжный брендинг и дизайн упаковки . Архивировано из оригинала 7 марта 2016 г.
- ^ «Призма Гендекагона» . Сайт Вольфрам Альфа .
- ^ Jump up to: Перейти обратно: а б «Пирамида Додекагона» . Сайт Вольфрам Альфа .
- ↑ Сплюснутые ромбоэдры . Архивировано 21 сентября 2016 г. на сайте Wayback Machine science.unitn.it [10 января 2016 г.]
- ^ Виртуальные многогранники, греческие числовые префиксы. Архивировано 15 января 2016 г. на Wayback Machine , 1996, Джордж В. Харт, georgehart.com [10 января 2016 г.]
- ↑ Заполняющий пространство многогранник с 13 гранями. Архивировано 1 июля 2017 г. на сайте Wayback Machine science.unitn.it [10.01.2016].
Внешние ссылки
[ редактировать ]- Самодвойственные тридекаэдры
- Что такое многогранники? , с греческими цифровыми префиксами








