Параллелепипед

Параллелепипед
Тип	Призма Плесоэдр
Лица	6 параллелограммов
Края	12
Вершины	8
Группа симметрии	С я , [2 + ,2 + ], (×), порядок 2
Характеристики	выпуклый, зоноэдр

В геометрии параллелепипед образованная — объёмная фигура, шестью параллелограммами термин ромбовидный ( в этом значении иногда употребляют также ). По аналогии, оно относится к параллелограмму так же, как куб относится к квадрату .

Три эквивалентных определения параллелепипеда :

• шестигранник с тремя парами параллельных граней,
• многогранник ), каждая из с шестью гранями ( шестигранник которых является параллелограммом, и
• призма , основанием которой является параллелограмм .

Прямоугольный кубоид (шесть прямоугольных граней), куб (шесть квадратных граней) и ромбоэдр (шесть ромбических граней) — все это частные случаи параллелепипеда.

«Параллепипед» сейчас обычно произносится / ˌ p ær ə ˌ l ɛ l ɪ ˈ p ɪ p ɪ d / или / ˌ p ær ə ˌ l ɛ l ɪ ˈ p aɪ p ɪ d / ; традиционно это / ˌ p ær ə lel ep ped ˈ ɪ -ə - ped -ih - / PARR lel- EP было несмотря на его этимологию в греческом языке παραλληλεπίπεδον параллелепипед , тело, «имеющее параллельные плоскости».

Параллелепипеды — подкласс призматоидов .

Свойства

Любую из трёх пар параллельных граней можно рассматривать как базовые плоскости призмы. Параллелепипед имеет три набора по четыре параллельных ребра; ребра внутри каждого набора имеют одинаковую длину.

Параллелепипеды возникают в результате линейных преобразований куба . (для невырожденных случаев: биективных линейных преобразований)

Поскольку каждая грань обладает точечной симметрией , параллелепипед является зоноэдром . Также весь параллелепипед имеет точечную симметрию C _i (см. также триклинику ). Каждое лицо, если смотреть снаружи, является зеркальным отражением противоположного лица. Грани в целом хиральны , а параллелепипед — нет.

возможна Заполняющая пространство мозаика с конгруэнтными копиями любого параллелепипеда.

Объем

Параллелепипед, порожденный тремя векторами

Параллелепипед – это призма в основании которой находится параллелограмм , .Отсюда и объем $V$ параллелепипеда есть произведение площади основания $B$ и высота $h$ (см. схему). С

• $B=\left|\mathbf {a} \right|\cdot \left|\mathbf {b} \right|\cdot \sin \gamma =\left|\mathbf {a} \times \mathbf {b} \right|$ (где $\gamma$ угол между векторами $\mathbf {a}$ и $\mathbf {b}$), и
• $h=\left|\mathbf {c} \right|\cdot \left|\cos \theta \right|$ (где $\theta$ угол между вектором $\mathbf {c}$ и нормаль к основанию), получим:

$$V=B\cdot h=\left(\left|\mathbf {a} \right|\left|\mathbf {b} \right|\sin \gamma \right)\cdot \left|\mathbf {c} \right|\left|\cos \theta \right|=\left|\mathbf {a} \times \mathbf {b} \right|\left|\mathbf {c} \right|\left|\cos \theta \right|=\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|.$$

Смешанное произведение трех векторов называется тройным произведением . Его можно описать определителем . Следовательно, для $\mathbf {a} =(a_{1},a_{2},a_{3})^{\mathsf {T}},~\mathbf {b} =(b_{1},b_{2},b_{3})^{\mathsf {T}},~\mathbf {c} =(c_{1},c_{2},c_{3})^{\mathsf {T}},$ объем:

$$V=\left|\det {\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right|.$$

( В1 )

Другой способ доказать ( V1 ) — использовать скалярную составляющую в направлении $\mathbf {a} \times \mathbf {b}$ вектора $\mathbf {c}$:

$${\begin{aligned}V=\left|\mathbf {a} \times \mathbf {b} \right|\left|\operatorname {scal} _{\mathbf {a} \times \mathbf {b} }\mathbf {c} \right|=\left|\mathbf {a} \times \mathbf {b} \right|{\frac {\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|}{\left|\mathbf {a} \times \mathbf {b} \right|}}=\left|\left(\mathbf {a} \times \mathbf {b} \right)\cdot \mathbf {c} \right|.\end{aligned}}$$

Результат следующий.

Альтернативное представление объема использует только геометрические свойства (углы и длины ребер):

$$V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}},$$

( В2 )

где $\alpha =\angle (\mathbf {b} ,\mathbf {c} )$, $\beta =\angle (\mathbf {a} ,\mathbf {c} )$, $\gamma =\angle (\mathbf {a} ,\mathbf {b} )$, и $a,b,c$ — длины ребер.

Доказательство ( V2 )

Доказательство ( V2 ) использует свойства определителя и геометрическую интерпретацию скалярного произведения :

Позволять $M$ — матрица размера 3×3, столбцами которой являются векторы $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$ (см. выше). Тогда верно следующее:

$${\begin{aligned}V^{2}&=\left(\det M\right)^{2}=\det M\det M=\det M^{\mathsf {T}}\det M=\det(M^{\mathsf {T}}M)\\&=\det {\begin{bmatrix}\mathbf {a} \cdot \mathbf {a} &\mathbf {a} \cdot \mathbf {b} &\mathbf {a} \cdot \mathbf {c} \\\mathbf {b} \cdot \mathbf {a} &\mathbf {b} \cdot \mathbf {b} &\mathbf {b} \cdot \mathbf {c} \\\mathbf {c} \cdot \mathbf {a} &\mathbf {c} \cdot \mathbf {b} &\mathbf {c} \cdot \mathbf {c} \end{bmatrix}}\\&=\ a^{2}\left(b^{2}c^{2}-b^{2}c^{2}\cos(\alpha )\right)\\&\quad -ab\cos(\gamma )\left(ab\cos(\gamma )c^{2}-ac\cos(\beta )\;bc\cos(\alpha )\right)\\&\quad +ac\cos(\beta )\left(ab\cos(\gamma )bc\cos(\alpha )-ac\cos(\beta )b^{2}\right)\\&=\ a^{2}b^{2}c^{2}-a^{2}b^{2}c^{2}\cos(\alpha )\\&\quad -a^{2}b^{2}c^{2}\cos ^{2}(\gamma )+a^{2}b^{2}c^{2}\cos(\alpha )\cos(\beta )\cos(\gamma )\\&\quad +a^{2}b^{2}c^{2}\cos(\alpha )\cos(\beta )\cos(\gamma )-a^{2}b^{2}c^{2}\cos(\beta )\\&=\ a^{2}b^{2}c^{2}\left(1-\cos ^{2}(\alpha )-\cos ^{2}(\gamma )+\cos(\alpha )\cos(\beta )\cos(\gamma )+\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\beta )\right)\\&=\ a^{2}b^{2}c^{2}\;\left(1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\right).\end{aligned}}$$

(Последние шаги используют $\mathbf {a} \cdot \mathbf {a} =a^{2}$, ..., $\mathbf {a} \cdot \mathbf {b} =ab\cos \gamma$, $\mathbf {a} \cdot \mathbf {c} =ac\cos \beta$, $\mathbf {b} \cdot \mathbf {c} =bc\cos \alpha$, ...)

Соответствующий тетраэдр

Объем любого тетраэдра , имеющего три сходящихся ребра параллелепипеда, равен одной шестой объема этого параллелепипеда (см. доказательство ).

Площадь поверхности

Площадь поверхности параллелепипеда равна сумме площадей ограничивающих его параллелограммов:

$${\begin{aligned}A&=2\cdot \left(|\mathbf {a} \times \mathbf {b} |+|\mathbf {a} \times \mathbf {c} |+|\mathbf {b} \times \mathbf {c} |\right)\\&=2\left(ab\sin \gamma +bc\sin \alpha +ca\sin \beta \right).\end{aligned}}$$

(Информацию о маркировке см. в предыдущем разделе.)

Особые

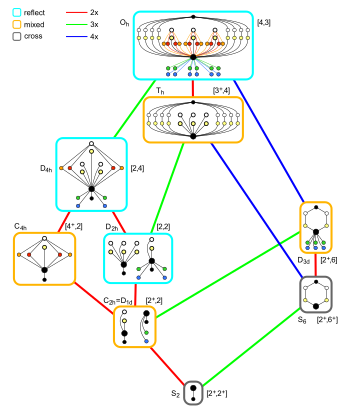Отношения подгруппы октаэдрической симметрии с центром инверсии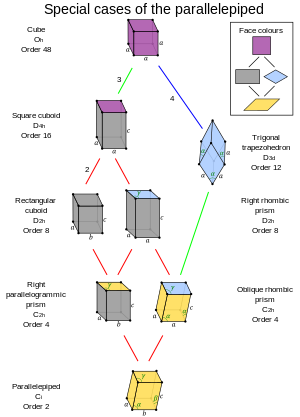

Частные случаи параллелепипеда

Форма	Куб	Квадратный кубоид	Трехугольный трапецоэдр	Прямоугольный кубоид	Правая ромбическая призма	Правая параллелограммная призма	Косая ромбическая призма
Ограничения	$a=b=c$ $\alpha =\beta =\gamma =90^{\circ }$	$a=b$ $\alpha =\beta =\gamma =90^{\circ }$	$a=b=c$ $\alpha =\beta =\gamma$	$\alpha =\beta =\gamma =90^{\circ }$	$a=b$ $\alpha =\beta =90^{\circ }$	$\alpha =\beta =90^{\circ }$	$a=b$ $\alpha =\beta$
Симметрия	Ой ​ заказать 48	Д 4 часа заказать 16	Д 3д заказать 12	Д 2 часа заказать 8		С 2 часа заказать 4
Изображение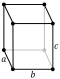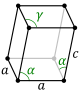
Лица	6 квадратов	2 квадрата, 4 прямоугольника	6 ромбов	6 прямоугольников	4 прямоугольника, 2 ромба	4 прямоугольника, 2 параллелограмма	2 ромба 4 параллелограмма

• Параллелепипед с симметрией Oh _{известен} как куб , имеющий шесть равных квадратных граней.
• Параллелепипед с симметрией D _4h известен как квадратный кубоид , который имеет две квадратные грани и четыре конгруэнтные прямоугольные грани.
• Параллелепипед с симметрией D _3d известен как тригональный трапецоэдр , имеющий шесть конгруэнтных ромбических граней (также называемый изоэдральным ромбоэдром ).
• Для параллелепипедов с симметрией D _2h возможны два случая:
  • Прямоугольный кубоид : имеет шесть прямоугольных граней (также называемый прямоугольным параллелепипедом или иногда просто кубоидом ).
  • Правая ромбическая призма : имеет две ромбические грани и четыре равных прямоугольных грани.

    Примечание: полностью ромбический особый случай с двумя ромбическими гранями и четырьмя конгруэнтными квадратными гранями. $(a=b=c)$, имеет то же имя и ту же группу симметрии (D _2h , порядок 8).

• Для параллелепипедов с симметрией C _2h возможны два случая:
  • Призма правая параллелограммная : имеет четыре прямоугольные грани и две параллелограммные грани.
  • Косая ромбическая призма : у нее две ромбические грани, причем из остальных граней две соседние равны, а две другие тоже (две пары являются зеркальным отражением друг друга).

Идеальный параллелепипед

Совершенный параллелепипед — это параллелепипед с ребрами целой длины, гранями и пространственными диагоналями . В 2009 году было показано существование десятков идеальных параллелепипедов. отвечая на открытый вопрос Ричарда Гая . В одном примере есть ребра 271, 106 и 103, диагонали второстепенных граней 101, 266 и 255, большие диагонали граней 183, 312 и 323 и пространственные диагонали 374, 300, 278 и 272.

Известны совершенные параллелепипеды, имеющие две прямоугольные грани. Но неизвестно, существуют ли такие, у которых все лица прямоугольные; такой случай можно было бы назвать идеальным кубоидом .

Параллелотоп

Коксетер назвал обобщение параллелепипеда в высших измерениях параллелотопом . В современной литературе термин «параллелепипед» часто используется и в более высоких (или произвольных конечных) измерениях.

Конкретно в n -мерном пространстве его называют n -мерным параллелотопом или просто n -параллелотопом (или n -параллелепипедом). Таким образом, параллелограмм — это 2-параллелоэдр, а параллелепипед — 3-параллелоэдр.

Диагонали . n пополам -параллелоэдра пересекаются в одной точке и делятся этой точкой Инверсия в этой точке оставляет n -параллелотоп неизменным. См. также Неподвижные точки групп изометрий в евклидовом пространстве .

Ребра, исходящие из одной вершины k -параллелоэдра, образуют k -шкалу. $(v_{1},\ldots ,v_{n})$ векторного пространства, и параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1.

-объем n n -параллелотопа , вложенного в $\mathbb {R} ^{m}$ где $m\geq n$ можно вычислить с помощью определителя Грама . Альтернативно, объем является нормой внешнего произведения векторов:

$$V=\left\|v_{1}\wedge \cdots \wedge v_{n}\right\|.$$

Если m = n , это равно абсолютному значению определителя матрицы, образованной компонентами n векторов.

Формула для вычисления объема n -параллелотопа P в $\mathbb {R} ^{n}$, чьи n + 1 вершины $V_{0},V_{1},\ldots ,V_{n}$, является

$$\mathrm {Vol} (P)=\left|\det \left(\left[V_{0}\ 1\right]^{\mathsf {T}},\left[V_{1}\ 1\right]^{\mathsf {T}},\ldots ,\left[V_{n}\ 1\right]^{\mathsf {T}}\right)\right|,$$

где $[V_{i}\ 1]$ — вектор-строка, образованный конкатенацией компонентов $V_{i}$ и 1.

Аналогично, объем любого n - симплекса , имеющего n сходящихся ребер параллелоэдра, имеет объем, равный одному 1/ n ! объема этого параллелоэдра.

Этимология

Термин параллелепипед происходит от древнегреческого παραλληλεπίπεδον ( parallēlepípedon , «тело с параллельными плоскими поверхностями»), от parallēl («параллельный») + epípedon («плоская поверхность»), от epí- («на») + pedon («земля»). ). Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.

На английском языке термин «параллелипедон» засвидетельствован в переводе Начал» Евклида « Генри Биллингсли в 1570 году . Написание параллелепипед используется в издании 1644 года Пьера Эригона «Курса математики» . В 1663 году современный параллелепипед засвидетельствован в Уолтера Чарлтона «Хорее гигантской» .

В словаре Чарльза Хаттона (1795 г.) показаны параллелепипед и параллелопипедон , показывая влияние объединяющей формы параллело- , как если бы вторым элементом был пипдон, а не эпипедон . Ной Вебстер (1806 г.) включает в себя написание «параллелепипед» . 1989 года В Оксфордском словаре английского языка ) явно описывается параллелепипед (и параллелепипед только произношения с ударением на пятый слог пи ( /paɪ/ как неправильные формы, но в издании 2004 года они перечислены без комментариев, и даны ).

См. также

• Списки фигур

Ссылки

• Коксетер, Правильные многогранники HSM , 3-е изд. Нью-Йорк: Дувр, с. 122, 1973. (Он определяет параллелотоп как обобщение параллелограмма и параллелепипеда в n-мерностях.)

Внешние ссылки

• Вайсштейн, Эрик В. «Параллелепипед» . Математический мир .
• Вайсштейн, Эрик В. «Параллелотоп» . Математический мир .
• Бумажная модель параллелепипеда (сетка)