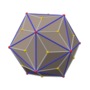
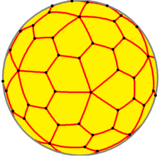
Пятиугольный шестиконтаэдр

Пятиугольный шестиконтаэдр
(Нажмите здесь, чтобы увидеть вращающуюся модель)
Тип	Каталонский солид
Диаграмма Кокстера
Обозначение Конвея	гД
Тип лица	В3.3.3.3.5 неправильный пятиугольник
Лица	60
Края	150
Вершины	92
Вершины по типу	12 {5} 20+60 {3}
Группа симметрии	я , 1/2 5,3 3 Ч _] , [ ⁺, (532)
Группа ротации	Я, [5,3] ⁺, (532)
Двугранный угол	153°10′43″
Характеристики	выпуклый, гране-транзитивный хиральный
Курносый додекаэдр ( двойной многогранник )	Сеть

В геометрии пятиугольный шестиконтаэдр — каталанское тело , двойственное курносому додекаэдру . Он имеет две различные формы, которые являются зеркальными отражениями (или « энантиоморфами ») друг друга. Он имеет 92 вершины, охватывающие 60 пятиугольных граней. Это каталонское тело с наибольшим количеством вершин. Среди каталонских и архимедовых тел он занимает второе место по количеству вершин после усеченного икосододекаэдра , имеющего 120 вершин.

Декартовы координаты [ править ]

Использование икосаэдрической симметрии орбит Вейля $O(\Lambda )=W(H_{3})/C_{2}\approx A_{5}$ порядка 60 ^[1] дает следующие декартовы координаты с $\phi ={\frac {1+{\sqrt {5}}}{2}}$ это золотое сечение :

Двенадцать вершин правильного икосаэдра с единичным радиусом описанной окружности с центром в начале координат и координатами ${\frac {(0,\pm 1,\pm \phi )}{\sqrt {\phi ^{2}+1}}},{\frac {(\pm 1,\pm \phi ,0)}{\sqrt {\phi ^{2}+1}}},{\frac {(\pm \phi ,0,\pm 1)}{\sqrt {\phi ^{2}+1}}}.$
Двадцать вершин правильного додекаэдра с единичным радиусом описанной окружности с центром в начале координат, масштабированные с коэффициентом $R\approx 0.95369785218$ от точного решения уравнения $700569-1795770x^{2}+1502955x^{4}-423900x^{6}+14175x^{8}-2250x^{10}+125x^{12}=0$ , что дает координаты

(\pm 1,\pm 1,\pm 1){\frac {R}{\sqrt {3}}}

и

(0,\pm \phi ,\pm {\frac {1}{\phi }}){\frac {R}{\sqrt {3}}},(\pm {\frac {1}{\phi }},0,\pm \phi ){\frac {R}{\sqrt {3}}},(\pm \phi ,\pm {\frac {1}{\phi }},0){\frac {R}{\sqrt {3}}}.

с единичным радиусом описанной окружности, Шестьдесят вершин кирального курносого додекаэдра масштабированного на $R$ . Имеется пять наборов по двенадцать вершин, все с четными перестановками (т.е. с сигнатурой четности =1).

Группа из двух наборов по двенадцать имеет 0 или 2 знака минус (т. е. 1 или 3 знака плюс):

(\pm 0.267979,\pm 0.881108,\pm 0.389662)R,

(\pm 0.721510,\pm 0.600810,\pm 0.344167)R,

и еще одна группа из трех наборов по 12 цифр имеет 0 или 2 знака плюс (т. е. 1 или 3 знака минус):

(\pm 0.176956,\pm 0.824852,\pm 0.536941)R,

(\pm 0.435190,\pm 0.777765,\pm 0.453531)R,

(\pm 0.990472,\pm 0.103342,\pm 0.091023)R.

Отрицание всех вершин в обеих группах дает зеркало кирального курносого додекаэдра, но приводит к той же выпуклой оболочке пятиугольного гексеконтаэдра.

Строительство [ править ]

Пятиугольный гексеконтаэдр можно построить из курносого додекаэдра, не принимая двойственный. К 12 пятиугольным граням курносого додекаэдра добавляются пятиугольные пирамиды, а к 20 треугольным граням, не имеющим общего ребра с пятиугольником, добавляются треугольные пирамиды. Высоты пирамид отрегулированы так, чтобы они были копланарны с другими 60 треугольными гранями курносого додекаэдра. В результате получается пятиугольный шестиконтаэдр. ^[2]

Альтернативный метод построения использует кватернионы и икосаэдрическую симметрию орбит группы Вейля . $O(\Lambda )=W(H_{3})/C_{2}\approx A_{5}=I$ порядка 60. ^[3] Это показано на рисунке справа.

В частности, с кватернионами из бинарной группы икосаэдра. $(p,q)\in I_{h}$ , где $q={\bar {p}}$ является сопряженным $p$ и $[p,q]:r\rightarrow r'=prq$ и $[p,q]^{*}:r\rightarrow r''=p{\bar {r}}q$ , то так же, как группа Кокстера $W(H_{4})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace$ – группа симметрии 600-ячейки и 120-ячейки порядка 14400, имеем $W(H_{3})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace =A_{5}\times C_{2}=I_{h}$ порядка 120. $I$ определяется как четные перестановки $I_{h}$ такой, что $[I,{\bar {I}}]:r$ дает 60 координат скрученного кирального курносого додекаэдра, где $r\approx -0.389662e_{1}+0.267979e_{2}-0.881108e_{3}$ — это одна перестановка из первого набора из 12 перечисленных выше . Точные координаты для $r$ получается, если принять решение $x^{3}-x^{2}-x-\phi =0$ , с $x\approx 1.94315$ и применяя его к нормализации $r=(-1+x^{2}(-1-2/\phi -x\phi )e_{1}+(3-x^{2}+3x\phi )e_{2}+((x^{3}-1/\phi )\phi ^{3})e_{3}$ .

Геометрия [ править ]

Грани представляют собой неправильные пятиугольники с двумя длинными и тремя короткими сторонами. Позволять $\xi \approx 0.943\,151\,259\,24$ быть действительным нулем многочлена $x^{3}+2x^{2}-\phi ^{2}$ .Тогда соотношение $l$ длин ребер определяется выражением:

l={\frac {1+\xi }{2-\xi ^{2}}}\approx 1.749\,852\,566\,74

.

Грани имеют четыре равных тупых угла и один острый угол (между двумя длинными гранями). Тупые углы равны $\arccos(-\xi /2)\approx 118.136\,622\,758\,62^{\circ }$ , а острый равен $\arccos(-\phi ^{2}\xi /2+\phi )\approx 67.453\,508\,965\,51^{\circ }$ . Двугранный угол равен $\arccos(-\xi /(2-\xi ))\approx 153.178\,732\,558\,45^{\circ }$ .Заметим, что центры граней курносого додекаэдра не могут служить непосредственно вершинами пятиугольного шестиконтаэдра: четыре центра треугольника лежат в одной плоскости, а центр пятиугольника - нет; его необходимо вытолкнуть радиально, чтобы он стал компланарным центрам треугольников. Следовательно, вершины пятиугольного шестиконтаэдра не все лежат на одной сфере и по определению он не является зоноэдром .

Чтобы найти объем и площадь поверхности пятиугольного шестиконтаэдра, обозначим меньшую сторону одной из пятиугольных граней как $b$ и установим константу t ^[4]

$t={\frac {{\sqrt[{3}]{44+12\phi (9+{\sqrt {81\phi -15}})}}+{\sqrt[{3}]{44+12\phi (9-{\sqrt {81\phi -15}})}}-4}{12}}\approx 0.471\,575\,629\,622$ .

Тогда площадь поверхности (А) равна:

$A={\frac {30b^{2}\cdot (2+3t)\cdot {\sqrt {1-t^{2}}}}{1-2t^{2}}}\approx 162.698\,964\,198b^{2}$ .

А объем (V):

$V={\frac {5b^{3}(1+t)(2+3t)}{(1-2t^{2})\cdot {\sqrt {1-2t}}}}\approx 189.789\,852\,067b^{3}$ .

Используя их, можно вычислить меру сферичности этой формы:

\Psi ={\frac {\pi ^{\frac {1}{3}}(6V)^{\frac {2}{3}}}{A}}\approx 0.98163

Вариации [ править ]

Изоэдральные варианты могут быть построены с пятиугольными гранями с тремя длинами ребер.

Этот показанный вариант можно построить путем добавления пирамид к 12 пятиугольным граням и 20 треугольным граням курносого додекаэдра так, чтобы новые треугольные грани были сопараллельны другим треугольникам и могли быть объединены в грани пятиугольника.

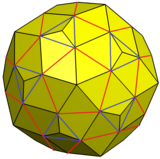Курносый додекаэдр с увеличенными пирамидами и слитыми гранями	Пример варианта	Сеть

Ортогональные проекции [ править ]

Пятиугольный шестиконтаэдр имеет три положения симметрии: два в вершинах и одно в середине.

Ортогональные проекции
Проективный симметрия	[3]	[5] ⁺	[2]
Изображение
Двойной изображение

Связанные многогранники и мозаики [ править ]

Семейство однородных икосаэдрических многогранников.
Symmetry: [5,3], (*532)							[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Этот многогранник топологически связан как часть последовательности многогранников и замощений пятиугольников с конфигурациями граней (V3.3.3.3.n ) . (Последовательность переходит в мозаику гиперболической плоскости до любого n .) Эти гране-транзитивные фигуры обладают (n32) вращательной симметрией .

n 32 мутации симметрии курносых мозаик: 3.3.3.3.n v т и
Symmetry n32	Spherical				Euclidean	Compact hyperbolic		Paracomp.
Symmetry n32	232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

См. также [ править ]

Ссылки [ править ]

^ Коджа, Мехмет; Оздеш Коджа, Назифе; Коч, Рамазон (2010). «Каталонские твердые тела, полученные из трехмерных корневых систем и кватернионов». Журнал математической физики . 51 (4). arXiv : 0908.3272 . дои : 10.1063/1.3356985 . S2CID 115157829 .
^ Ссылка
^ Коджа, Мехмет; Оздеш Коджа, Назифе; Аль-Шуэйлик, Муна (2011). «Киральные многогранники, полученные из диаграмм Кокстера и кватернионов». arXiv : 1006.3149 [ math-ph ].
^ «Пятиугольный шестиконтаэдр — Калькулятор геометрии» . rechneronline.de . Проверено 26 мая 2020 г.

Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371 , ISBN 978-0-521-54325-5 , MR 0730208 (Тринадцать полуправильных выпуклых многогранников и двойственные им многогранники, стр. 29, Пятиугольный шестиконтаэдр)
Симметрии вещей 2008, Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , ISBN 978-1-56881-220-5 [1] (Глава 21, Названия архимедовых и каталонских многогранников и мозаик, страница 287, пятиугольный шестиконтаэдр)