Окружность

В геометрии или описанная окружность описанная — это окружность треугольника окружность , проходящая через все три вершины . Центр этой окружности называется центром описанной окружности треугольника, а его радиус называется радиусом описанной окружности . Центр описанной окружности — это точка пересечения трех серединных перпендикуляров сторон треугольника и центр треугольника .

В более общем смысле, $n$ -сторонний многоугольник со всеми вершинами на одной и той же окружности, также называемый описанной окружностью, называется циклическим многоугольником или, в частном случае $n = 4$ , циклическим четырехугольником . Все прямоугольники , равнобедренные трапеции , прямые воздушные змеи и правильные многоугольники являются циклическими, но не каждый многоугольник.

Конструкция линейки и циркуля [ править ]

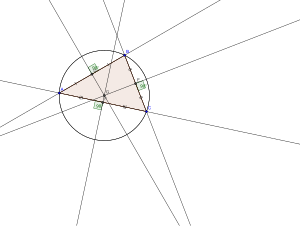
Центр описанной окружности треугольника можно построить , проведя любые два из трех серединных перпендикуляров . Для трех неколлинеарных точек эти две прямые не могут быть параллельны, а центром описанной окружности является точка, в которой они пересекаются. Любая точка биссектрисы равноудалена от двух точек, которые она делит пополам, откуда следует, что эта точка на обеих биссектрисах равноудалена от всех трех вершин треугольника. Радиус описанной окружности — это расстояние от нее до любой из трех вершин.

Альтернативное строительство [ править ]

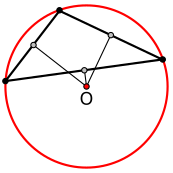
Альтернативный метод определения центра описанной окружности состоит в том, чтобы провести любые две линии, каждая из которых отходит от одной из вершин под углом к общей стороне, при этом общий угол отклонения равен 90° минус угол противоположной вершины. (В случае, если противоположный угол тупой, проведение линии под отрицательным углом означает выход за пределы треугольника.)

В прибрежной навигации описанная окружность треугольника иногда используется как способ получения линии положения с помощью секстанта , когда компас недоступен. Горизонтальный угол между двумя ориентирами определяет описанную окружность, на которой находится наблюдатель.

Уравнения окружности [ править ]

Декартовы координаты [ править ]

В евклидовой плоскости можно явно дать уравнение описанной окружности через декартовы координаты вершин вписанного треугольника. Предположим, что

{\begin{aligned}\mathbf {A} &=(A_{x},A_{y})\\\mathbf {B} &=(B_{x},B_{y})\\\mathbf {C} &=(C_{x},C_{y})\end{aligned}}

– координаты точек $A, B, C$ . Тогда описанная окружность является геометрическим местом точек $\mathbf {v} =(v_{x},v_{y})$ в декартовой плоскости, удовлетворяющей уравнениям

{\begin{aligned}|\mathbf {v} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {A} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {B} -\mathbf {u} |^{2}&=r^{2}\\|\mathbf {C} -\mathbf {u} |^{2}&=r^{2}\end{aligned}}

гарантируя, что точки $A, B, C, v$ находятся на одинаковом расстоянии $r$ от общего центра $\mathbf {u}$ круга. Используя поляризационное тождество , эти уравнения сводятся к условию, что матрица

{\begin{bmatrix}|\mathbf {v} |^{2}&-2v_{x}&-2v_{y}&-1\\|\mathbf {A} |^{2}&-2A_{x}&-2A_{y}&-1\\|\mathbf {B} |^{2}&-2B_{x}&-2B_{y}&-1\\|\mathbf {C} |^{2}&-2C_{x}&-2C_{y}&-1\end{bmatrix}}

имеет ненулевое ядро . Таким образом, описанную окружность можно альтернативно описать как место нулей определителя этой матрицы:

\det {\begin{bmatrix}|\mathbf {v} |^{2}&v_{x}&v_{y}&1\\|\mathbf {A} |^{2}&A_{x}&A_{y}&1\\|\mathbf {B} |^{2}&B_{x}&B_{y}&1\\|\mathbf {C} |^{2}&C_{x}&C_{y}&1\end{bmatrix}}=0.

Используя кофакторное разложение , пусть

{\begin{aligned}S_{x}&={\frac {1}{2}}\det {\begin{bmatrix}|\mathbf {A} |^{2}&A_{y}&1\\|\mathbf {B} |^{2}&B_{y}&1\\|\mathbf {C} |^{2}&C_{y}&1\end{bmatrix}},\\[5pt]S_{y}&={\frac {1}{2}}\det {\begin{bmatrix}A_{x}&|\mathbf {A} |^{2}&1\\B_{x}&|\mathbf {B} |^{2}&1\\C_{x}&|\mathbf {C} |^{2}&1\end{bmatrix}},\\[5pt]a&=\det {\begin{bmatrix}A_{x}&A_{y}&1\\B_{x}&B_{y}&1\\C_{x}&C_{y}&1\end{bmatrix}},\\[5pt]b&=\det {\begin{bmatrix}A_{x}&A_{y}&|\mathbf {A} |^{2}\\B_{x}&B_{y}&|\mathbf {B} |^{2}\\C_{x}&C_{y}&|\mathbf {C} |^{2}\end{bmatrix}}\end{aligned}}

тогда у нас есть $a|\mathbf {v} |^{2}-2\mathbf {Sv} -b=0$ где $\mathbf {S} =(S_{x},S_{y}),$ и – предполагая, что три точки не были на одной линии (в противном случае описанная окружность – это та линия, которую также можно рассматривать как обобщенный круг с $S$ в бесконечности) – $\left|\mathbf {v} -{\tfrac {\mathbf {S} }{a}}\right|^{2}={\tfrac {b}{a}}+{\tfrac {|\mathbf {S} |^{2}}{a^{2}}},$ давая центр описанной окружности ${\tfrac {\mathbf {S} }{a}}$ и радиус описанной окружности ${\sqrt {{\tfrac {b}{a}}+{\tfrac {|\mathbf {S} |^{2}}{a^{2}}}}}.$ Подобный подход позволяет вывести уравнение сферы тетраэдра описанной .

Параметрическое уравнение [ править ]

Единичный вектор, перпендикулярный плоскости, содержащей окружность, определяется выражением

{\widehat {n}}={\frac {(P_{2}-P_{1})\times (P_{3}-P_{1})}{|(P_{2}-P_{1})\times (P_{3}-P_{1})|}}.

Следовательно, учитывая радиус $r$ , центр $P c$ , точку на окружности $P 0$ и единичную нормаль к плоскости, содержащей круг, ${\widehat {n}},$ одно параметрическое уравнение окружности, начинающееся из точки $P 0$ и действующее в положительно ориентированном (т. е. правостороннем ) смысле относительно ${\widehat {n}}$ следующее:

\mathrm {R} (s)=\mathrm {P_{c}} +\cos \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)(P_{0}-P_{c})+\sin \left({\frac {\mathrm {s} }{\mathrm {r} }}\right)\left[{\widehat {n}}\times (P_{0}-P_{c})\right].

Трилинейные и барицентрические координаты [ править ]

Уравнение описанной окружности в трилинейных координатах $x : y : z$ имеет вид ^[1] ${\tfrac {a}{x}}+{\tfrac {b}{y}}+{\tfrac {c}{z}}=0.$ Уравнение описанной окружности в барицентрических координатах $x : y : z$ имеет вид ${\tfrac {a^{2}}{x}}+{\tfrac {b^{2}}{y}}+{\tfrac {c^{2}}{z}}=0.$

Изогональное сопряжение описанной окружности - это бесконечная линия, заданная в трилинейных координатах формулой $ax+by+cz=0$ и в барицентрических координатах $x+y+z=0.$

Высшие измерения [ править ]

Кроме того, описанную окружность треугольника, заключенную в трех измерениях, можно найти обобщенным методом. Пусть $A, B, C$ — трёхмерные точки, образующие вершины треугольника. Начнем с транспонирования системы, чтобы поместить $C$ в начало координат:

{\begin{aligned}\mathbf {a} &=\mathbf {A} -\mathbf {C} ,\\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}}

радиус описанной окружности $r$ Тогда равен

r={\frac {\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left\|\mathbf {a} -\mathbf {b} \right\|}{2\left\|\mathbf {a} \times \mathbf {b} \right\|}}={\frac {\left\|\mathbf {a} -\mathbf {b} \right\|}{2\sin \theta }}={\frac {\left\|\mathbf {A} -\mathbf {B} \right\|}{2\sin \theta }},

где $θ$ — внутренний угол между $a$ и $b$ . Центр описанной окружности, $p 0$ , определяется выражением

p_{0}={\frac {(\left\|\mathbf {a} \right\|^{2}\mathbf {b} -\left\|\mathbf {b} \right\|^{2}\mathbf {a} )\times (\mathbf {a} \times \mathbf {b} )}{2\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}}}+\mathbf {C} .

Эта формула работает только в трех измерениях, поскольку векторное произведение не определено в других измерениях, но ее можно обобщить на другие измерения, заменив векторные произведения следующими тождествами:

{\begin{aligned}\mathbf {u} \times (\mathbf {v} \times \mathbf {w} )&=(\mathbf {u} \cdot \mathbf {w} )\mathbf {v} -(\mathbf {u} \cdot \mathbf {v} )\mathbf {w} ,\\\left\|\mathbf {u} \times \mathbf {v} \right\|^{2}&=\left\|\mathbf {u} \right\|^{2}\left\|\mathbf {v} \right\|^{2}-(\mathbf {u} \cdot \mathbf {v} )^{2}.\end{aligned}}

Это дает нам следующее уравнение для радиуса описанной окружности $r$ :

r={\frac {\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\left\|\mathbf {a} -\mathbf {b} \right\|}{2{\sqrt {\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}}}}}

и следующее уравнение для центра окружности $p 0$ :

p_{0}={\frac {((\left\|\mathbf {a} \right\|^{2}\mathbf {b} -\left\|\mathbf {b} \right\|^{2}\mathbf {a} )\cdot \mathbf {b} )\mathbf {a} -((\left\|\mathbf {a} \right\|^{2}\mathbf {b} -\left\|\mathbf {b} \right\|^{2}\mathbf {a} )\cdot \mathbf {b} )\mathbf {a} }{2(\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2})}}+\mathbf {C}

который можно упростить до:

p_{0}={\frac {\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}(\mathbf {a} +\mathbf {b} )-(\mathbf {a} \cdot \mathbf {b} )(\left\|\mathbf {a} \right\|^{2}\mathbf {b} +\left\|\mathbf {b} \right\|^{2}\mathbf {a} )}{2(\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2})}}+\mathbf {C}

Координаты центра окружности [ править ]

Декартовы координаты [ править ]

Декартовы координаты центра описанной окружности $U=\left(U_{x},U_{y}\right)$ являются

{\begin{aligned}U_{x}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(B_{y}-C_{y})+(B_{x}^{2}+B_{y}^{2})(C_{y}-A_{y})+(C_{x}^{2}+C_{y}^{2})(A_{y}-B_{y})\right]\\[5pt]U_{y}&={\frac {1}{D}}\left[(A_{x}^{2}+A_{y}^{2})(C_{x}-B_{x})+(B_{x}^{2}+B_{y}^{2})(A_{x}-C_{x})+(C_{x}^{2}+C_{y}^{2})(B_{x}-A_{x})\right]\end{aligned}}

с

D=2\left[A_{x}(B_{y}-C_{y})+B_{x}(C_{y}-A_{y})+C_{x}(A_{y}-B_{y})\right].\,

Без ограничения общности это можно выразить в упрощенной форме после перевода вершины $А$ в начало декартовых систем координат, т. е. когда $A'=A-A=(A'_{x},A'_{y})=(0,0).$ В этом случае координаты вершин $B'=B-A$ и $C'=C-A$ представляют векторы из вершины $A'$ в эти вершины. Заметьте, что этот тривиальный перевод возможен для всех треугольников и центра описанной окружности. $U'=(U'_{x},U'_{y})$ треугольника $△ A'B'C'$ следовать как

{\begin{aligned}U'_{x}&={\frac {1}{D'}}\left[C'_{y}({B'_{x}}^{2}+{B'_{y}}^{2})-B'_{y}({C'_{x}}^{2}+{C'_{y}}^{2})\right],\\[5pt]U'_{y}&={\frac {1}{D'}}\left[B'_{x}({C'_{x}}^{2}+{C'_{y}}^{2})-C'_{x}({B'_{x}}^{2}+{B'_{y}}^{2})\right]\end{aligned}}

с

D'=2(B'_{x}C'_{y}-B'_{y}C'_{x}).\,

Благодаря переносу вершины $A$ в начало координат радиус описанной окружности $r$ можно вычислить как

r=\|U'\|={\sqrt {{U'_{x}}^{2}+{U'_{y}}^{2}}}

а фактический центр окружности $△ ABC$ выглядит следующим образом:

U=U'+A

Трилинейные координаты [ править ]

Центр описанной окружности имеет трилинейные координаты. ^[2]

\cos \alpha :\cos \beta :\cos \gamma

где $α, β, γ$ — углы треугольника.

С точки зрения длин сторон $a, b, c$ трилинейные имеют вид ^[3]

a\left(b^{2}+c^{2}-a^{2}\right):b\left(c^{2}+a^{2}-b^{2}\right):c\left(a^{2}+b^{2}-c^{2}\right).

Барицентрические координаты [ править ]

Центр описанной окружности имеет барицентрические координаты. ^[4]

a^{2}\left(b^{2}+c^{2}-a^{2}\right):\;b^{2}\left(c^{2}+a^{2}-b^{2}\right):\;c^{2}\left(a^{2}+b^{2}-c^{2}\right),\,

где $a, b, c$ — длины ребер $BC, CA, AB$ соответственно) треугольника.

В терминах углов треугольника $α, β, γ$ барицентрические координаты центра описанной окружности равны ^[3]

\sin 2\alpha :\sin 2\beta :\sin 2\gamma .

Вектор описанной окружности [ править ]

Поскольку декартовы координаты любой точки представляют собой средневзвешенное значение координат вершин, а веса представляют собой барицентрические координаты точки, нормированные на сумму, равную единице, вектор центра описанной окружности можно записать как

U={\frac {a^{2}\left(b^{2}+c^{2}-a^{2}\right)A+b^{2}\left(c^{2}+a^{2}-b^{2}\right)B+c^{2}\left(a^{2}+b^{2}-c^{2}\right)C}{a^{2}\left(b^{2}+c^{2}-a^{2}\right)+b^{2}\left(c^{2}+a^{2}-b^{2}\right)+c^{2}\left(a^{2}+b^{2}-c^{2}\right)}}.

Здесь $U$ — вектор центра описанной окружности, а $A, B, C$ — векторы вершин. Делитель здесь равен $16 S. 2$ где $S$ — площадь треугольника. Как говорилось ранее

{\begin{aligned}\mathbf {a} &=\mathbf {A} -\mathbf {C} ,\\\mathbf {b} &=\mathbf {B} -\mathbf {C} .\end{aligned}}

скалярных произведений Декартовы координаты из перекрестных и

В евклидовом пространстве неколлинеарные точки $P1 существует единственная окружность ,, P2 проходящая через, P3 любые три$ . Используя декартовы координаты для представления этих точек в виде пространственных векторов , можно использовать скалярное произведение и векторное произведение для расчета радиуса и центра круга. Позволять

\mathrm {P_{1}} ={\begin{bmatrix}x_{1}\\y_{1}\\z_{1}\end{bmatrix}},\mathrm {P_{2}} ={\begin{bmatrix}x_{2}\\y_{2}\\z_{2}\end{bmatrix}},\mathrm {P_{3}} ={\begin{bmatrix}x_{3}\\y_{3}\\z_{3}\end{bmatrix}}

Тогда радиус круга определяется выражением

\mathrm {r} ={\frac {\left|P_{1}-P_{2}\right|\left|P_{2}-P_{3}\right|\left|P_{3}-P_{1}\right|}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|}}

Центр круга задается линейной комбинацией

\mathrm {P_{c}} =\alpha \,P_{1}+\beta \,P_{2}+\gamma \,P_{3}

где

{\begin{aligned}\alpha ={\frac {\left|P_{2}-P_{3}\right|^{2}\left(P_{1}-P_{2}\right)\cdot \left(P_{1}-P_{3}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\\\beta ={\frac {\left|P_{1}-P_{3}\right|^{2}\left(P_{2}-P_{1}\right)\cdot \left(P_{2}-P_{3}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\\\gamma ={\frac {\left|P_{1}-P_{2}\right|^{2}\left(P_{3}-P_{1}\right)\cdot \left(P_{3}-P_{2}\right)}{2\left|\left(P_{1}-P_{2}\right)\times \left(P_{2}-P_{3}\right)\right|^{2}}}\end{aligned}}

Расположение относительно треугольника [ править ]

Положение центра описанной окружности зависит от типа треугольника:

Для остроугольного треугольника (все углы меньше прямого) центр описанной окружности всегда лежит внутри треугольника.
В прямоугольном треугольнике центр описанной окружности всегда лежит в середине гипотенузы . Это одна из форм теоремы Фалеса .
Для тупоугольного треугольника (треугольника, у которого один угол больше прямого) центр описанной окружности всегда лежит вне треугольника.

Центр описанной окружности остроугольного треугольника находится внутри треугольника

Центр описанной окружности прямоугольного треугольника находится в середине гипотенузы

Центр описанной окружности тупоугольного треугольника находится вне треугольника

Эти особенности местоположения можно увидеть, рассмотрев приведенные выше трилинейные или барицентрические координаты центра описанной окружности: все три координаты положительны для любой внутренней точки, по крайней мере одна координата отрицательна для любой внешней точки, одна координата равна нулю и две положительны для невершинная точка на стороне треугольника.

Углы [ править ]

Углы, которые описанная окружность образует со сторонами треугольника, совпадают с углами встречи сторон. Сторона, противолежащая углу $α,$ пересекает окружность дважды: по одному разу на каждом конце; в каждом случае под углом $α$ (аналогично для двух других углов). Это связано с теоремой о альтернативном сегменте , которая гласит, что угол между касательной и хордой равен углу в альтернативном сегменте.

Центр треугольника лежит на описанной окружности [ править ]

В этом разделе углы при вершинах обозначены $A, B, C$ , а все координаты являются трилинейными :

Точка Штейнера : невершинная точка пересечения описанной окружности с эллипсом Штейнера.

{\frac {bc}{b^{2}-c^{2}}}:{\frac {ca}{c^{2}-a^{2}}}:{\frac {ab}{a^{2}-b^{2}}}

( Эллипс Штейнера с центром = центроид (

ABC

) — это эллипс наименьшей площади, который проходит через

A, B, C.

Уравнение для этого эллипса:

{\tfrac {1}{ax}}+{\tfrac {1}{by}}+{\tfrac {1}{cz}}=0

.)

Точка Тарри : антипод точки Штейнера.

\sec(A+\omega ):\sec(B+\omega ):\sec(C+\omega )

Фокус параболы Киперта :

\csc(B-C):\csc(C-A):\csc(A-B).

Другая недвижимость [ править ]

Диаметр окружности описанной окружности, называемый диаметром описанной и равный удвоенному радиусу описанной окружности , можно вычислить как длину любой стороны треугольника, деленную на синус противоположного угла :

{\text{diameter}}={\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}.

Вследствие закона синусов не имеет значения, какая сторона и противолежащий угол взяты: результат будет одинаковым.

Диаметр описанной окружности также можно выразить как

{\begin{aligned}{\text{diameter}}&{}={\frac {abc}{2\cdot {\text{area}}}}={\frac {|AB||BC||CA|}{2|\Delta ABC|}}\\[5pt]&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\[5pt]&{}={\frac {2abc}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}\end{aligned}}

где $a, b, c$ — длины сторон треугольника, а $s={\tfrac {a+b+c}{2}}$ это полупериметр. Выражение $\scriptstyle {\sqrt {s(s-a)(s-b)(s-c)}}$ выше указана площадь треугольника по формуле Герона . ^[5] Тригонометрические выражения для диаметра описанной окружности включают: ^[6]

{\text{diameter}}={\sqrt {\frac {2\cdot {\text{area}}}{\sin A\sin B\sin C}}}.

треугольника Окружность из девяти точек имеет половину диаметра описанной окружности.

В любом треугольнике центр описанной окружности всегда коллинеарен центроиду и ортоцентру . Линия, проходящая через все из них, называется линией Эйлера .

Изогональное сопряжение центра описанной окружности является ортоцентром .

Полезная минимальная ограничивающая окружность из трех точек определяется либо описанной окружностью (где три точки находятся на минимальной ограничивающей окружности), либо двумя точками самой длинной стороны треугольника (где две точки определяют диаметр окружности). Часто путают минимальный ограничивающий круг с описанной окружностью.

Описанная окружность трех коллинеарных точек — это линия, на которой лежат три точки, часто называемая окружностью бесконечного радиуса . Почти коллинеарные точки часто приводят к численной нестабильности при вычислении описанной окружности.

Окружности треугольников тесно связаны с триангуляцией Делоне набора точек .

По теореме Эйлера в геометрии расстояние между центром описанной окружности $O$ и центром $I$ равно

{\overline {OI}}={\sqrt {R(R-2r)}},

где $r$ — радиус вписанной окружности, а $R$ — радиус описанной окружности; следовательно, радиус описанной окружности как минимум в два раза больше внутреннего радиуса ( неравенство треугольника Эйлера ), с равенством только в равностороннем случае. ^[7]^[8]

Расстояние между $O$ и ортоцентром $H$ равно ^[9]^[10]

{\overline {OH}}={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}.

Для центроида $G$ и девятиточечного центра $N$ имеем

{\begin{aligned}{\overline {IG}}&<{\overline {IO}},\\2{\overline {IN}}&<{\overline {IO}},\\{\overline {OI}}^{2}&=2R\cdot {\overline {IN}}.\end{aligned}}

Произведение радиуса вписанной окружности и радиуса описанной окружности треугольника со сторонами $a, b, c$ равно ^[11]

rR={\frac {abc}{2(a+b+c)}}.

С радиусом описанной окружности $R$ , сторонами $a, b, c$ и медианами $m a, m b, m c$ мы имеем ^[12]

{\begin{aligned}3{\sqrt {3}}R&\geq a+b+c\\[5pt]9R^{2}&\geq a^{2}+b^{2}+c^{2}\\[5pt]{\frac {27}{4}}R^{2}&\geq m_{a}^{2}+m_{b}^{2}+m_{c}^{2}.\end{aligned}}

Если медиана $m$ , высота $h$ и внутренняя биссектриса $t$ исходят из одной и той же вершины треугольника с радиусом описанной окружности $R$ , то ^[13]

4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).

Теорема Карно утверждает, что сумма расстояний от центра описанной окружности до трех сторон равна сумме радиуса описанной окружности и внутреннего радиуса . ^[14] Здесь длина отрезка считается отрицательной тогда и только тогда, когда отрезок полностью лежит вне треугольника.

Если в треугольнике есть две отдельные окружности в качестве описанной и вписанной окружности , то существует бесконечное количество других треугольников с той же самой описанной и вписанной окружностью, причем любая точка описанной окружности является вершиной. (Это $n = 3$ случай поризма Понселе при ). Необходимым и достаточным условием существования таких треугольников является указанное выше равенство ${\overline {OI}}={\sqrt {R(R-2r)}}.$ ^[15]

Циклические многоугольники [ править ]

Совокупность точек, лежащих на одной окружности, называется конциклической , а многоугольник, вершины которого лежат на одной окружности, — циклическим многоугольником . Каждый треугольник является вписанным, но многоугольники с числом сторон более трех, как правило, таковыми не являются.

Циклические многоугольники, особенно четырехсторонние циклические четырехугольники , обладают различными особыми свойствами. В частности, противоположные углы вписанного четырёхугольника являются дополнительными углами (в сумме они составляют 180° или π радиан).

См. также [ править ]

Ссылки [ править ]

^ Уитворт, Уильям Аллен (1866). Трилинейные координаты и другие методы современной аналитической геометрии двух измерений . Дейтон, Белл и Ко. с. 199 .
^ Уитворт (1866) , с. 19 .
^ Перейти обратно: ^а ^б Кимберлинг, Кларк. «Часть I: Введение и центры X(1) – X(1000)» . Энциклопедия центров треугольников . Центр описанной окружности указан в разделе X(3).
^ Вайсштейн, Эрик В. «Барицентрические координаты» . Математический мир .
^ Коксетер, HSM (1969). "Глава 1". Введение в геометрию . Уайли. стр. 12–13 . ISBN 0-471-50458-0 .
^ Дорри, Генрих (1965). 100 великих задач элементарной математики . Дувр. п. 379.
^ Нельсон, Роджер, «Неравенство треугольника Эйлера посредством доказательства без слов», Mathematics Magazine 81 (1), февраль 2008 г., 58-61.
^ Свртан, Драгутин; Вельян, Дарко (2012). «Неевклидовы версии некоторых классических неравенств треугольника» . Форум Геометрикорум . 12 : 197–209. См., в частности, стр. 198.
^ Гра, Мари-Николь (2014). «Расстояния между центром описанной окружности касательного треугольника и классическими центрами» . Форум Геометрикорум . 14 : 51–61.
^ Смит, GC; Леверша, Джерри (ноябрь 2007 г.). «Эйлер и геометрия треугольника». Математический вестник . 91 (522): 436–452. дои : 10.1017/S0025557200182087 . JSTOR 40378417 . S2CID 125341434 . См., в частности, стр. 449.
^ Джонсон, Роджер А. (1929). Современная геометрия: элементарный трактат о геометрии треугольника и круга . Houghton Mifflin Co. p. 189, № 298(д). hdl : 2027/wu.89043163211 . Переиздано Dover Publications под названием Advanced Euclidean Geometry , 1960 и 2007 гг.
^ Посаментье, Альфред С.; Леманн, Ингмар (2012). Тайны треугольников . Книги Прометея. стр. 289–290.
^ Альтшиллер Корт, Натан (1952). Геометрия колледжа: введение в современную геометрию треугольника и круга (2-е изд.). Барнс и Ноубл. п. 122, №96. Перепечатано Dover Publications, 2007 г.
^ Суд Альтшиллера (1952) , с. 83.
^ Джонсон (1929) , с. 188.

Внешние ссылки [ править ]

Вывод формулы радиуса описанной окружности треугольника на Mathalino.com
Полуправильные углы и боковые прямоугольники: соответствующие обобщения прямоугольников и ромбов в «Эскизах динамической геометрии» , интерактивном эскизе динамической геометрии.
Вайсштейн, Эрик В. «Описанная окружность» , «Циклический многоугольник» . Математический мир .
описанной окружности треугольника Описанная окружность и центр С интерактивной анимацией
Интерактивный Java-апплет для центра окружности

[WW-1] Уитворт, Уильям Аллен (1866). Трилинейные координаты и другие методы современной аналитической геометрии двух измерений . Дейтон, Белл и Ко. с. 199 .

[FOOTNOTEWhitworth1866[httpsarchiveorgdetailstrilinearcoordin00whituoftpagen61mode2up_p._19]-2] Уитворт (1866) , с. 19 .

[ck-3] Перейти обратно: ^а ^б Кимберлинг, Кларк. «Часть I: Введение и центры X(1) – X(1000)» . Энциклопедия центров треугольников . Центр описанной окружности указан в разделе X(3).

[4] Вайсштейн, Эрик В. «Барицентрические координаты» . Математический мир .

[5] Коксетер, HSM (1969). "Глава 1". Введение в геометрию . Уайли. стр. 12–13 . ISBN 0-471-50458-0 .

[6] Дорри, Генрих (1965). 100 великих задач элементарной математики . Дувр. п. 379.

[Nelson-7] Нельсон, Роджер, «Неравенство треугольника Эйлера посредством доказательства без слов», Mathematics Magazine 81 (1), февраль 2008 г., 58-61.

[8] Свртан, Драгутин; Вельян, Дарко (2012). «Неевклидовы версии некоторых классических неравенств треугольника» . Форум Геометрикорум . 12 : 197–209. См., в частности, стр. 198.

[9] Гра, Мари-Николь (2014). «Расстояния между центром описанной окружности касательного треугольника и классическими центрами» . Форум Геометрикорум . 14 : 51–61.

[10] Смит, GC; Леверша, Джерри (ноябрь 2007 г.). «Эйлер и геометрия треугольника». Математический вестник . 91 (522): 436–452. дои : 10.1017/S0025557200182087 . JSTOR 40378417 . S2CID 125341434 . См., в частности, стр. 449.

[11] Джонсон, Роджер А. (1929). Современная геометрия: элементарный трактат о геометрии треугольника и круга . Houghton Mifflin Co. p. 189, № 298(д). hdl : 2027/wu.89043163211 . Переиздано Dover Publications под названием Advanced Euclidean Geometry , 1960 и 2007 гг.

[12] Посаментье, Альфред С.; Леманн, Ингмар (2012). Тайны треугольников . Книги Прометея. стр. 289–290.

[13] Альтшиллер Корт, Натан (1952). Геометрия колледжа: введение в современную геометрию треугольника и круга (2-е изд.). Барнс и Ноубл. п. 122, №96. Перепечатано Dover Publications, 2007 г.

[FOOTNOTEAltshiller_Court195283-14] Суд Альтшиллера (1952) , с. 83.

[FOOTNOTEJohnson1929188-15] Джонсон (1929) , с. 188.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]