центроид

Центроид треугольника

В математике и физике центроид представляет , также известный как геометрический центр или центр фигуры , плоской фигуры или объемной фигуры, собой среднее арифметическое положение всех точек на поверхности фигуры. То же определение распространяется на любой объект в $n$-мерное евклидово пространство .

В геометрии часто предполагается равномерная плотность массы , и в этом случае барицентр или центр масс совпадает с центроидом. Неформально это можно понимать как точку, в которой вырез определенной формы (с равномерно распределенной массой) может быть идеально сбалансирован на кончике булавки.

изменения силы тяжести В физике, если учитывать , то центр тяжести можно определить как средневзвешенное значение всех точек, взвешенных по их удельному весу .

В географии центр тяжести радиальной проекции области земной поверхности на уровень моря является географическим центром региона .

История

Термин «центроид» появился в чеканке недавнего времени (1814 г.). Он используется вместо старых терминов «центр тяжести» и « центр масс », когда необходимо подчеркнуть чисто геометрические аспекты этой точки. Этот термин свойственен английскому языку; Во французском языке, например, в большинстве случаев используется « центр тяжести », а в других языках используются термины аналогичного значения.

Центр тяжести, как следует из названия, — понятие, возникшее в механике, скорее всего, в связи со строительной деятельностью. Неизвестно, когда эта идея впервые появилась, поскольку концепция, вероятно, приходила в голову многим людям индивидуально с небольшими различиями. Тем не менее, центр тяжести фигур широко изучался в древности; Боссут приписывает Архимеду (287–212 гг. До н.э.) то, что он был первым, кто нашел центр тяжести плоских фигур, хотя он никогда не давал ему определения. Трактовка Архимедом центроидов твердых тел утеряна.

Маловероятно, что Архимед узнал теорему о том, что медианы треугольника встречаются в точке — центре тяжести треугольника, — непосредственно от Евклида , поскольку этого утверждения нет в «Началах» . Первое явное утверждение этого предложения принадлежит Герону Александрийскому (вероятно, первый век нашей эры) и встречается в его «Механике» . Можно попутно добавить, что это положение не стало обычным явлением в учебниках по плоской геометрии вплоть до XIX века.

Свойства

Геометрический центр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь центр тяжести, находящийся за пределами самой фигуры. Например, центр тяжести кольца или чаши находится в центральной пустоте объекта.

Если центроид определен, он является фиксированной точкой всех изометрий в своей группе симметрии . В частности, геометрический центр тяжести объекта лежит в пересечении всех гиперплоскостей симметрии его . Центр тяжести многих фигур ( правильный многоугольник , правильный многогранник , цилиндр , прямоугольник , ромб , круг , сфера , эллипс , эллипсоид , суперэллипс , суперэллипсоид и т. д.) можно определить только по этому принципу.

В частности, центр тяжести параллелограмма — это точка встречи двух его диагоналей . Это не относится к другим четырехугольникам .

По той же причине центроид объекта с трансляционной симметрией не определен (или лежит вне окружающего пространства), поскольку сдвиг не имеет фиксированной точки.

Примеры

Центр тяжести треугольника — это пересечение трех медиан треугольника (каждая медиана соединяет вершину с серединой противоположной стороны).

Другие свойства центроида треугольника см. ниже .

Определение

Смотрите также: Центр масс § Определение

Метод отвеса

Центр тяжести плоской пластинки с однородной плотностью , такой как на рисунке (а) ниже, можно определить экспериментально, используя отвес и булавку, чтобы найти совмещенный центр массы тонкого тела однородной плотности, имеющего ту же форму. Тело удерживается штифтом, вставленным в точку вне предполагаемого центроида таким образом, что оно может свободно вращаться вокруг штифта; затем отвес снимают со штифта (рис. b). Положение отвеса отслеживается на поверхности, и процедура повторяется, вставляя штифт в любую другую точку (или несколько точек) от центроида объекта. Единственной точкой пересечения этих линий будет центроид (рисунок в). При условии, что тело имеет одинаковую плотность, все построенные таким образом линии будут включать в себя центр тяжести и все линии будут пересекаться точно в одном и том же месте.

(а)	(б)	(с)

Этот метод можно распространить (теоретически) на вогнутые формы, где центр тяжести может лежать вне формы, и практически на твердые тела (опять же, с одинаковой плотностью), где центр тяжести может лежать внутри тела. (Виртуальные) положения отвесов необходимо записывать другими способами, а не путем их рисования вдоль формы.

Метод балансировки

Для выпуклых двумерных фигур центр тяжести можно найти, сбалансировав фигуру по меньшей фигуре, например вершине узкого цилиндра. Центр тяжести находится где-то в пределах контакта между двумя фигурами (и точно в той точке, где фигура будет балансировать на штифте). В принципе, для нахождения центроида с произвольной точностью можно использовать постепенно сужающиеся цилиндры. На практике воздушные потоки делают это невозможным. Однако, отмечая диапазон перекрытия нескольких весов, можно добиться значительного уровня точности.

Из конечного набора точек

Центр тяжести конечного множества $k$ точки $\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{k}$ в $\mathbb {R} ^{n}$ является

$$\mathbf {C} ={\frac {\mathbf {x} _{1}+\mathbf {x} _{2}+\cdots +\mathbf {x} _{k}}{k}}.$$

Эта точка минимизирует сумму квадратов евклидовых расстояний между собой и каждой точкой набора.

Путем геометрической декомпозиции

Центр тяжести плоской фигуры $X$ можно вычислить, разделив его на конечное число более простых фигур. $X_{1},X_{2},\dots ,X_{n},$ вычисление центроида $C_{i}$ и площадь $A_{i}$ каждой части, а затем вычисляем

$$C_{x}={\frac {\sum _{i}{C_{i}}_{x}A_{i}}{\sum _{i}A_{i}}},\quad C_{y}={\frac {\sum _{i}{C_{i}}_{y}A_{i}}{\sum _{i}A_{i}}}.$$

Дырки на фигуре $X,$ перекрытия между частями или части, выходящие за пределы фигуры, можно обрабатывать с помощью отрицательных областей. $A_{i}.$ А именно, меры $A_{i}$ следует брать с положительными и отрицательными знаками таким образом, чтобы сумма знаков $A_{i}$ для всех частей, охватывающих данную точку $p$ является $1$ если $p$ принадлежит $X,$ и $0$ в противном случае.

Например, фигуру ниже (а) легко разделить на квадрат и треугольник, оба с положительной площадью; и круглое отверстие с отрицательной площадью (b).

(а) 2D-объект

(б) Объект, описанный с использованием более простых элементов

(в) Центроиды элементов объекта

Центр тяжести каждой детали можно найти в любом списке центроидов простых форм (c). Тогда центр тяжести фигуры — это средневзвешенное значение трех точек. Горизонтальное положение центроида от левого края рисунка равно

$$x={\frac {5\times 10^{2}+13.33\times {\frac {1}{2}}10^{2}-3\times \pi 2.5^{2}}{10^{2}+{\frac {1}{2}}10^{2}-\pi 2.5^{2}}}\approx 8.5{\text{ units}}.$$

Вертикальное положение центроида находится таким же образом.

Та же формула справедлива для любых трехмерных объектов, за исключением того, что каждый $A_{i}$ должен быть объём $X_{i},$а не его площадь. Это справедливо также для любого подмножества $\mathbb {R} ^{d},$ для любого размера $d,$ с областями, замененными $d$-размерные меры деталей.

По интегральной формуле

Центр тяжести подмножества $X$ из $\mathbb {R} ^{n}$ также можно вычислить по формуле

$$C={\frac {\int xg(x)\ dx}{\int g(x)\ dx}}$$

где интегралы берутся по всему пространству $\mathbb {R} ^{n},$ и $g$ — характеристическая функция подмножества $X$ из $\mathbb {R} ^{n}\!:\ g(x)=1$ если $x\in X$ и $g(x)=0$ в противном случае. Обратите внимание, что знаменатель — это просто мера множества. $X.$ Эту формулу нельзя применить, если множество $X$ имеет нулевую меру или любой из интегралов расходится.

Другая формула для центроида:

$$C_{k}={\frac {\int zS_{k}(z)\ dz}{\int g(x)\ dx}},$$

где $C_{k}$ это $k$координата $C,$ и $S_{k}(z)$ является мерой пересечения $X$ с гиперплоскостью, определяемой уравнением $x_{k}=z.$ Опять же, знаменатель — это просто мера $X.$

В частности, для плоской фигуры барицентрические координаты имеют вид

$$C_{\mathrm {x} }={\frac {\int xS_{\mathrm {y} }(x)\ dx}{A}},\quad C_{\mathrm {y} }={\frac {\int yS_{\mathrm {x} }(y)\ dy}{A}},$$

где $A$ это площадь фигуры $X,$ $S_{\mathrm {y} }(x)$ это длина пересечения $X$ с вертикальной линией по оси абсцисс $x,$ и $S_{\mathrm {x} }(y)$ это длина пересечения $X$ с горизонтальной линией по ординате $y.$

Из ограниченной области

Центроид $({\bar {x}},\;{\bar {y}})$ области, ограниченной графиками непрерывных функций $f$ и $g$ такой, что $f(x)\geq g(x)$ на интервале $[a,b],$ $a\leq x\leq b$ дан кем-то

$${\begin{aligned}{\bar {x}}&={\frac {1}{A}}\int _{a}^{b}x{\bigl (}f(x)-g(x){\bigr )}\,dx,\\[5mu]{\bar {y}}&={\frac {1}{A}}\int _{a}^{b}{\tfrac {1}{2}}{\bigl (}f(x)+g(x){\bigr )}{\bigl (}f(x)-g(x){\bigr )}\,dx,\end{aligned}}$$

где $A$ - площадь региона (задается ${\textstyle \int _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx}$).

С интегралом

Интеграл ( родственник планиметра ) можно использовать для нахождения центроида объекта неправильной формы с гладкой (или кусочно-гладкой) границей. Используемый математический принцип является частным случаем теоремы Грина .

Г-образного объекта

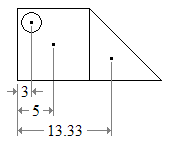
Это метод определения центроида L-образного объекта.

1. Разделите фигуру на два прямоугольника, как показано на рис. 2. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центр тяжести фигуры должен лежать на этой линии. $AB.$
2. Разделите фигуру на два других прямоугольника, как показано на рис. 3. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центр тяжести L-образной формы должен лежать на этой линии. $CD.$
3. Поскольку центр тяжести фигуры должен лежать вдоль $AB$ а также вместе $CD,$ оно должно быть на пересечении этих двух линий, на $O.$ Смысл $O$ может лежать внутри или снаружи L-образного объекта.

Треугольника

Основная статья: Центр треугольника

Центр тяжести треугольника — это точка пересечения его медиан (линий, соединяющих каждую вершину с серединой противоположной стороны). Центроид делит каждую из медиан в соотношении $2:1,$ то есть он расположен ${\tfrac {1}{3}}$ расстояния от каждой стороны до противоположной вершины (см. рисунки справа). Его декартовы координаты являются средними координатами трех вершин. То есть, если три вершины $L=(x_{L},y_{L}),$ $M=(x_{M},y_{M}),$ и $N=(x_{N},y_{N}),$ затем центроид (обозначаемый $C$ здесь, но чаще всего обозначается $G$ в геометрии треугольника )

$$C={\tfrac {1}{3}}(L+M+N)={\bigl (}{\tfrac {1}{3}}(x_{L}+x_{M}+x_{N}),{\tfrac {1}{3}}(y_{L}+y_{M}+y_{N}){\bigr )}.$$

Таким образом, центр тяжести находится в ${\tfrac {1}{3}}:{\tfrac {1}{3}}:{\tfrac {1}{3}}$ в барицентрических координатах .

В трилинейных координатах центр тяжести можно выразить любым из этих эквивалентных способов через длины сторон. $a,b,c$ и углы при вершинах $L,M,N$:

$${\begin{aligned}C&={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ca:ab=\csc L:\csc M:\csc N\\[6pt]&=\cos L+\cos M\cdot \cos N:\cos M+\cos N\cdot \cos L:\cos N+\cos L\cdot \cos M\\[6pt]&=\sec L+\sec M\cdot \sec N:\sec M+\sec N\cdot \sec L:\sec N+\sec L\cdot \sec M.\end{aligned}}$$

Центроид также является физическим центром масс, если треугольник сделан из однородного листа материала; или если вся масса сосредоточена в трех вершинах и равномерно распределена между ними. С другой стороны, если масса распределена по периметру треугольника с равномерной линейной плотностью , то центр массы лежит в центре Шпикера ( инцентре медиального треугольника ), который (вообще) не совпадает с геометрическим центр тяжести полного треугольника.

Площадь треугольника равна ${\tfrac {3}{2}}$ умножить длину любой стороны на расстояние по перпендикуляру от стороны к центру тяжести.

Центр тяжести треугольника лежит на линии Эйлера между его ортоцентром $H$ и его центр окружности $O,$ ровно в два раза ближе к последнему, чем к первому:

$${\overline {CH}}=2{\overline {CO}}.$$

Кроме того, для инцентра $I$ и девятиочковый центр $N,$ у нас есть

$${\begin{aligned}{\overline {CH}}&=4{\overline {CN}},\\[5pt]{\overline {CO}}&=2{\overline {CN}},\\[5pt]{\overline {IC}}&<{\overline {HC}},\\[5pt]{\overline {IH}}&<{\overline {HC}},\\[5pt]{\overline {IC}}&<{\overline {IO}}.\end{aligned}}$$

Если $G$ это центр тяжести треугольника $ABC,$ затем

$$({\text{Area of }}\triangle ABG)=({\text{Area of }}\triangle ACG)=({\text{Area of }}\triangle BCG)={\tfrac {1}{3}}({\text{Area of }}\triangle ABC).$$

Изогонально -сопряженная центроида треугольника является его симмедианой точкой .

Любая из трех медиан, проходящих через центр тяжести, делит площадь треугольника пополам. Это не относится к другим линиям, проходящим через центр тяжести; Наибольшее отклонение от деления равной площади происходит, когда линия, проходящая через центр тяжести, параллельна стороне треугольника, образуя меньший треугольник и трапецию ; в этом случае площадь трапеции равна ${\tfrac {5}{9}}$ как у исходного треугольника.

Позволять $P$ любая точка плоскости треугольника с вершинами $A,B,C$ и центроид $G.$ Тогда сумма квадратов расстояний $P$ из трех вершин превышает сумму квадратов расстояний от центроида $G$ от вершин на трехкратный квадрат расстояния между $P$ и $G$:

$$PA^{2}+PB^{2}+PC^{2}=GA^{2}+GB^{2}+GC^{2}+3PG^{2}.$$

Сумма квадратов сторон треугольника равна трехкратной сумме квадратов расстояний центроида от вершин:

$$AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2}).$$

Центр тяжести треугольника — это точка, которая максимизирует произведение направленных расстояний точки от боковых линий треугольника.

Позволять $ABC$ будет треугольник, пусть $G$ будет его центроидом, и пусть $D,E,F$ быть серединами отрезков $BC,CA,AB,$соответственно. Для любой точки $P$ в плоскости $ABC,$

$$PA+PB+PC\leq 2(PD+PE+PF)+3PG.$$

Многоугольника

Центр тяжести несамопересекающегося замкнутого многоугольника, определенного формулой $n$ вершины $(x_{0},y_{0}),\;$$(x_{1},y_{1}),\;\ldots ,\;$$(x_{n-1},y_{n-1}),$ в этом суть $(C_{x},C_{y}),$ где

$$C_{\mathrm {x} }={\frac {1}{6A}}\sum _{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}),$$

и

$$C_{\mathrm {y} }={\frac {1}{6A}}\sum _{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}),$$

и где $A$ - подписанная площадь многоугольника, как описано в формуле шнурков :

$$A={\frac {1}{2}}\sum _{i=0}^{n-1}(x_{i}\ y_{i+1}-x_{i+1}\ y_{i}).$$

В этих формулах предполагается, что вершины пронумерованы в порядке их появления по периметру многоугольника; кроме того, вершина $(x_{n},y_{n})$ предполагается таким же, как $(x_{0},y_{0}),$ значение $i+1$ в последнем случае необходимо зациклиться на $i=0.$ (Если точки пронумерованы по часовой стрелке, площадь $A,$рассчитанное, как указано выше, будет отрицательным; однако координаты центроида будут правильными даже в этом случае.)

Конуса или пирамиды

Центр тяжести конуса или пирамиды расположен на отрезке, соединяющем вершину с центроидом основания. Для сплошного конуса или пирамиды центр тяжести равен ${\tfrac {1}{4}}$расстояние от основания до вершины. Для конуса или пирамиды, представляющей собой всего лишь оболочку (полую) без основания, центр тяжести равен ${\tfrac {1}{3}}$ расстояние от базовой плоскости до вершины.

О тетраэдре и n -мерном симплексе

Тетраэдр имеющий — это объект в трехмерном пространстве, четыре грани в виде треугольников . Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой , а отрезок, соединяющий середины двух противоположных ребер, — бимедианой . Следовательно, существует четыре медианы и три бимедианы. Все эти семь сегментов линий встречаются в центре тяжести тетраэдра. Медианы делятся на центр тяжести в соотношении $3:1.$Центр тяжести тетраэдра — это середина между его точкой Монжа и центром описанной окружности (центром описанной сферы). Эти три точки определяют линию Эйлера тетраэдра, аналогичную линии Эйлера треугольника.

Эти результаты распространяются на любые $n$-мерный симплекс следующим образом. Если множество вершин симплекса ${v_{0},\ldots ,v_{n}},$ тогда, рассматривая вершины как векторы , центроид равен

$$C={\frac {1}{n+1}}\sum _{i=0}^{n}v_{i}.$$

Геометрический центр тяжести совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как $n+1$ равные массы.

Полушария

Центр тяжести твердого полушария (т.е. половина сплошного шара) делит отрезок, соединяющий центр сферы с полюсом полусферы, в соотношении $3:5$ (т.е. это ложь ${\tfrac {3}{8}}$пути от центра к полюсу). Центр тяжести полой полусферы (т.е. половины полой сферы) делит отрезок линии, соединяющий центр сферы с полюсом полусферы, пополам.

См. также

• Чебышев центр
• Круговое среднее
• Фреше означает
• k -средних алгоритм
• Список центроидов
• Медоид
• Теорема Паппа о центроиде

Ссылки

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: введение в современную геометрию треугольника и круга (2-е изд.), Нью-Йорк: Barnes & Noble , LCCN   52013504
• Бурк, Пол (июль 1997 г.). «Вычисление площади и центроида многоугольника» .
• Джонсон, Роджер А. (2007), Расширенная евклидова геометрия , Дувр
• Кей, Дэвид К. (1969), Геометрия колледжа , Нью-Йорк: Холт, Райнхарт и Уинстон , LCCN   69012075
• Ларсон, Роланд Э.; Хостетлер, Роберт П.; Эдвардс, Брюс Х. (1998), Исчисление одной переменной (6-е изд.), Houghton Mifflin Company
• Проттер, Мюррей Х.; Морри, Чарльз Б. младший (1970), Колледжское исчисление с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли , LCCN   76087042
• Сангвин, CJ, Определение местоположения центра масс механическими средствами (PDF) , заархивировано из оригинала (PDF) 13 ноября 2013 г.

Внешние ссылки

• Вайсштейн, Эрик В. «Геометрический центроид» . Математический мир .
• Энциклопедия центров треугольников Кларка Кимберлинга. Центроид индексируется как X(2).
• Характеристическое свойство центроида при разрезании узла
• Интерактивная анимация, показывающая центроид треугольника и построение центроида с помощью циркуля и линейки.
• Экспериментально найти медианы и центр тяжести треугольника в Dynamic Geometry Sketches , интерактивном эскизе динамической геометрии с использованием гравитационного симулятора Золушки.