Ромб

Ромб
Ромб
	Ромб в двух разных ориентациях
Тип	четырехугольник , трапеция , параллелограмм , воздушный змей
Ребра и вершины	4
Символ Шлефли	{ } + { } ; {2 а }
Диаграммы Кокстера – Динкина
Группа симметрии	Диэдр (D 2 ), [2], (*22), порядок 4
Область	(половина произведения диагоналей)
Характеристики	выпуклый , изотоксальный
Двойной полигон	прямоугольник

В плоской евклидовой геометрии ромб , ( мн.: ромбы или ромбы ) — это четырехугольник все четыре стороны которого имеют одинаковую длину. Другое название — равносторонний четырехугольник , поскольку равносторонний означает, что все его стороны равны по длине. Ромб часто называют « ромбом », по названию бубновой масти в игральных картах , которая напоминает проекцию октаэдрического ромба или ромба , хотя первая иногда относится именно к ромбу с углом 60° (который некоторые авторы называют ромбом). калиссон по французской сладости ^[1]— см. также Полиалмонд ), причем последнее иногда относится именно к ромбу с углом 45°.

Каждый ромб является простым (несамопересекающимся) и является частным случаем параллелограмма и воздушного змея . Ромб с прямыми углами является квадратом . ^[2]

Этимология

Слово «ромб» происходит от древнегреческого : ῥόμβος , латинизированного : rhómbos , что означает нечто вращающееся. ^[3] которое происходит от глагола ῥέμβω , латинизированного: rhémbō , что означает «вращаться и вращаться». ^[4] Это слово использовалось как Евклидом , так и Архимедом , которые использовали термин «сплошной ромб» для биконуса , двух правильных круглых конусов , имеющих общее основание. ^[5]

называем ромбом, Поверхность, которую мы сегодня представляет собой поперечное сечение биконуса на плоскости, проходящей через вершины двух конусов.

Характеристики

Простой он (несамопересекающийся ) четырехугольник является ромбом тогда и только тогда, когда соответствует любому из следующих условий: ^[6]^[7]

параллелограмм , в котором диагональ делит внутренний угол пополам
параллелограмм, у которого хотя бы две последовательные стороны равны по длине
параллелограмм, у которого диагонали перпендикулярны ( ортодиагональный параллелограмм)
четырехугольник с четырьмя сторонами одинаковой длины (по определению)
четырехугольник, в котором диагонали перпендикулярны и делят друг друга пополам
четырехугольник, в котором каждая диагональ делит пополам два противоположных внутренних угла
четырехугольник ABCD , имеющий точку P четыре треугольника ABP , BCP , CDP и DAP в своей плоскости, такую, что все конгруэнтны. ^[8]
четырехугольник ABCD , в котором вписанные окружности в треугольниках ABC , BCD , CDA и DAB имеют общую точку. ^[9]

Основные свойства

Каждый ромб имеет две диагонали , соединяющие пары противоположных вершин, и две пары параллельных сторон. Используя конгруэнтные треугольники , можно доказать , что ромб симметричен относительно каждой из этих диагоналей. Отсюда следует, что любой ромб обладает следующими свойствами:

Противоположные углы ромба имеют одинаковую меру.
Две диагонали ромба перпендикулярны ; то есть ромб — это ортодиагональный четырёхугольник .
Его диагонали делят противоположные углы пополам.

Первое свойство означает, что каждый ромб является параллелограммом . Таким образом, ромб обладает всеми свойствами параллелограмма : например, противоположные стороны параллельны; смежные углы являются дополнительными ; две диагонали делят друг друга пополам; любая линия, проходящая через среднюю точку, делит площадь пополам; а сумма квадратов сторон равна сумме квадратов диагоналей ( закон параллелограмма ). Обозначая таким образом общую сторону a , а диагонали p и q , в каждом ромбе

\displaystyle 4a^{2}=p^{2}+q^{2}.

Не всякий параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является ромбом. Вообще любой четырехугольник с перпендикулярными диагоналями, одна из которых является линией симметрии, является воздушным змеем . Каждый ромб является коршуном, а любой четырехугольник, который является одновременно коршуном и параллелограммом, является ромбом.

Ромб – это касательный четырехугольник . ^[10] То есть вписанная окружность касается всех четырех сторон.

Ромб. Каждый угол, отмеченный черной точкой, является прямым. Высота h — это расстояние по перпендикуляру между любыми двумя несмежными сторонами, равное диаметру вписанной окружности. Диагонали длин p и q представляют собой отрезки красного пунктира.

Диагонали

Длину диагоналей p = AC и q = BD можно выразить через сторону ромба a и один угол при вершине α как

p=a{\sqrt {2+2\cos {\alpha }}}

и

q=a{\sqrt {2-2\cos {\alpha }}}.

Эти формулы являются прямым следствием закона косинусов .

Радиус

Внутренний радиус (радиус окружности, вписанной в ромб), обозначаемый $r$ , можно выразить через диагонали $p$ и $q$ как ^[10]

r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}},

или через длину стороны $a$ и любой угол при вершине $α$ или $β$ как

r={\frac {a\sin \alpha }{2}}={\frac {a\sin \beta }{2}}.

Область

Как и для всех параллелограммов , площадь К ромба равна произведению его основания и высоты ( h ). Основание — это просто любая сторона длиной a :

K=a\cdot h.

Площадь также можно выразить как произведение основания квадрата на синус любого угла:

K=a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta ,

или через высоту и вершины угол :

K={\frac {h^{2}}{\sin \alpha }},

или как половина произведения диагоналей p , q :

K={\frac {p\cdot q}{2}},

или как полупериметр , умноженный на радиус круга , вписанного в ромб (внутренний радиус):

K=2a\cdot r.

Другой способ, как и в случае с параллелограммами, — рассматривать две смежные стороны как векторы, образующие бивектор , поэтому площадь — это величина бивектора (величина векторного произведения двух векторов), которая является определителем двух векторов. Декартовы координаты векторов: K = x ₁ y ₂ – x ₂ y ₁ . ^[11]

Двойные свойства

Двойной многоугольник ромба представляет собой прямоугольник : ^[12]

У ромба все стороны равны, а у прямоугольника все углы равны.
У ромба противоположные углы равны, а у прямоугольника противоположные стороны равны.
В ромб есть вписанная окружность, а в прямоугольник — описанная окружность .
У ромба ось симметрии проходит через каждую пару противоположных при вершинах углов, а у прямоугольника ось симметрии проходит через каждую пару противоположных сторон.
Диагонали ромба пересекаются под равными углами, а диагонали прямоугольника равны.
Фигура, образованная соединением середин сторон ромба, представляет собой прямоугольник , и наоборот.

Декартово уравнение

Стороны ромба с центром в начале координат и диагоналями, падающими на ось, состоят из всех точек ( x, y ), удовлетворяющих

\left|{\frac {x}{a}}\right|\!+\left|{\frac {y}{b}}\right|\!=1.

Вершины находятся в $(\pm a,0)$ и $(0,\pm b).$ Это частный случай суперэллипса с показателем 1.

Другие объекты недвижимости

Одним из пяти типов двумерных решеток является ромбическая решетка, также называемая центрированной прямоугольной решеткой .
Идентичные ромбы можно замостить 2D-плоскость тремя различными способами, в том числе, для ромба с углом 60°, замощением ромба .

Как топологические квадратные мозаики		под углом 30-60 градусов. Ромбическая плитка

Трехмерные аналоги ромба включают бипирамиду и биконус как поверхность вращения .

Как грани многогранника

Выпуклые многогранники с ромбами включают в себя бесконечное множество ромбических зоноэдров , которые можно рассматривать как проективные оболочки гиперкубов .

Ромбоэдр (также называемому прямоугольным параллелепипедом), за исключением того , (также называемый ромбическим шестигранником) — это трехмерная фигура, подобная кубоиду что его 3 пары параллельных граней представляют собой до 3 типов ромбов вместо прямоугольников.
Ромбдодекаэдр , — выпуклый многогранник которого являются 12 равных ромбов гранями .
Ромбический триаконтаэдр представляет собой выпуклый многогранник с 30 золотыми ромбами (ромбы, диагонали которых находятся в золотом сечении ) в качестве граней.
Большой ромбический триаконтаэдр собой невыпуклый равногранный изотоксальный многогранник представляет с 30 пересекающимися ромбическими гранями.
Ромбический гексаконтаэдр представляет собой звездчатую форму ромбодтриаконтаэдра. Он невыпуклый, с 60 золотыми ромбическими гранями икосаэдрической симметрии .
Ромбический эннеаконтаэдр — это многогранник, состоящий из 90 ромбических граней, в каждой вершине которых сходятся три, пять или шесть ромбов. Имеет 60 широких и 30 тонких ромбов.
Ромбический икосаэдр — это многогранник, состоящий из 20 ромбических граней, из которых три, четыре или пять сходятся в каждой вершине. У него 10 граней на полярной оси и 10 граней, следующих за экватором.

Пример многогранников со всеми ромбическими гранями
изоэдрический		Изоэдральный золотой ромб		2-изоэдрический	3-изоэдрический

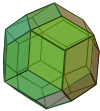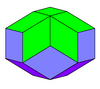Трехугольный трапецоэдр	Ромбический додекаэдр	Ромбический триаконтаэдр	Ромбический икосаэдр	Ромбический эннеаконтаэдр	Ромбоэдр

Смотрите также

Бриллиант Меркель
Ромб Михаэлиса в анатомии человека
Ромбоид — параллелепипед или параллелограмм, не являющийся ни ромбом, ни прямоугольником.
Ромбическая антенна
Ромбические шахматы
Флаг департамента Северный Сантандер Колумбии, содержащий четыре звезды в форме ромба.
Суперэллипс (включает ромб с закругленными углами)

Внешние ссылки

Параллелограмм и Ромб - Анимационный курс (Построение, Окружность, Площадь)
Определение ромба, Открытый справочник по математике с интерактивным апплетом.
Площадь ромба, Открытый справочник по математике — показаны три различных способа вычисления площади ромба с помощью интерактивного апплета.

[1] Альсина, Клауди; Нельсен, Роджер Б. (31 декабря 2015 г.). Математическая космическая одиссея: твердотельная геометрия в XXI веке . Американское математическое соц. ISBN 9781614442165 .

[2] Примечание: исходное определение Евклида и определение ромба в некоторых английских словарях исключают квадраты, но современные математики предпочитают инклюзивное определение. См., например, Де Вильерс, Майкл (февраль 1994 г.). «Роль и функция иерархической классификации четырехугольников». Для изучения математики . 14 (1): 11–18. JSTOR 40248098 .

[3] ῥόμβος. Архивировано 8 ноября 2013 г. в Wayback Machine , Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон , о Персее.

[4] ρέμβω. Архивировано 8 ноября 2013 г. в Wayback Machine , Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон , о Персее.

[5] «Происхождение ромба» . Архивировано из оригинала 02 апреля 2015 г. Проверено 25 января 2005 г.

[6] Залман Усискин и Дженнифер Гриффин, « Классификация четырехугольников. Исследование определения. Архивировано 26 февраля 2020 г. в Wayback Machine », Information Age Publishing, 2008, стр. 55-56.

[7] Оуэн Байер, Феликс Лазебник и Дейдра Смельцер , Методы евклидовой геометрии. Архивировано 1 сентября 2019 г. в Wayback Machine , Математическая ассоциация Америки, 2010, стр. 53.

[8] Пэрис Памфилос (2016), «Характеристика ромба», Forum Geometricorum 16 , стр. 331–336, [1] Архивировано 23 октября 2016 г. в Wayback Machine.

[9] «IMOMath, «26-я Бразильская математическая олимпиада 2004 г.» » (PDF) . Архивировано (PDF) из оригинала 18 октября 2016 г. Проверено 6 января 2020 г.

[Mathworld-10] Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Ромб» . Математический мир .

[11] WildLinAlg, эпизод 4. Архивировано 5 февраля 2017 г. в Wayback Machine , Норман Дж. Вайлдбергер, Univ. Нового Южного Уэльса, 2010 г., лекция на YouTube.

[12] де Вильерс, Майкл, «Равноугольные циклические и равносторонние описанные многоугольники», Mathematical Gazette 95, март 2011 г., 102–107.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]