База (геометрия)

Скелетная пирамида с основанием . выделенным

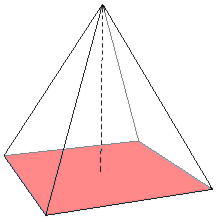
В геометрии основанием перпендикулярно является сторона многоугольника направлению или грань многогранника , в частности, ориентированная измерения высоты или тому, что считается «низом» фигуры. Этот термин обычно применяется в плоской геометрии к треугольникам , параллелограммам , трапециям , а в объемной геометрии к цилиндрам , конусам , пирамидам , параллелепипедам , призмам и усеченным конусам .

Сторону или точку, противоположную основанию, часто называют вершиной или вершиной формы.

Треугольника

Высота в D ( из A пересекает расширенное основание точка вне треугольника).

В треугольнике основанием можно считать любую произвольную сторону . Две конечные точки основания называются базовыми вершинами , а соответствующие углы называются базовыми углами . Третья вершина, противоположная основанию, называется вершиной .

Расширенное основание треугольника (частный случай расширенной стороны ) — это линия , содержащая основание. Когда треугольник тупой и основание выбрано в качестве одной из сторон, примыкающих к тупому углу , тогда высота, опущенная перпендикулярно от вершины к основанию, пересекает расширенное основание снаружи треугольника.

Площадь треугольника равна половине произведения основания на высоту (длину высоты). Для треугольника $\triangle ABC$ с противоположными сторонами $a,b,c,$ если три высоты треугольника называются $h_{a},h_{b},h_{c},$ площадь:

$\Delta ={\tfrac {1}{2}}ah_{a}={\tfrac {1}{2}}bh_{b}={\tfrac {1}{2}}ch_{c}.$

Учитывая фиксированную сторону основания и фиксированную площадь треугольника, геометрическое место вершин представляет собой прямую линию, параллельную основанию.

Трапеции или параллелограмма

можно считать любую из сторон параллелограмма или любую (но обычно более длинную) из параллельных сторон трапеции Его основанием . Иногда параллельную противоположную сторону также называют основанием , а иногда вершиной , вершиной или вершиной . Два других ребра можно назвать сторонами .

площади

Основания обычно используются (вместе с высотами) для расчета площадей и объемов фигур. Говоря об этих процессах, меру (длину или площадь) основания фигуры часто называют ее «основанием».

При таком использовании площадь параллелограмма или объем призмы или цилиндра можно вычислить, умножив его «основание» на высоту; аналогично площади треугольников и объемы конусов и пирамид представляют собой доли произведений их оснований и высот. Некоторые фигуры имеют два параллельных основания (например, трапеции и усеченные концы), оба из которых используются для расчета размеров фигур.