Изотоксальная фигура

В геометрии многогранник греческого например, многоугольник или многогранник ) или тайлинг является изотоксальным (от ( τόξον 'дуга') или реберно-транзитивным, если его симметрии действуют транзитивно на его ребрах . Неформально это означает, что у объекта есть только один тип ребра: для двух ребер существует перемещение , вращение и /или отражение, которое перемещает одно ребро к другому, оставляя область, занятую объектом, неизменной.

Изотоксальные полигоны

Изотоксальный многоугольник — это четный многоугольник, то есть равносторонний многоугольник , но не все равносторонние многоугольники являются изотоксальными. Двойники изогональными изотоксальных многоугольников являются многоугольниками . изотоксал $4n$ -гоны центрально симметричны , поэтому также являются зоногонами .

В общем, (нерегулярный) изотоксал $2n$ -гон имеет $\mathrm {D} _{n},(^{*}nn)$ двугранная симметрия . Например, (неквадратный) ромб — это изотоксал». $2$ × $2$ -гон" (четырехугольник) с $\mathrm {D} _{2},(^{*}22)$ симметрия. Все обычное ${\color {royalblue}n}$ -угольники (также с нечетным $n$ ) изотоксалы, имеющие вдвое больший минимальный порядок симметрии: регулярный $n$ -гон имеет $\mathrm {D} _{n},(^{*}nn)$ двугранная симметрия.

изотоксал ${\mathbf {2}}n$ -угольник с внешним внутренним углом $\alpha$ может быть обозначено $\{n_{\alpha }\}.$ Внутренний внутренний угол $(\beta )$ может быть меньше или больше, чем $180$ ${\color {royalblue}^{\mathsf {o}}},$ создание выпуклых или вогнутых многоугольников соответственно.

Звезда ${\color {royalblue}{\mathbf {2}}n}$ -gon также может быть изотоксалом, обозначаемым $\{(n/q)_{\alpha }\},$ с $q\leq n-1$ и с наибольшим общим делителем $\gcd(n,q)=1,$ где $q$ это число оборотов или плотность . ^[1] Вогнутые внутренние вершины могут быть определены для $q<n/2.$ Если $D=\gcd(n,q)\geq 2,$ затем $\{(n/q)_{\alpha }\}=\{(Dm/Dp)_{\alpha }\}$ «сводится» к сложному $D\{(m/p)_{\alpha }\}$ из $D$ повернутые копии $\{(m/p)_{\alpha }\}.$

Осторожность:

Вершины

\{(n/q)_{\alpha }\}

не всегда располагаются так, как у

\{n_{\alpha }\},

тогда как вершины регулярного

\{n/q\}

расположены как обычные

\{n\}.

набор «однородных» мозаик , на самом деле изогональных мозаик, Можно определить использующих изотоксальные многоугольники в качестве менее симметричных граней, чем обычные.

Примеры неправильных изотоксальных многоугольников и соединений
Количество сторон: $2n$	2×2 (Цент. сим.)	2×3	2×4 (Цент. сим.)	2×5	2×6 (Цент. сим.)	2×7	2×8 (Цент. сим.)
$\{n_{\alpha }\}$ Выпуклый: $\beta <180^{\circ }.$ Вогнутое: $\beta >180^{\circ }.$	$\{2_{\alpha }\}$	$\{3_{\alpha }\}$	$\{4_{\alpha }\}$	$\{5_{\alpha }\}$	$\{6_{\alpha }\}$	$\{7_{\alpha }\}$	$\{8_{\alpha }\}$
2-оборотный 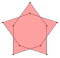$\{(n/2)_{\alpha }\}$	--	$\{(3/2)_{\alpha }\}$	$2\{2_{\alpha }\}$	$\{(5/2)_{\alpha }\}$	$2\{3_{\alpha }\}$	$\{(7/2)_{\alpha }\}$	$2\{4_{\alpha }\}$
3-оборотный $\{(n/3)_{\alpha }\}$	--	--	$\{(4/3)_{\alpha }\}$	$\{(5/3)_{\alpha }\}$	$3\{2_{\alpha }\}$	$\{(7/3)_{\alpha }\}$	$\{(8/3)_{\alpha }\}$
4-оборотный $\{(n/4)_{\alpha }\}$	--	--	--	$\{(5/4)_{\alpha }\}$	$2\{(3/2)_{\alpha }\}$	$\{(7/4)_{\alpha }\}$	$4\{2_{\alpha }\}$
5-оборотный $\{(n/5)_{\alpha }\}$	--	--	--	--	$\{(6/5)_{\alpha }\}$	$\{(7/5)_{\alpha }\}$	$\{(8/5)_{\alpha }\}$
6-поворотный $\{(n/6)_{\alpha }\}$	--	--	--	--	--	$\{(7/6)_{\alpha }\}$	$2\{(4/3)_{\alpha }\}$
7-поворотный $\{(n/7)_{\alpha }\}$	--	--	--	--	--	--	$\{(8/7)_{\alpha }\}$

Изотоксальные многогранники и мозаики

Правильные многогранники бывают изоэдральными (переходными по граням), изогональными (переходными по вершинам) и изотоксальными (переходными по ребрам).

Квазиправильные многогранники, такие как кубооктаэдр и икосододекаэдр , являются изогональными и изотоксальными, но не изоэдральными. Их двойники, в том числе ромбический додекаэдр и ромбический триаконтаэдр , изоэдральны и изотоксальны, но не изогональны.

Примеры
Квазирегулярный многогранник	Квазирегулярный двойной многогранник	Квазирегулярный звездный многогранник	Квазирегулярный двойной звездный многогранник	Квазирегулярный плитка	Квазирегулярный двойной плитка
Кубооктаэдр . – это изогональный и изотоксальный многогранник	Ромбический додекаэдр – это равногранный и изотоксальный многогранник.	Большой икосододекаэдр — изогональный и изотоксальный звездчатый многогранник.	Большой ромбический триаконтаэдр представляет собой равногранный и изотоксальный звездчатый многогранник.	Тригексагональная мозаика - это изогональная и изотоксальная мозаика.	Ромбическая мозаика представляет собой изоэдральную и изотоксальную мозаику с симметрией p6m (*632).

Не каждый многогранник или двумерная мозаика, построенная из правильных многоугольников, является изотоксальной. Например, усеченный икосаэдр (знакомый нам футбольный мяч) не является изотоксическим, поскольку у него есть два типа ребер: шестиугольник-шестиугольник и шестиугольник-пятиугольник, и симметрия твердого тела не позволяет переместить ребро шестиугольника-шестиугольника на ребро шестиугольника-шестиугольника. край шестиугольника-пятиугольника.

Изотоксальный многогранник имеет одинаковый двугранный угол для всех ребер.

Двойственный выпуклому многограннику также является выпуклым многогранником. ^[2]

Двойственный невыпуклому многограннику также является невыпуклым многогранником. ^[2] (По контрасту.)

Двойник изотоксального многогранника также является изотоксальным многогранником. (См. статью Двойной многогранник .)

Существует девять выпуклых изотоксальных многогранников: пять ( правильных ) Платоновых тел , два ( квазирегулярных ) общих ядра двойственных Платоновых тел и два их двойственных тела.

Существует четырнадцать невыпуклых изотоксальных многогранников: четыре (правильных) многогранника Кеплера–Пуансо , два (квазиправильных) общих ядра двойственных многогранников Кеплера–Пуансо и два их двойственных многогранника, а также три квазиправильных дитригональных (3 | pq ) звездчатых многогранника. , и их три двойника.

Существует по крайней мере пять изотоксальных полиэдрических соединений: пять правильных многогранных соединений ; их пять двойников также являются пятью правильными многогранными соединениями (или одним хиральным двойником).

Существует не менее пяти изотоксальных многоугольных мозаик евклидовой плоскости и бесконечно много изотоксальных многоугольных мозаик гиперболической плоскости, включая конструкции Витхоффа из регулярных гиперболических мозаик { p , q } и неправых ( pqr ) групп.

См. также

Ссылки

^ Плитки и узоры , Бранко Грюнбаум, Г.К. Шепард, 1987, 2.5 Плитки с использованием звездчатых многоугольников, стр. 82–85.
^ Jump up to: Перейти обратно: ^а ^б «двойственность» . maths.ac-noumea.nc . Проверено 30 сентября 2020 г.

Питер Р. Кромвель, Многогранники , Издательство Кембриджского университета, 1997, ISBN 0-521-55432-2 , Транзитивность, с. 371
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . (6.4 Изотоксальные мозаики, стр. 309–321)
Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, MS; Миллер, JCP (1954), «Равномерные многогранники», Философские труды Лондонского королевского общества. Серия A. Математические и физические науки , 246 (916): 401–450, Bibcode : 1954RSPTA.246..401C , doi : /rsta.1954.0003 , ISSN 0080-4614 , JSTOR 91532 , MR 0062446 , 202575183 10.1098

[1] Плитки и узоры , Бранко Грюнбаум, Г.К. Шепард, 1987, 2.5 Плитки с использованием звездчатых многоугольников, стр. 82–85.

[:0-2] Jump up to: Перейти обратно: ^а ^б «двойственность» . maths.ac-noumea.nc . Проверено 30 сентября 2020 г.

[1]

[2]