Гептадекагон
| Правильный семиугольник | |
|---|---|
 Правильный семиугольник | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 17 |
| Символ Шлефли | {17} |
| Диаграммы Кокстера – Дынкина | |
| Группа симметрии | Двугранник (Д 17 ), заказ 2×17 |
| Внутренний угол ( градусы ) | ≈158.82° |
| Характеристики | Выпуклый , циклический , равносторонний , изогональный , изотоксальный |
| Двойной полигон | Себя |
В геометрии семиугольник — , септадекагон или 17-угольник это семнадцатисторонний многоугольник .
Правильный семиугольник [ править ]
Правильный . семиугольник обозначается символом Шлефли {17}
Строительство [ править ]

Поскольку 17 — простое число Ферма , правильный семиугольник — это конструктивный многоугольник (то есть такой, который можно построить с помощью циркуля и немаркированной линейки ): это было показано Карлом Фридрихом Гауссом в 1796 году в возрасте 19 лет. [1] Это доказательство представляет собой первый прогресс в построении правильных многоугольников за более чем 2000 лет. [1] Доказательство Гаусса опирается, во-первых, на тот факт, что конструктивность эквивалентна выразимости тригонометрических функций общего угла через арифметические операции и извлечение квадратных корней , а во-вторых, на его доказательство того, что это можно сделать, если нечетные простые множители , количество сторон правильного многоугольника, представляют собой различные простые числа Ферма, которые имеют вид для некоторого неотрицательного целого числа . Таким образом, для построения правильного семиугольника необходимо найти косинус с точки зрения квадратных корней. Книга Гаусса Disquisitiones Arithmeticae. [2] дает это (в современных обозначениях) как [3]

Построения правильного треугольника , пятиугольника , пятиугольника и многоугольников с 2 час Евклид дал в раз больше сторон, но конструкции, основанные на простых числах Ферма, отличных от 3 и 5, были неизвестны древним. (Единственные известные простые числа Ферма — это F n для n = 0, 1, 2, 3, 4. Это 3, 5, 17, 257 и 65537.)
Явное построение семиугольника было дано Гербертом Уильямом Ричмондом в 1893 году. Следующий метод построения использует круги Карлейля , как показано ниже. Основываясь на построении правильного 17-угольника, можно легко построить n -угольников, где n является произведением 17 на 3 или 5 (или на то и другое) и любой степени двойки: правильный 51-угольник, 85-угольник или 255. -угольник и любой правильный n -угольник с 2 час раз больше сторон.


Другое построение правильного семиугольника с использованием линейки и циркуля выглядит следующим образом:

Т. П. Стоуэлл из Рочестера, штат Нью-Йорк, ответил на запрос WE Heal, Уилинг, Индиана, в журнале The Analyst в 1877 году: [5]
«Чтобы построить правильный многоугольник с семнадцатью сторонами в круге. Нарисуйте радиус СО под прямым углом к диаметру AB: На OC и OB примите OQ равным половине, а OD равным восьмой части радиуса: Сделайте DE и DF, каждый из которых равен DQ, а EG и FH соответственно равны EQ и FQ, принимают OK среднее, пропорциональное между OH и OQ, и через K проводят KM параллельно AB, встречаясь с полукругом, описанным на OG в M; до OC, разрезая данную окружность по N – дуга AN – это семнадцатая часть всей окружности».

«отправлено Т. П. Стоуэллом, зачислено в математический репозиторий Лейборна, 1818 г.» .
Добавлено: «Примите ОК среднее пропорциональное между OH и OQ».

«отправлено Т. П. Стоуэллом, зачислено в математический репозиторий Лейборна, 1818 г.» .
Добавлено: «примите ОК среднее пропорциональное между OH и OQ» , анимация.
Следующий простой дизайн принадлежит Герберту Уильяму Ричмонду в 1893 году: [6]
- «ПУСТЬ OA, OB (рис. 6) — два перпендикулярных радиуса окружности. Пусть OI составляет одну четвертую от OB, а угол OIE — одну четвертую от OIA; также найдите в ОА произведенную точку F такую, что EIF равна 45°. Пусть окружность AF диаметром разрезает OB в K, а окружность с центром E и радиусом EK пересекает OA в N 3 и N 5 , тогда если ординаты N 3 P 3 , N 5 P 5 ; к окружности проведены , дуги AP 3 , AP 5 составят 3/17 и 5/17 длины окружности».
- Точка N 3 очень близка к центральной точке теоремы Фалеса над AF.


Следующая конструкция является разновидностью конструкции HW Richmond.
Отличия от оригинала:
- Окружность k 2 определяет точку H вместо биссектрисы w 3 .
- Окружность к 4 вокруг точки G' (отражение точки G в m) дает точку N, уже не столь близкую к М, для построения касательной.
- Некоторые имена изменены.
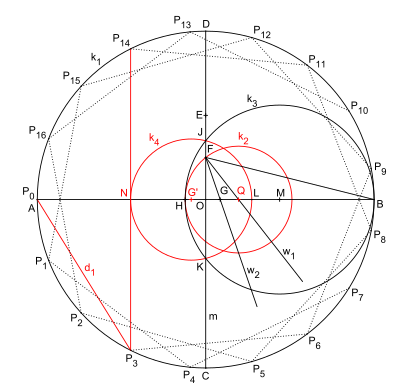
Другая, более поздняя конструкция, приведена Калладжи. [3]
вывод с использованием вложенных квадратных уравнений Тригонометрический
Объедините вложенную формулу двойного угла с формулой дополнительного угла, чтобы получить вложенный квадратичный полином ниже.
- , И
Поэтому,
Об упрощении и решении для X,
Точное значение греха и cos м π / (17 × 2 н ) [ редактировать ]
Если , и тогда в зависимости от любого целого числа m
Например, если m = 1
Вот выражения, упрощенные до следующей таблицы.
| м | 16 cos (м π / 17) | 8 грех (м π / 17) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Следовательно, применяя индукцию с m=1 и начиная с n=0:
- и
Симметрия [ править ]

Правильный семиугольник имеет Dih 17 симметрию , порядок 34. Поскольку 17 — простое число, существует одна подгруппа с диэдральной симметрией: Dih 1 и 2 циклических групп симметрии : Z 17 и Z 1 .
Эти 4 симметрии можно увидеть в 4 различных симметриях семиугольника. Джон Конвей маркирует их буквенным и групповым порядком. [7] Полная симметрия правильной формы равна r34 , отсутствие симметрии отмечено a1 . Двугранные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены буквой g в соответствии с их центральными порядками вращения.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g17 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Связанные многоугольники [ править ]
Гептадекаграммы [ править ]
Гептадекаграмма — это 17-гранный звездчатый многоугольник . имеют семь правильных форм Символы Шлефли : {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7} и {17/. 8}. Поскольку 17 — простое число, все это обычные звезды, а не составные числа.
| Картина |  {17/2} |  {17/3} |  {17/4} |  {17/5} |  {17/6} |  {17/7} |  {17/8} |
|---|---|---|---|---|---|---|---|
| Внутренний угол | ≈137.647° | ≈116.471° | ≈95.2941° | ≈74.1176° | ≈52.9412° | ≈31.7647° | ≈10.5882° |
Полигоны Петри [ править ]
Правильный семиугольник — это многоугольник Петри для одного правильного выпуклого многогранника более высокой размерности, спроецированного в косую ортогональную проекцию :
 16-симплекс (16Д) |
Ссылки [ править ]
- ^ Jump up to: а б Артур Джонс, Сидни А. Моррис, Кеннет Р. Пирсон, Абстрактная алгебра и знаменитые невозможности , Спрингер, 1991, ISBN 0387976612 , с. 178.
- ^ Карл Фридрих Гаусс « Арифметические исследования » eod book2ebooks, стр. 662 позиция 365
- ^ Jump up to: а б Калладжи, Джеймс Дж. « Центральный угол правильного 17-угольника », Mathematical Gazette 67, декабрь 1983 г., 290–292.
- ^ Дуэйн В. ДеТемпл «Круги Карлайла и простота Лемуана многоугольных конструкций» в The American Mathematical Monthly, том 98, выпуск 1 (февраль 1991 г.), 97–108. «4. Построение правильного семиугольника (17-угольника)», стр. 101–104, стр.103, документ из веб-архива, выбранный 28 января 2017 г.
- ^ Хендрикс, Дж. Э. (1877). «Ответ на вопрос г-на Хила; Т. П. Стоуэлл из Рочестера, штат Нью-Йорк» Аналитик: Ежемесячный журнал чистой и прикладной математики, том 1 : 94–95. Запрос, WE Heal, Уилинг, Индиана , с. 64; дата доступа 30 апреля 2017 г.
- ^ Герберт В. Ричмонд, описание иллюстрации «Конструкция правильного многоугольника с семнадцатью сторонами» (рис. 6) , The Quarterly Journal of Pure and Applied Mathematics 26: стр. 206–207. Проверено 4 декабря 2015 г.
- ^ Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275–278)
Дальнейшее чтение [ править ]
- Данэм, Уильям (сентябрь 1996 г.). «1996 год — тройной юбилей» . Математические горизонты . 4 : 8–13. дои : 10.1080/10724117.1996.11974982 . Проверено 6 декабря 2009 г.
- Кляйн, Феликс и др. Известные задачи и другие монографии . – Описывает алгебраический аспект Гаусса.
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Гептадекагон» . Математический мир . Содержит описание конструкции.
- «Построение семиугольника» . MathPages.com .
- Тригонометрические функции семиугольника
- Видео BBC о новом центре исследований и разработок SolarUK
- Архивировано в Ghostarchive и Wayback Machine : Эйзенбуд, Дэвид . «Удивительный семиугольник (17-угольник)» (Видео) . Брэйди Харан . Проверено 2 марта 2015 г.
- ОЭИС : A210644



































