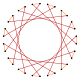
Триаконтагон

Правильный триаконтагон
Правильный триаконтагон
Тип	Правильный многоугольник
Ребра и вершины	30
Символ Шлефли	{30}, т{15}
Диаграммы Кокстера – Дынкина
Группа симметрии	Двугранник (Д 30 ), заказ 2×30
Внутренний угол ( градусы )	168°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии триаконтагон или 30-угольник — это тридцатигранный многоугольник . Сумма внутренних углов любого триаконтагона равна 5040 градусов.

Правильный триаконтагон

Правильный t триаконтагон представляет собой конструируемый многоугольник путем разделения ребра пополам правильного пятидесятиугольника , а также может быть построен как усеченный пятиугольник {15}. триаконтагон Усеченный t{30} является шестиугольником {60}.

Один внутренний угол в правильном триаконтагоне равен 168 градусам, то есть один внешний угол будет равен 12°. Триаконтагон — самый большой правильный многоугольник, внутренний угол которого равен сумме внутренних углов меньших многоугольников : 168° — это сумма внутренних углов равностороннего треугольника (60°) и правильного пятиугольника (108°).

Площадь t правильного триаконтагона равна (при = длине ребра )

$A={\frac {15}{2}}t^{2}\cot {\frac {\pi }{30}}={\frac {15}{4}}t^{2}\left({\sqrt {15}}+3{\sqrt {3}}+{\sqrt {2}}{\sqrt {25+11{\sqrt {5}}}}\right)$

Внутренний радиус правильного триаконтагона равен

$r={\frac {1}{2}}t\cot {\frac {\pi }{30}}={\frac {1}{4}}t\left({\sqrt {15}}+3{\sqrt {3}}+{\sqrt {2}}{\sqrt {25+11{\sqrt {5}}}}\right)$

Радиус описанной окружности правильного триаконтагона равен

$R={\frac {1}{2}}t\csc {\frac {\pi }{30}}={\frac {1}{2}}t\left(2+{\sqrt {5}}+{\sqrt {15+6{\sqrt {5}}}}\right)$

Строительство

Правильный трехугольник с заданной описанной окружностью. D — середина AM, DC = DF, а CF — длина стороны правильного пятиугольника — E ₂₅ E ₁ . Поскольку 1/30 = 1/5 - 1/6, разница между дугами, опирающимися на стороны правильного пятиугольника и шестиугольника (E ₂₅ E ₁ и E ₂₅ A), равна разнице правильного триаконтагона AE ₁ .

Поскольку 30 = 2 × 3 × 5, правильный трехугольник можно построить с помощью циркуля и линейки .

Симметрия

Симметрии правильного триаконтагона показаны цветами на краях и вершинах. Линии отражений имеют синий цвет через вершины и фиолетовый через края. Вращения обозначены числами в центре. Вершины окрашены в соответствии с их положением симметрии. Симметрии подгрупп соединены цветными линиями с индексами 2, 3 и 5.

Правильный триаконтагон имеет _{Dih 30} двугранную симметрию , порядка 60, представленную 30 линиями отражения. Dih ₃₀ имеет 7 двугранных подгрупп: Dih ₁₅ , (Dih ₁₀ , Dih ₅ ), (Dih ₆ , Dih ₃ ) и (Dih ₂ , Dih ₁ ). Он также имеет еще восемь циклических симметрий в виде подгрупп: (Z ₃₀ , Z ₁₅ ), (Z ₁₀ , Z ₅ ), (Z ₆ , Z ₃ ) и (Z ₂ , Z ₁ ), где Z _n представляет π/ n радианная вращательная симметрия.

Джон Конвей обозначает эти низшие симметрии буквой, и порядок симметрии следует за буквой. Он дает d (диагональ) с зеркальными линиями, проходящими через вершины, p с зеркальными линиями, проходящими через края (перпендикулярно), i с зеркальными линиями, проходящими как через вершины, так и через края, и g для вращательной симметрии. a1 обозначает отсутствие симметрии.

Эти более низкие симметрии допускают степень свободы в определении неправильных триаконтагонов. Только подгруппа g30 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Рассечение

30-угольник с 420 ромбами

Коксетер утверждает, что каждый зоногон (2- метровый угольник, противоположные стороны которого параллельны и одинаковой длины) можно разрезать на m ( m -1)/2 параллелограмма. В частности, это верно для правильных многоугольников с четным числом сторон, и в этом случае все параллелограммы являются ромбами. Для правильного триаконтагона = 15 m его можно разделить на 105: 7 наборов по 15 ромбов. Это разложение основано на многоугольника Петри проекции 15-куба .

Примеры

Триаконтаграмма

Триаконтаграмма — это 30-гранный звездчатый многоугольник (хотя слово встречается крайне редко). Существует 3 правильные формы, заданные символами Шлефли {30/7}, {30/11} и {30/13}, а также 11 составных звездных фигур с одинаковой конфигурацией вершин .

показывать Соединения и звезды
Form	Compounds					Star polygon	Compound
Picture	{30/2}=2{15}	{30/3}=3{10}	{30/4}=2{15/2}	{30/5}=5{6}	{30/6}=6{5}	{30/7}	{30/8}=2{15/4}
Interior angle	156°	144°	132°	120°	108°	96°	84°
Form	Compounds		Star polygon	Compound	Star polygon	Compounds
Picture	{30/9}=3{10/3}	{30/10}=10{3}	{30/11}	{30/12}=6{5/2}	{30/13}	{30/14}=2{15/7}	{30/15}=15{2}
Interior angle	72°	60°	48°	36°	24°	12°	0°

Существуют также изогональные триаконтаграммы, построенные как более глубокие усечения правильного пятиугольника {15} и пентадекаграммы {15/7}, а также перевернутые пентадекаграммы {15/11} и {15/13}. Остальные усечения образуют двойные покрытия: t{15/14}={30/14}=2{15/7}, t{15/8}={30/8}=2{15/4}, t{15/ 4}={30/4}=2{15/4} и t{15/2}={30/2}=2{15}.

показывать Соединения и звезды
Quasiregular	Isogonal							Quasiregular Double coverings
t{15} = {30}								t{15/14}=2{15/7}
t{15/7}={30/7}								t{15/8}=2{15/4}
t{15/11}={30/11}								t{15/4}=2{15/2}
t{15/13}={30/13}								t{15/2}=2{15}

Полигоны Петри

Правильный триаконтагон — это многоугольник Петри для трёх 8-мерных многогранников с симметрией E8 _, показанный в ортогональных проекциях на _{плоскость E8} Коксетера . Это также многоугольник Петри для двух 4-мерных многогранников, показанный на _{H 4} плоскости Кокстера .

E8			Ч 4
4 21	2 41	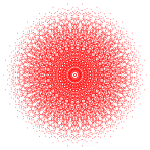1 42	120-ячеечный	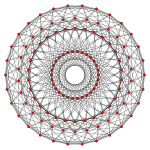600-ячеечный

Правильная триаконтаграмма {30/7} также является многоугольником Петри для великого звездчатого 120-клеточного и великого 600-клеточного .

Ссылки

• Именование многоугольников и многогранников
• триаконтагон