Тангенциальный четырехугольник

Касательный четырехугольник с вписанной в него окружностью

В евклидовой геометрии ( касательный четырехугольник иногда просто касательный четырехугольник ) или описанный четырехугольник — это выпуклый четырехугольник , все стороны которого могут касаться одной окружности внутри четырехугольника. Эта окружность называется вписанной в четырехугольник или вписанной окружностью, ее центр — вписанная окружность , а радиус — вписанный радиус . Поскольку эти четырехугольники можно нарисовать вокруг вписанных ими окружностей или описать их, их также называют описанными четырехугольниками , описанными четырехугольниками и описанными четырехугольниками . Касательные четырехугольники являются частным случаем касательных многоугольников .

Другие менее часто используемые названия для этого класса четырехугольников — вписываемый четырехугольник , вписываемый четырехугольник , вписываемый четырехугольник , описанный четырехугольник и социклический четырехугольник . Из-за риска путаницы с четырехугольником, имеющим описанную окружность, который называется вписанным четырехугольником или вписанным четырехугольником, предпочтительно не использовать ни одно из последних пяти названий.

Во всех треугольниках может быть вписанная окружность, но не во всех четырехугольниках. Примером четырехугольника, который не может быть касательным, является неквадратный прямоугольник . раздела В приведенных ниже характеристиках указано, каким необходимым и достаточным условиям должен удовлетворять четырехугольник, чтобы иметь возможность иметь вписанную окружность.

Особые случаи

Примерами тангенциальных четырехугольников являются воздушные змеи , в состав которых входят ромбы , которые, в свою очередь, включают квадраты . Воздушные змеи представляют собой в точности касательные четырехугольники, которые также являются ортодиагональными . Правильный кайт — это кайт с описанной окружностью . Если четырехугольник одновременно является касательным и вписанным , он называется бицентрическим четырехугольником , а если он одновременно является касательным и трапецией , он называется касательной трапецией .

Характеристики

В касательном четырехугольнике четыре биссектрисы встречаются в центре вписанной окружности. И наоборот, выпуклый четырехугольник, в котором четыре биссектрисы пересекаются в одной точке, должен быть касательным, а общая точка является центром.

Согласно теореме Пито , две пары противоположных сторон касательного четырехугольника в сумме дают одну и ту же общую длину, которая равна полупериметру s четырехугольника :

$a+c=b+d={\frac {a+b+c+d}{2}}=s.$

И наоборот, выпуклый четырехугольник, в котором a + c = b + d, должен быть касательным.

Если противоположные стороны в выпуклом четырехугольнике ABCD (который не является трапецией ) пересекаются в точках E и F , то он является касательным тогда и только тогда, когда любой из

$\displaystyle BE+BF=DE+DF$

или

$\displaystyle AE-EC=AF-FC:$

Другое необходимое и достаточное условие состоит в том, что выпуклый четырехугольник ABCD является касательным тогда и только тогда, когда вписанные окружности в двух треугольниках ABC и ADC касаются . друг друга

Характеристика углов, образованных диагональю BD и четырьмя сторонами четырехугольника ABCD, принадлежит Иосифеску. В 1954 году он доказал, что выпуклый четырёхугольник имеет вписанную окружность тогда и только тогда, когда

$\tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.$

Касательный четырехугольник (синий) с вписанной окружностью (пунктирная линия) и четырьмя касающимися снаружи окружностями (красным), каждая из которых касается данной стороны и продолжений соседних сторон.

Далее, выпуклый четырехугольник с последовательными сторонами a , b , c , d является касательным тогда и только тогда, когда

$R_{a}R_{c}=R_{b}R_{d}$

где Ra _и , Rb _Rc , a _Rd , , _{соответственно} — радиусы окружностей, касающихся снаружи сторон , b , c протяженность d , двух соседних сторон для каждой стороны.

Известны еще несколько характеристик четырех подтреугольников, образованных диагоналями.

Точки контакта и длины касательных

Тагенциальный четырехугольник (синий) и его контактный четырехугольник (зеленый), соединяющие четыре точки контакта между вписанной окружностью и сторонами. Также показаны хорды касания, соединяющие противоположные точки контакта (красным), и длины касательных по сторонам.

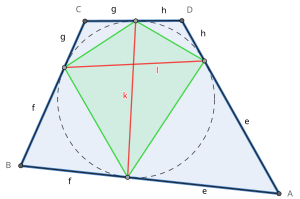
Вписанная окружность касается каждой стороны в одной точке контакта . Эти четыре точки определяют новый четырехугольник внутри исходного четырехугольника: контактный четырехугольник, который является циклическим, поскольку он вписан во вписанную окружность исходного четырехугольника.

Восемь касательных длин ( e , f , g , h на рисунке справа) касательного четырехугольника — это отрезки прямой от вершины до точек контакта. Из каждой вершины есть две конгруэнтные касательные длины.

Две хорды касания ( k и l на рисунке) касательного четырехугольника представляют собой отрезки, соединяющие точки контакта на противоположных сторонах. Это также диагонали контактного четырехугольника.

Площадь

Нетригонометрические формулы

Площадь K касательного четырехугольника определяется выражением

$\displaystyle K=r\cdot s,$

где s — полупериметр , а r — внутренний радиус . Другая формула

$\displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-(ac-bd)^{2}}}$

что дает площадь через диагонали p , q и стороны a , b , c , d касательного четырехугольника.

Площадь также можно выразить через четыре касательных длины . Если это e , f , g , h , то касательный четырехугольник имеет площадь

$\displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.$

Кроме того, площадь касательного четырехугольника можно выразить через стороны a, b, c, d и последовательные длины касательных e, f, g, h как

$K={\sqrt {abcd-(eg-fh)^{2}}}.$

Поскольку eg = fh тогда и только тогда, когда касательный четырехугольник также является циклическим и, следовательно, бицентрическим, это показывает, что максимальная площадь ${\sqrt {abcd}}$ происходит тогда и только тогда, когда касательный четырехугольник является бицентрическим.

Тригонометрические формулы

Тригонометрическая d формула площади через стороны a , b , c , и два противоположных угла:

$\displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}}.$

Для заданных длин сторон площадь максимальна , если четырехугольник также является вписанным и, следовательно, является вписанным четырехугольником . Затем $K={\sqrt {abcd}}$ так как противоположные углы являются дополнительными углами . Это можно доказать и другим способом, используя исчисление .

Другая формула площади касательного четырехугольника ABCD , включающего два противоположных угла:

$K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C}{2}}$

где я - центр.

Фактически площадь можно выразить через две смежные стороны и два противоположных угла:

$K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.$

Еще одна формула площади:

$K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,$

где θ — любой из углов между диагоналями. Эту формулу нельзя использовать, если касательный четырехугольник представляет собой воздушный змей, поскольку тогда θ равен 90 ° и функция тангенса не определена.

Неравенства

Как косвенно отмечено выше, площадь касательного четырёхугольника со сторонами a , b , c , d удовлетворяет условию

$K\leq {\sqrt {abcd}}$

с равенством тогда и только тогда, когда это вписанный четырехугольник .

По Т. А. Ивановой (1976 г.), полупериметр s касательного четырехугольника удовлетворяет условию

$s\geq 4r$

где r — внутренний радиус. Равенство существует тогда и только тогда, когда четырехугольник является квадратом . Это означает, что для площади K = rs имеет место неравенство

$K\geq 4r^{2}$

с равенством тогда и только тогда, когда касательный четырехугольник является квадратом.

Свойства раздела

Тангенциальный четырехугольник с внутренним радиусом r

Четыре отрезка между центром вписанной окружности и точками, где она касается четырехугольника, разделяют четырехугольник на четыре правильных воздушных змея .

Если линия разрезает касательный четырехугольник на два многоугольника с равными площадями и равными периметрами , то эта линия проходит через центр .

Инрадиус

Внутренний радиус в касательном четырехугольнике с последовательными сторонами a , b , c , d определяется выражением

$r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{b+d}}$

где K — площадь четырехугольника, а s — его полупериметр. Для касательного четырехугольника с заданными сторонами входящий радиус максимален , когда четырехугольник также является вписанным (и, следовательно, вписанным четырехугольником ).

С точки зрения касательных длин вписанная окружность имеет радиус

$\displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.$

Внутренний радиус также можно выразить через расстояния от центра I до вершин касательного четырехугольника ABCD . Если u = AI , v = BI , x = CI и y = DI , то

$r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}}$

где $\sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)$.

окружности Если вписанные в треугольники ABC , BCD , CDA , DAB имеют радиусы $r_{1},r_{2},r_{3},r_{4}$ соответственно, тогда радиус касательного четырехугольника ABCD определяется выражением

$r={\frac {G+{\sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}}$

где $G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}$.

Формулы углов

Если e , f , g и h — длины касательных от вершин A , B , C и D соответственно к точкам, где вписанная окружность касается сторон касательного четырехугольника ABCD , то углы четырехугольника можно вычислить по формуле

$\sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},$

$\sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},$

$\sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},$

$\sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.$

Угол между хордами касания k и l определяется выражением

$\sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.$

Диагонали

Если e , f , g и h — касательных длины A , B , C и D соответственно к точкам, где вписанная окружность касается сторон касательного четырехугольника ABCD , то длины диагоналей p = AC и q = БД являются

$\displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\Big (}(e+g)(f+h)+4fh{\Big )}}},$

$\displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.$

Касательные аккорды

Если e , f , g и h — касательные длины касательного четырехугольника, то длины касательных хорд равны

$\displaystyle k={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},$

$\displaystyle l={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}$

где хорда касания длины k соединяет стороны длин a = e + f и c = g + h , а хорда длины l соединяет стороны длин b = f + g и d = h + e . Квадрат отношения хорд касания удовлетворяет

${\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.$

Две касательные хорды

• перпендикулярны тогда и только тогда , когда касательный четырехугольник также имеет описанную окружность (он бицентричен ).
• имеют равные длины тогда и только тогда, когда касательный четырехугольник является воздушным змеем .

Хорда касания между сторонами AB и CD в касательном четырёхугольнике ABCD длиннее хорды между сторонами BC и DA тогда и только тогда, когда бимедиана между сторонами AB и CD короче, чем хорда между сторонами BC и DA .

Если касательный четырехугольник ABCD имеет точки касания W на AB и Y на CD , и если хорда касания WY пересекает диагональ BD в точке M , то отношение длин касательных ${\tfrac {BW}{DY}}$ равно отношению ${\tfrac {BM}{DM}}$ отрезков диагонали BD .

Коллинеарные точки

Построение линии Ньютона (красным цветом) касательного четырехугольника (синим цветом), показывающее совмещение центра I , средних точек диагоналей М ₁ и М ₂ и середины М ₃ соединяющегося отрезка JK (зеленого цвета). пересечение противоположных сторон.

Если M ₁ и M ₂ являются серединами диагоналей AC и BD соответственно в касательном четырехугольнике ABCD с центром I , и если пары противоположных сторон встречаются в точках J и K , причем M ₃ является серединой JK , то точки M ₃ , M1 _одной , I и M2 _лежат на прямой . Линия, содержащая их, является линией Ньютона четырехугольника.

Если продолжения противоположных сторон касательного четырехугольника пересекаются в точках J и K , а продолжения противоположных сторон в его контактном четырехугольнике пересекаются в точках L и M , то четыре точки J , L , K и M лежат на одной прямой.

Тангенциальный четырехугольник разделен на четыре треугольника, пересекающихся в центре I , их ортоцентры (фиолетовый цвет) и пересечение диагоналей P (зеленый цвет) лежат на одной прямой.

Если вписанная окружность касается сторон AB , BC , CD , DA в точках T ₁ , T ₂ , T ₃ , T ₄ соответственно и если N ₁ , N ₂ , N ₃ , N ₄ являются изотомическими сопряжениями этих точек с относительно соответствующих сторон (т. е. AT ₁ = BN ₁ и т. д.), то точка Нагеля касательного четырехугольника определяется как пересечение прямых N ₁ N ₃ и N ₂ N ₄ . Обе эти прямые делят периметр четырехугольника на две равные части. Что еще более важно, точка Нагеля N , «центр тяжести площади» G и центр тяжести I лежат на одной прямой в этом порядке, и NG = 2 GI . Эта линия называется линией Нагеля касательного четырехугольника.

касательном четырехугольнике ABCD с центром I и диагональю, пересекающейся в точке P , пусть H _X , HY _W , H _Z , H _В будут ортоцентрами треугольников AIB , BIC , CID , DIA . Тогда точки P , H _X , HY _W , H _Z , H _{лежат на одной} прямой.

Параллельные и перпендикулярные линии

Две диагонали и две хорды касания совпадают . Один из способов увидеть это — это предельный случай теоремы Брианшона , которая утверждает, что шестиугольник, все стороны которого касаются одного конического сечения, имеет три диагонали, которые пересекаются в одной точке. Из касательного четырехугольника можно сформировать шестиугольник с двумя углами 180 °, разместив две новые вершины в двух противоположных точках касания; все шесть сторон этого шестиугольника лежат на прямых, касающихся вписанной окружности, поэтому его диагонали сходятся в одной точке. Но две из этих диагоналей такие же, как диагонали касательного четырехугольника, а третья диагональ шестиугольника есть линия, проходящая через две противоположные точки касания. Повторение того же рассуждения с двумя другими точками касания завершает доказательство результата.

Если продолжения противоположных сторон касательного четырехугольника пересекаются в точках J и K , а диагонали пересекаются в точке P , то JK перпендикулярен продолжению IP , где I — центр.

Инцентр

Центр касательного четырехугольника лежит на его линии Ньютона (соединяющей середины диагоналей).

Отношение двух противоположных сторон в касательном четырехугольнике можно выразить через расстояния между центром I и вершинами согласно формуле

${\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}}.$

Произведение двух смежных сторон касательного четырехугольника ABCD с центром I удовлетворяет условию

$AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.$

Если I — центр касательного четырехугольника ABCD , то

$IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.$

Центр I в касательном четырехугольнике ABCD совпадает с «центроидом вершины» четырехугольника тогда и только тогда, когда

$IA\cdot IC=IB\cdot ID.$

Если M _p и M _q — середины диагоналей AC и BD соответственно в касательном четырехугольнике ABCD с центром I , то

${\frac {IM_{p}}{IM_{q}}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}$

где e , f , g и h — касательные длины в точках A , B , C и D соответственно. Объединив первое равенство с предыдущим свойством, «центр тяжести вершины» касательного четырехугольника совпадает с центром в том и только в том случае, если центр является серединой отрезка, соединяющего середины диагоналей.

Если четырехзвенную связь выполнить в виде касательного четырехугольника, то она останется касательной, как бы ни изгибалась связь, при условии, что четырехугольник останется выпуклым. (Так, например, если квадрат деформировать в ромб, он останется касательным, хотя и к меньшей вписанной окружности). Если одну сторону удерживать в фиксированном положении, то при изгибе четырехугольника центр очерчивает окружность радиуса ${\sqrt {abcd}}/s$ где a,b,c,d — стороны последовательности, а s — полупериметр.

Характеристики четырех подтреугольников

Характеристика Чао и Симеонова с точки зрения радиусов кругов внутри каждого из четырех треугольников.

В непересекающихся треугольниках APB , BPC , CPD , DPA, образованных диагоналями выпуклого четырехугольника ABCD , где диагонали пересекаются в точке P , существуют следующие характеристики касательных четырехугольников.

Пусть r1 _r3 , r2 _{треугольниках} , , _и и r4 _{соответственно} радиусы вписанных окружностей в APB BPC , CPD DPA обозначают четырех . Чао и Симеонов доказали, что четырехугольник касается касательной тогда и только тогда, когда

${\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.$

Эта характеристика уже была доказана пятью годами ранее Вайнштейном. Аналогичную характеристику при решении его задачи дали Васильев и Сендеров. Если h ₁ , h ₂ , h ₃ и h ₄ обозначают высоты в одних и тех же четырех треугольниках (от пересечения диагоналей до сторон четырехугольника), то четырехугольник является касательным тогда и только тогда, когда

${\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}.$

аналогичная характеристика касается эксрадиусов ra _в , r _b , rc _rd и . _Другая тех же четырех треугольниках (каждая из четырех вписанных окружностей касается одной стороны четырехугольника и продолжений его диагоналей) Четырехугольник является касательным тогда и только тогда, когда

${\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1}{r_{d}}}.$

Если R1 _, , R2 _{окружностей} , R3 _и и R4 _тогда обозначают радиусы описанных треугольников APB , BPC , CPD когда DPA соответственно , то четырехугольник ABCD является касательным тогда и только

$R_{1}+R_{3}=R_{2}+R_{4}.$

В 1996 году Вайнштейн, вероятно, был первым, кто доказал еще одну красивую характеристику касательных четырехугольников, которая позже появилась в нескольких журналах и на веб-сайтах. Он утверждает, что когда выпуклый четырехугольник делится своими двумя диагоналями на четыре непересекающихся треугольника, то центры четырех треугольников лежат на одной окружности тогда и только тогда, когда четырехугольник является касательным. Фактически центры образуют ортодиагональный вписанный четырехугольник . Связанный с этим результат состоит в том, что вписанные окружности можно заменить на вписанные в одни и те же треугольники (касательные к сторонам четырехугольника и продолжениям его диагоналей). Таким образом, выпуклый четырехугольник является касательным тогда и только тогда, когда эксцентры в этих четырех вписанных окружностях являются вершинами вписанного четырехугольника .

Выпуклый четырехугольник ABCD с диагоналями, пересекающимися в точке P , является касательным тогда и только тогда, когда четыре эксцентра в треугольниках APB , BPC , CPD и DPA , противоположные вершинам B и D, лежат на одной окружности. Если R _a , R _b , R _c и R _d являются эксрадиусами в треугольниках APB , BPC , CPD и DPA соответственно напротив вершин B и D , то еще одно условие состоит в том, что четырехугольник является касательным тогда и только тогда, когда

${\frac {1}{R_{a}}}+{\frac {1}{R_{c}}}={\frac {1}{R_{b}}}+{\frac {1}{R_{d}}}.$

Далее, выпуклый четырехугольник ABCD с диагоналями, пересекающимися в точке P, является касательным тогда и только тогда, когда

${\frac {a}{\triangle (APB)}}+{\frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}$

где ∆( APB ) — площадь треугольника APB .

Обозначим отрезки, на которые диагональное пересечение P делит диагональ AC , как AP = p ₁ и PC = p ₂ , и аналогично P делит диагональ BD на отрезки BP = q ₁ и PD = q ₂ . Тогда четырёхугольник является касательным тогда и только тогда, когда верно любое из следующих равенств:

$ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}$

или

${\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}$

или

${\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.$

при которых касательный четырехугольник может быть другим типом

Ромб

Касательный четырехугольник является ромбом тогда и только тогда, когда его противоположные углы равны.

Кайт

Касательный четырехугольник является воздушным змеем тогда и только тогда, когда выполняется любое из следующих условий:

• Площадь равна половине произведения диагоналей .
• Диагонали перпендикулярны .
• Два отрезка линии, соединяющие противоположные точки касания, имеют одинаковую длину.
• Одна пара противоположных касательных имеет одинаковую длину.
• Бимедианы имеют одинаковую длину.
• Произведения противоположных сторон равны.
• Центр вписанной окружности лежит на диагонали, которая является осью симметрии.

Бицентрический четырёхугольник

Бицентрический четырехугольник ABCD : контактный четырехугольник (розовый) ортодиагонален.

Если вписанная окружность касается сторон AB , BC , CD , DA в точках W , X , Y , Z соответственно, то касательный четырехугольник ABCD также является циклическим (и, следовательно, бицентрическим ) тогда и только тогда, когда выполняется любое из следующих условий:

• WY перпендикулярен XZ
• $AW\cdot CY=BW\cdot DY$
• ${\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}$

Первое из этих трех означает, что контактный четырехугольник WXYZ является ортодиагональным четырехугольником .

Касательный четырехугольник является бицентрическим тогда и только тогда, когда его внутренний радиус больше, чем у любого другого касательного четырехугольника, имеющего ту же последовательность длин сторон.

Тангенциальная трапеция

Если вписанная окружность касается сторон AB и CD в точках W и Y соответственно, то касательный четырехугольник ABCD также является трапецией с параллельными сторонами AB и CD тогда и только тогда, когда

$AW\cdot DY=BW\cdot CY$

а AD и BC — параллельные стороны трапеции тогда и только тогда, когда

$AW\cdot BW=CY\cdot DY.$

См. также

• Описанный круг
• Экстангенциальный четырехугольник
• Тангенциальный треугольник
• Тангенциальный многоугольник

Внешние ссылки

• Вайсштейн, Эрик В. , «Касательный четырехугольник» , MathWorld