линия Ньютона
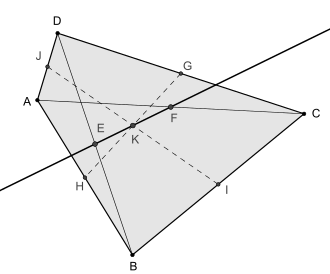
В евклидовой геометрии линия Ньютона — это линия, соединяющая середины двух диагоналей выпуклого параллельными четырехугольника с не более чем двумя сторонами . [1]
Свойства [ править ]
Отрезки , GH и IJ соединяющие середины противоположных сторон ( бимедианы ) выпуклого четырехугольника, пересекаются в точке, лежащей на прямой Ньютона. Эта точка K делит пополам отрезок EF , соединяющий середины диагоналей. [1]
По теореме Анны и ее обратной стороне любая внутренняя точка P на линии Ньютона четырехугольника ABCD обладает свойством, что
![{\displaystyle [\triangle ABP]+[\triangle CDP]=[\triangle ADP]+[\triangle BCP],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab69931aa3134a0fab625b8bb56e61978926d8b)
где [△ ABP ] обозначает площадь треугольника △ ABP . [2]
Если четырехугольник является касательным четырехугольником , то его центр также лежит на этой прямой. [3]
См. также [ править ]
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б Альсина, Клауди; Нельсен, Роджер Б. (2010). Очаровательные доказательства: путешествие в элегантную математику . Математическая ассоциация Америки . стр. 108–109. ISBN 9780883853481 .
- ^ Альсина и Нельсен (2010) , стр. 101-1. 116–117 .
- ^ Джукич, Душан; Янкович, Владимир; Матич, Иван; Петрович, Никола (2006). Сборник ИМО: сборник задач, предложенных для международных математических олимпиад: 1959–2004 гг . Спрингер. стр. 15. дои : 10.1007/0-387-33430-0 .
Внешние ссылки [ править ]
- Вайсштейн, Эрик В. «Теорема Леона Анны» . Математический мир .
- Александр Богомольный : Бимедианы в четырехугольнике на сайте Cut-the-knot.org