Линия Ньютона – Гаусса

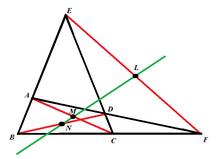
В геометрии линия Ньютона –Гаусса (или линия Гаусса–Ньютона ) — это линия, соединяющая середины трех диагоналей полного четырехугольника .

Середины двух диагоналей выпуклого четырехугольника с не более чем двумя параллельными сторонами различны и, таким образом, определяют линию, линию Ньютона . Если стороны такого четырехугольника продлены до полного четырехугольника, диагонали четырехугольника остаются диагоналями полного четырехугольника, а линия Ньютона четырехугольника является линией Ньютона – Гаусса полного четырехугольника.

Полные четырехугольники

Любые четыре прямые в общем положении (никакие две прямые не параллельны и никакие три не совпадают) образуют полный четырехугольник . Эта конфигурация состоит всего из шести точек, точек пересечения четырех линий, по три точки на каждой линии и ровно по две линии, проходящие через каждую точку. ^[1] Эти шесть точек можно разбить на пары так, чтобы отрезки линий, определенные какой-либо парой, не пересекали ни одну из данных четырех линий, кроме как в конечных точках. Эти три отрезка называются диагоналями полного четырехугольника.

Существование линии Ньютона-Гаусса.

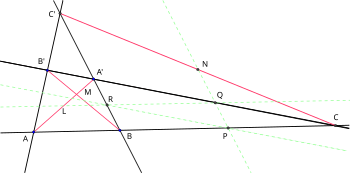
Хорошо известна теорема о том, что три середины диагоналей полного четырехугольника лежат на одной прямой . ^[2]Существует несколько доказательств результата, основанных на областях ^[2] или клиновые изделия ^[3] или, как следующее доказательство, на теореме Менелая , принадлежащей Хиллеру и опубликованной в 1920 году. ^[4]

Пусть полный четырехугольник $ABCA'B'C'$ обозначен, как на схеме, диагоналями $AA', BB', CC'$ и соответствующими средними точками $L, M,$ N. Пусть середины $BC, CA', A'B$ будут $P, Q, R$ соответственно. видно, что $QR$ пересекает $AA'$ в точке $L$ , $RP$ пересекает $BB'$ в точке $M$ и $PQ$ пересекает $CC'$ в точке $N.$ Используя подобные треугольники , Опять же, подобные треугольники обеспечивают следующие пропорции:

{\frac {\overline {RL}}{\overline {LQ}}}={\frac {\overline {BA}}{\overline {AC}}},\quad {\frac {\overline {QN}}{\overline {NP}}}={\frac {\overline {A'C'}}{\overline {C'B}}},\quad {\frac {\overline {PM}}{\overline {MR}}}={\frac {\overline {CB'}}{\overline {B'A'}}}.

Однако прямая $A'B'C$ пересекает стороны треугольника $△ ABC$ , поэтому по теореме Менелая произведение членов в правых частях равно −1. Таким образом, произведение слагаемых в левых частях также равно −1, и снова по теореме Менелая точки $L, M, N$ лежат на одной прямой на сторонах треугольника $△ PQR$ .

Приложения к вписанным четырехугольникам

Ниже приведены некоторые результаты, в которых используется линия Ньютона-Гаусса полных четырехугольников, связанных с циклическими четырехугольниками , на основе работ Барбу и Патраску. ^[5]

Равные углы

Для любого вписанного четырехугольника $ABCD$ пусть точка $F$ будет точкой пересечения двух диагоналей $AC$ и $BD$ . Продлите диагонали $AB$ и $CD$ до тех пор, пока они не встретятся в точке $E.$ пересечения Пусть середина отрезка EF $($ будет $N$ , а середина отрезка $BC$ будет $M$ рис. 1).

Теорема

Если середина отрезка $BF$ равна $P$ , линия Ньютона–Гаусса полного четырехугольника $ABCDEF$ и линия $PM$ определяют угол $∠ PMN,$ равный $∠ EFD$ .

Доказательство

Сначала докажем, что △ $NPM, △ EDF$ подобны треугольники .

Поскольку $BE ∥ PN$ и $FC ∥ PM$ , мы знаем, $что ∠ NPM = ∠ EAC$ . Также, ${\tfrac {\overline {BE}}{\overline {PN}}}={\tfrac {\overline {FC}}{\overline {PM}}}=2.$

Во вписанном четырехугольнике $ABCD$ выполняются следующие равенства :

{\begin{aligned}\angle EDF&=\angle ADF+\angle EDA,\\&=\angle ACB+\angle ABC,\\&=\angle EAC.\end{aligned}}

Следовательно, $∠ NPM = ∠ EDF$ .

Пусть $R 1, R 2$ — радиусы описанных окружностей △ $FCD EDB, △ соответственно$ . Примените закон синусов к треугольникам, чтобы получить:

{\frac {\overline {BE}}{\overline {FC}}}={\frac {2R_{1}\sin \angle EDB}{2R_{2}\sin \angle FDC}}={\frac {R_{1}}{R_{2}}}={\frac {2R_{1}\sin \angle EBD}{2R_{2}\sin \angle FCD}}={\frac {\overline {DE}}{\overline {DF}}}.

Поскольку $BE = 2 \cdot PN$ и $FC = 2 \cdot PM$ , это показывает равенство ${\tfrac {\overline {PN}}{\overline {PM}}}={\tfrac {\overline {DE}}{\overline {DF}}}.$ Отсюда следует подобие треугольников $△ PMN, △ DFE$ и $∠ NMP = ∠ EFD$ .

Примечание

Если $Q$ — середина отрезка $FC$ , то по тем же рассуждениям следует, что $∠ NMQ = ∠ EFA$ .

Изогональные линии

Теорема

Линия, проходящая через $E,$ параллельная линии Ньютона – Гаусса полного четырехугольника $ABCDEF$ , и линия $EF$ являются изогональными линиями $∠ BEC$ , то есть каждая линия является отражением другой относительно биссектрисы угла . ^[5] (рис. 2)

Доказательство

Треугольники $△ EDF, △ NPM$ подобны согласно приведенному выше рассуждению, поэтому $∠ DEF = ∠ PNM$ . Пусть $E'$ будет точкой пересечения $BC$ и линии, параллельной линии Ньютона – Гаусса $NM,$ проходящей через $E$ .

Поскольку $PN ∥ BE$ и $NM ∥ EE',$ $∠ BEF = ∠ PNF$ и $∠ FNM = ∠ E'EF$ .

Поэтому,

{\begin{aligned}\angle CEE'&=\angle DEF-\angle E'EF,\\&=\angle PNM-\angle FNM,\\&=\angle PNF=\angle BEF.\end{aligned}}

Два вписанных четырехугольника, разделяющие линию Ньютона-Гаусса.

Лемма

Пусть $G$ и $H$ — ортогональные проекции точки $F$ на прямые $AB$ и $CD$ соответственно.

Четырехугольники MPGN $MQHN$ и $.$ являются вписанными четырехугольниками ^[5]

Доказательство

$∠ EFD = ∠ PMN$ , как было показано ранее. Точки $P$ и $N$ являются центрами описанных окружностей прямоугольных треугольников $△ BFG, △ EFG$ соответственно . Таким образом, $∠ PGF = ∠ PFG$ и $∠ FGN = ∠ GFN$ .

Поэтому,

{\begin{aligned}\angle PGN+\angle PMN&=(\angle PGF+\angle FGN)+\angle PMN\\[4pt]&=\angle PFG+\angle GFN+\angle EFD\\[4pt]&=180^{\circ }\end{aligned}}.

Следовательно, $MPGN$ — вписанный четырехугольник, и по тем же соображениям $MQHN$ также лежит на окружности.

Теорема

Продлите линии $GF, HF$ так, чтобы они пересекали $EC, EB$ в точках $I, J$ соответственно (рис. 4).

Полные четырехугольники $EFGHIJ$ и $ABCDEF$ имеют одну и ту же линию Ньютона–Гаусса. ^[5]

Доказательство

Два полных четырехугольника имеют общую диагональ $EF$ . $N$ лежит на линии Ньютона – Гаусса обоих четырехугольников. $N$ равноудалён вписанного от $G$ и $H$ , так как это центр описанной окружности четырёхугольника $EGFH$ .

Если треугольники $△ GMP, △ HMQ$ конгруэнтны , то из этого следует, что $M$ лежит на биссектрисе прямой $HG$ . Следовательно, линия $MN$ содержит середину $GH$ и является линией Ньютона – Гаусса $EFGHIJ$ .

Чтобы показать, что треугольники $△ GMP, △ HMQ$ конгруэнтны, сначала заметим, что $PMQF$ — параллелограмм , поскольку точки $M, P$ являются серединами $BF, BC$ соответственно.

Поэтому,

{\begin{aligned}&{\overline {MP}}={\overline {QF}}={\overline {HQ}},\\&{\overline {GP}}={\overline {PF}}={\overline {MQ}},\\&\angle MPF=\angle FQM.\end{aligned}}

Также обратите внимание, что

\angle FPG=2\angle PBG=2\angle DBA=2\angle DCA=2\angle HCF=\angle HQF.

Следовательно,

{\begin{aligned}\angle MPG&=\angle MPF+\angle FPG,\\&=\angle FQM+\angle HQF,\\&=\angle HQF+\angle FQM,\\&=\angle HQM.\end{aligned}}

Следовательно, $△ GMP$ и $△ HMQ$ совпадают по SAS.

Примечание

Поскольку $△ GMP, △ HMQ$ являются конгруэнтными треугольниками, их описанные окружности $MPGN и MQHN$ также конгруэнтны .

История

Доказательство линии Ньютона-Гаусса было разработано двумя математиками, в честь которых оно названо: сэром Исааком Ньютоном и Карлом Фридрихом Гауссом . ^{[ нужна ссылка ]} Первоначальная основа этой теоремы взята из работы Ньютона в его предыдущей теореме о линии Ньютона , в которой Ньютон показал, что центр коники, вписанной в четырехугольник, лежит на линии Ньютона-Гаусса. ^[6]

Теорема Гаусса и Боденмиллера утверждает, что три окружности, диаметры которых являются диагоналями полного четырехугольника, соосны . ^[7]

Примечания

^ Альперин, Роджер К. (6 января 2012 г.). «Линии Гаусса – Ньютона и одиннадцатиточечные коники» . Исследовательские ворота .
^ Jump up to: ^а ^б Джонсон 2007 , с. 62
^ Педо, Дэн (1988) [1970], Комплексный курс геометрии , Дувр, стр. 46–47, ISBN 0-486-65812-0
^ Джонсон 2007 , с. 152
^ Jump up to: ^а ^б ^с ^д Патраску, Ион. «Некоторые свойства линии Ньютона – Гаусса» (PDF) . Форум Геометрикорум . Проверено 29 апреля 2019 г.
^ Уэллс, Дэвид (1991), Словарь любопытной и интересной геометрии Penguin , Penguin Books, стр. 36 , ISBN 978-0-14-011813-1
^ Джонсон 2007 , с. 172

Ссылки

Джонсон, Роджер А. (2007) [1929], Расширенная евклидова геометрия , Дувр, ISBN 978-0-486-46237-0
- (доступно онлайн как) Джонсон, Роджер А. (1929). «Современная геометрия: элементарный трактат о геометрии треугольника и круга» . ХатиТраст . Проверено 28 мая 2019 г.

Внешние ссылки

Богомонлый, Александр. «Теорема о полном четырехугольнике: что это такое?» . Проверено 11 мая 2019 г.

[:1-1] Альперин, Роджер К. (6 января 2012 г.). «Линии Гаусса – Ньютона и одиннадцатиточечные коники» . Исследовательские ворота .

[Johson62-2] Jump up to: ^а ^б Джонсон 2007 , с. 62

[3] Педо, Дэн (1988) [1970], Комплексный курс геометрии , Дувр, стр. 46–47, ISBN 0-486-65812-0

[4] Джонсон 2007 , с. 152

[:2-5] Jump up to: ^а ^б ^с ^д Патраску, Ион. «Некоторые свойства линии Ньютона – Гаусса» (PDF) . Форум Геометрикорум . Проверено 29 апреля 2019 г.

[6] Уэллс, Дэвид (1991), Словарь любопытной и интересной геометрии Penguin , Penguin Books, стр. 36 , ISBN 978-0-14-011813-1

[7] Джонсон 2007 , с. 172

[1]

[2]

[3]

[4]

[5]

[6]

[7]