деление пополам

Линия DE делит пополам линию AB в точке D, линия EF является биссектрисой отрезка AD в точке C, а линия EF является внутренней биссектрисой прямого угла AED.

В геометрии бисекция — это разделение чего-либо на две равные или конгруэнтные части (имеющие одинаковую форму и размер). Обычно это включает в себя биссектрису , также называемую биссектрисой . Наиболее часто рассматриваемыми видами биссектрис являются биссектриса отрезка проходящая через середину данного отрезка , и биссектриса угла — линия, проходящая через вершину угла — линия , (делящая его на два равных угла).В трехмерном пространстве обычно выполняется биссектрисой деление пополам , также называемой биссектрисой .

Биссектриса перпендикулярного отрезка [ править ]

Определение [ править ]

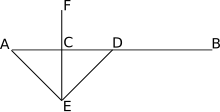
Биссектриса отрезка прямой — это линия, которая перпендикулярно пересекает отрезок в его средней точке .
Биссектриса отрезка прямой $AB$ также обладает тем свойством, что каждая его точка $X$ равноудален от концов сегмента AB:

(Д) $\quad |XA|=|XB|$ .

Доказательство следует из и теорема Пифагора :

|XA|^{2}=|XM|^{2}+|MA|^{2}=|XM|^{2}+|MB|^{2}=|XB|^{2}\;.

Свойство (D) обычно используют для построения биссектрисы:

Построение с помощью линейки и циркуля [ править ]

В классической геометрии биссекция представляет собой простую конструкцию циркуля и линейки , возможность которой зависит от умения рисовать дуги равных радиусов и разных центров:

Сегмент $AB$ делится пополам путем рисования пересекающихся кругов одинакового радиуса $r>{\tfrac {1}{2}}|AB|$ , центры которого являются концами отрезка. Линия, определяемая точками пересечения двух окружностей, является серединным перпендикуляром отрезка.
Потому что построение биссектрисы производится без знания середины отрезка. $M$ , конструкция используется для определения $M$ как пересечение биссектрисы и отрезка.

Эта конструкция фактически используется при построении линии, перпендикулярной данной прямой. $g$ в данный момент $P$ : рисование круга, центр которого находится $P$ так, что она пересекает линию $g$ в двух точках $A,B$ , а перпендикуляр, который нужно построить, — это один биссектрисный отрезок $AB$ .

Уравнения [ править ]

Если ${\vec {a}},{\vec {b}}$ — векторы положения двух точек $A,B$ , то его середина равна $M:{\vec {m}}={\tfrac {{\vec {a}}+{\vec {b}}}{2}}$ и вектор ${\vec {a}}-{\vec {b}}$ - вектор нормали к биссектрисе перпендикулярного отрезка. Следовательно, его векторное уравнение имеет вид $({\vec {x}}-{\vec {m}})\cdot ({\vec {a}}-{\vec {b}})=0$ . Вставка ${\vec {m}}=\cdots$ и расширение уравнения приводит к векторному уравнению

(V) $\quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).$

С $A=(a_{1},a_{2}),B=(b_{1},b_{2})$ получаем уравнение в координатной форме:

(С) $\quad (a_{1}-b_{1})x+(a_{2}-b_{2})y={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2})\;.$

Или явно:
(И) $\quad y=m(x-x_{0})+y_{0}$ ,
где $\;m=-{\tfrac {b_{1}-a_{1}}{b_{2}-a_{2}}}$ , $\;x_{0}={\tfrac {1}{2}}(a_{1}+b_{1})\;$ , и $\;y_{0}={\tfrac {1}{2}}(a_{2}+b_{2})\;$ .

Приложения [ править ]

Биссектрисы перпендикулярных отрезков использовались при решении различных геометрических задач:

Построение центра фалесова круга ,
Построение центра вписанной окружности треугольника,
Границы диаграммы Вороного состоят из отрезков таких линий или плоскостей.

Биссектрисы перпендикулярных отрезков в пространстве [ править ]

Биссектриса отрезка прямой представляет собой плоскость , которая перпендикулярно пересекает отрезок в его средней точке .

Его векторное уравнение буквально такое же, как и в плоском случае:

(V) $\quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).$

С $A=(a_{1},a_{2},a_{3}),B=(b_{1},b_{2},b_{3})$ получаем уравнение в координатной форме:

(С3) $\quad (a_{1}-b_{1})x+(a_{2}-b_{2})y+(a_{3}-b_{3})z={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}+a_{3}^{2}-b_{3}^{2})\;.$

Свойство (D) (см. выше) буквально верно и в пространстве:
(D) Серединный перпендикуляр к отрезку $AB$ имеет для любой точки $X$ собственность: $\;|XA|=|XB|$ .

Биссектриса [ править ]

Разделение угла пополам с помощью циркуля и линейки.

Биссектриса равных делит угол на два угла . Угол имеет только одну биссектрису. Каждая точка биссектрисы угла равноудалена от сторон угла.

«Внутренняя» или «внутренняя биссектриса» угла — это линия, полупрямая или отрезок, который делит угол меньше 180 ° на два равных угла. «Внешняя» или «внешняя биссектриса» — это линия, которая делит дополнительный угол (180 ° минус исходный угол), образованный одной стороной, образующей исходный угол, и продолжением другой стороны, на два равных угла. ^[1]

Чтобы разделить угол пополам с помощью линейки и циркуля , нужно нарисовать круг, центром которого является вершина. Окружность пересекает угол в двух точках: по одной на каждой ноге. Используя каждую из этих точек в качестве центра, нарисуйте два круга одинакового размера. Пересечение окружностей (двух точек) определяет линию, которая является биссектрисой угла.

Доказательство корректности этой конструкции достаточно интуитивно понятно и опирается на симметрию задачи. Трисекции угла (разделения его на три равные части) невозможно добиться с помощью одного лишь циркуля и линейки (впервые это доказал Пьер Ванцель ).

Внутренняя и внешняя биссектрисы угла перпендикулярны . Если угол образован двумя прямыми, заданными алгебраически как $l_{1}x+m_{1}y+n_{1}=0$ и $l_{2}x+m_{2}y+n_{2}=0,$ тогда внутренняя и внешняя биссектрисы задаются двумя уравнениями ^[2]^{: стр. 15}

{\frac {l_{1}x+m_{1}y+n_{1}}{\sqrt {l_{1}^{2}+m_{1}^{2}}}}=\pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}.

Треугольник [ править ]

Параллелизм и коллинеарность [ править ]

Биссектрисы внутреннего угла треугольника совпадают в точке, называемой инцентром треугольника, как показано на схеме.

Биссектрисы двух внешних углов и биссектриса другого внутреннего угла совпадают. ^[3]^{: стр.149}

Три точки пересечения, каждая из которых представляет собой биссектрису внешнего угла с противоположной расширенной стороной , коллинеарны (падают на одну и ту же прямую). ^[3]^{: с. 149}

Три точки пересечения, две из них между биссектрисой внутреннего угла и противоположной стороной, а третья между биссектрисой другого внешнего угла и продолженной противоположной стороной, лежат на одной прямой. ^[3]^{: с. 149}

Теорема о биссектрисе [ править ]

Теорема о биссектрисе угла касается относительных длин двух сегментов, на которые разделена сторона треугольника линией, делящей противоположный угол пополам. Он приравнивает их относительные длины к относительным длинам двух других сторон треугольника.

Длина [ править ]

Если длины сторон треугольника равны $a,b,c$ , полупериметр $s=(a+b+c)/2,$ а А - угол, противоположный стороне $a$ , то длина внутренней биссектрисы угла A равна ^[3]^{: с. 70}

{\frac {2{\sqrt {bcs(s-a)}}}{b+c}},

или в тригонометрических терминах, ^[4]

{\frac {2bc}{b+c}}\cos {\frac {A}{2}}.

Если внутренняя биссектриса угла А в треугольнике АВС имеет длину $t_{a}$ и если эта биссектриса делит сторону, противоположную А, на отрезки длин m и n , то ^[3]^{: стр.70}

t_{a}^{2}+mn=bc

где b и c — длины сторон, противоположных вершинам B и C; а сторона, противоположная А, делится в пропорции b : c .

Если внутренние биссектрисы углов A, B и C имеют длины $t_{a},t_{b},$ и $t_{c}$ , затем ^[5]

{\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(c+a)^{2}}{ca}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.

Никакие два неконгруэнтных треугольника не имеют одного и того же набора из трех длин биссектрис внутренних углов. ^[6]^[7]

Целочисленные треугольники [ править ]

Существуют целочисленные треугольники с рациональной биссектрисой .

Четырехугольник [ править ]

Внутренние биссектрисы выпуклого четырехугольника либо образуют вписанный четырехугольник (т. е. четыре точки пересечения соседних биссектрис лежат на одной окружности ), ^[8] или они одновременно . В последнем случае четырехугольник является касательным четырехугольником .

Ромб [ править ]

Каждая диагональ ромба делит противоположные углы пополам.

Экстангенциальный четырехугольник [ править ]

Эксцентр эксцентрального четырехугольника лежит на пересечении шести биссектрис. Это биссектрисы внутреннего угла при двух противоположных углах при вершине, биссектрисы внешнего угла (биссектрисы дополнительных углов) при двух других углах при вершине и биссектрисы внешнего угла при углах, образующихся при пересечении продолжений противоположных сторон .

Парабола [ править ]

Касательная к параболе перпендикулярной в любой точке делит пополам угол между линией, соединяющей точку с фокусом, и линией, идущей от точки и директрисе .

Биссектрисы сторон многоугольника [ править ]

Треугольник [ править ]

Медианы [ править ]

Каждая из трех медиан треугольника представляет собой отрезок, проходящий через одну вершину и середину противоположной стороны, поэтому он делит эту сторону пополам (хотя, как правило, не перпендикулярно). Три медианы пересекаются друг с другом в точке, называемой центроидом треугольника , которая является его центром масс, если он имеет однородную плотность; таким образом, любая линия, проходящая через центр тяжести треугольника и одну из его вершин, делит противоположную сторону пополам. Центр тяжести находится в два раза ближе к середине любой стороны, чем к противоположной вершине.

Биссектрисы [ править ]

Внутренний перпендикуляр, биссектриса стороны треугольника — это отрезок, полностью попадающий на треугольник и внутри него, линии, которая перпендикулярно делит эту сторону пополам. Три биссектрисы трех сторон треугольника пересекаются в центре описанной окружности (центре окружности, проходящей через три вершины). Таким образом, любая линия, проходящая через центр окружности треугольника и перпендикулярная стороне, делит эту сторону пополам.

В остроугольном треугольнике центр описанной окружности делит внутренние серединные перпендикуляры двух кратчайших сторон в равных пропорциях. В тупоугольном треугольнике серединные перпендикуляры двух кратчайших сторон (выходящие за пределы противоположных сторон треугольника до центра описанной окружности) делятся на соответствующие пересекающиеся стороны треугольника в равных пропорциях. ^[9]^{: Следствия 5 и 6.}

Для любого треугольника внутренние серединные перпендикуляры определяются выражением $p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},$ $p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},$ и $p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}},$ где стороны $a\geq b\geq c$ и площадь $T.$ ^[9]^{: Вопрос 2}

Четырехугольник [ править ]

Две бимедианы выпуклого . четырехугольника — это отрезки, которые соединяют середины противоположных сторон и, следовательно, делят пополам две стороны Две бимедианы и отрезок, соединяющий середины диагоналей, совпадают в точке, называемой «центроидом вершины», и все делятся этой точкой пополам. ^[10]^{: стр. 125}

Четыре «высоты» выпуклого четырехугольника представляют собой перпендикуляры к стороне, проходящие через середину противоположной стороны, следовательно, делящие последнюю сторону пополам. Если четырехугольник циклический (вписан в круг), эти степени совпадают (все встречаются в) в общей точке, называемой «антицентром».

Теорема Брахмагупты утверждает, что если вписанный четырехугольник ортодиагонален (то есть имеет перпендикулярные диагонали ), то перпендикуляр к стороне, проходящей из точки пересечения диагоналей, всегда делит противоположную сторону пополам.

Конструкция серединного перпендикуляра образует четырехугольник из серединных перпендикуляров сторон другого четырехугольника.

площади и периметра Биссектрисы биссектрисы

Треугольник [ править ]

Существует бесконечное количество линий, делящих площадь треугольника пополам . Три из них являются медианами треугольника (которые соединяют середины сторон с противоположными вершинами), и они совпадают треугольника в центроиде ; действительно, это единственные биссектрисы площади, проходящие через центр тяжести. Три другие биссектрисы параллельны сторонам треугольника; каждая из них пересекает две другие стороны так, чтобы разделить их на сегменты с пропорциями ${\sqrt {2}}+1:1$ . ^[11] Эти шесть линий совпадают по три одновременно: помимо того, что три медианы совпадают, любая медиана совпадает с двумя биссектрисами параллельной площади.

Огибающая (в широком смысле определяемый как фигура с тремя вершинами, соединенными кривыми , бесконечности биссектрис представляет собой дельтоид вогнутыми к внешней стороне дельтоиды, что делает внутренние точки невыпуклым множеством). ^[11] Вершины дельтовидных мышц находятся на серединах медиан; все точки внутри дельтовидной мышцы находятся на трех разных биссектрисах, а все точки за ее пределами - только на одной. [1] Стороны дельтоида представляют собой дуги гипербол расширенным , асимптотические сторонам треугольника. ^[11] Отношение площади огибающей биссектрис к площади треугольника инвариантно для всех треугольников и равно ${\tfrac {3}{4}}\log _{e}(2)-{\tfrac {1}{2}},$ т.е. 0,019860... или менее 2%.

Кливер треугольника — это отрезок, который делит периметр треугольника пополам и имеет одну конечную точку в середине одной из трех сторон. Три скалывателя совпадают (все проходят через) в центре круга Шпикера , который является вписанной окружностью медиального треугольника . Кливеры параллельны биссектрисам угла.

Разветвитель треугольника — это отрезок линии, имеющий одну конечную точку в одной из трех вершин треугольника и делящий периметр пополам. Три разделителя совпадают в точке Нагеля треугольника.

Любая линия, проходящая через треугольник, которая делит площадь треугольника и его периметр пополам, проходит через центр треугольника (центр вписанной окружности ) . В любом треугольнике их может быть один, два или три. Линия, проходящая через центр, делит пополам одну область или периметр тогда и только тогда, когда она также делит пополам другую. ^[12]

Параллелограмм [ править ]

Любая прямая, проходящая через середину параллелограмма , делит площадь пополам. ^[11] и периметр.

Круг и эллипс [ править ]

Все биссектрисы площади и биссектрисы периметра круга или другого эллипса проходят через центр , а любые хорды, проходящие через центр, делят площадь и периметр пополам. В случае круга это диаметры круга.

Биссектрисы диагоналей [ править ]

Параллелограмм [ править ]

Диагонали . параллелограмма делят друг друга пополам

Четырехугольник [ править ]

Если отрезок, соединяющий диагонали четырехугольника, делит обе диагонали пополам, то этот отрезок ( линия Ньютона ) сам делится пополам центроидом вершины.

Биссектрисы объёма [ править ]

Плоскость, разделяющая два противоположных ребра тетраэдра в заданном соотношении, в том же отношении делит и объем тетраэдра. Таким образом, любая плоскость, содержащая бимедиану (соединитель середин противоположных ребер) тетраэдра, делит объем тетраэдра пополам. ^[13]^[14]^{: стр.89–90.}

Ссылки [ править ]

^ Вайсштейн, Эрик В. «Биссектриса внешнего угла». Из MathWorld — веб-ресурса Wolfram.
^ Испания, Барри. Аналитическая коника , Dover Publications, 2007 г. (оригинал 1957 г.).
^ Jump up to: ^а ^б ^с ^д ^и Джонсон, Роджер А., Расширенная евклидова геометрия , Dover Publ., 2007 (исходник: 1929).
^ Оксман, Виктор. «О существовании треугольников с заданными длинами одной стороны и двух смежных биссектрис», Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
^ Саймонс, Стюарт. Математический вестник 93, март 2009 г., стр. 115–116.
^ Миронеску П. и Панайтополь Л., «Существование треугольника с заданной длиной биссектрисы», American Mathematical Monthly 101 (1994): 58–60.
^ Оксман, Виктор, «Чисто геометрическое доказательство уникальности треугольника с предписанными биссектрисами», Forum Geometricorum 8 (2008): 197–200.
^ Вайсштейн, Эрик В. «Четырехугольник». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Quadri Lateral.html
^ Jump up to: ^а ^б Митчелл, Дуглас В. (2013), «Биссектрисы сторон треугольника», Forum Geometricorum 13, 53–59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
^ Альтшиллер-Корт, Натан, Геометрия колледжа , Dover Publ., 2007.
^ Jump up to: ^а ^б ^с ^д Данн, Джас. А.; Красиво, Джас. Э. (май 1972 г.). «Разделение треугольника пополам». Математический вестник . 56 (396): 105–108. дои : 10.2307/3615256 . JSTOR 3615256 .
^ Кодокостас, Димитриос, «Треугольные эквалайзеры», журнал Mathematics Magazine 83, апрель 2010 г., стр. 141–146.
^ Вайсштейн, Эрик В. «Тетраэдр». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Tetrahedron.html
^ Альтшиллер-Корт, Н. «Тетраэдр». Ч. 4 в «Современной чистой твердой геометрии» : Челси, 1979.

Внешние ссылки [ править ]

Биссектриса разрезанного узла
Определение биссектрисы угла. Открытый справочник по математике с интерактивным апплетом
Определение биссектрисы. Открытый справочник по математике с интерактивным апплетом
Биссектриса перпендикуляра. С интерактивным апплетом
Анимированные инструкции по разделению угла и линии пополам с помощью циркуля и линейки.
Вайсштейн, Эрик В. «Биссектриса» . Математический мир .

Эта статья включает в себя материал из биссектрисы угла на сайте PlanetMath , который доступен под лицензией Creative Commons Attribution/Share-Alike License .

[1] Вайсштейн, Эрик В. «Биссектриса внешнего угла». Из MathWorld — веб-ресурса Wolfram.

[2] Испания, Барри. Аналитическая коника , Dover Publications, 2007 г. (оригинал 1957 г.).

[Johnson-3] Jump up to: ^а ^б ^с ^д ^и Джонсон, Роджер А., Расширенная евклидова геометрия , Dover Publ., 2007 (исходник: 1929).

[4] Оксман, Виктор. «О существовании треугольников с заданными длинами одной стороны и двух смежных биссектрис», Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf

[5] Саймонс, Стюарт. Математический вестник 93, март 2009 г., стр. 115–116.

[6] Миронеску П. и Панайтополь Л., «Существование треугольника с заданной длиной биссектрисы», American Mathematical Monthly 101 (1994): 58–60.

[7] Оксман, Виктор, «Чисто геометрическое доказательство уникальности треугольника с предписанными биссектрисами», Forum Geometricorum 8 (2008): 197–200.

[8] Вайсштейн, Эрик В. «Четырехугольник». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Quadri Lateral.html

[Mitchell-9] Jump up to: ^а ^б Митчелл, Дуглас В. (2013), «Биссектрисы сторон треугольника», Forum Geometricorum 13, 53–59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf

[Altshiller-Court-10] Альтшиллер-Корт, Натан, Геометрия колледжа , Dover Publ., 2007.

[Dunn-11] Jump up to: ^а ^б ^с ^д Данн, Джас. А.; Красиво, Джас. Э. (май 1972 г.). «Разделение треугольника пополам». Математический вестник . 56 (396): 105–108. дои : 10.2307/3615256 . JSTOR 3615256 .

[12] Кодокостас, Димитриос, «Треугольные эквалайзеры», журнал Mathematics Magazine 83, апрель 2010 г., стр. 141–146.

[13] Вайсштейн, Эрик В. «Тетраэдр». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Tetrahedron.html

[14] Альтшиллер-Корт, Н. «Тетраэдр». Ч. 4 в «Современной чистой твердой геометрии» : Челси, 1979.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]